Number all real numbers on the interval [0,1]
As a proof of the uncountable real numbers in all textbooks on set theory, the so-called Cantor diagonal method is given (for more details, see the book “What is Mathematics?” By Courant, Robbins, §4. Mathematical analysis of the infinite. 2. uncountable
continuum.). This method proves the uncountability of a subset of real numbers belonging to the range [0,1]. However, if you look at the evidence, it becomes clear that it does not take into account the exponential growth of possible options with each increment of the serial number in decimal.
The cantor argues as follows (but only with respect to infinite decimal fractions): we place the decimal fractions in an arbitrary manner in the form of a list, then we number them and consider the diagonal. If we add 1 to each digit on the diagonal, we will get a number that is not in this list. This moment at the intuitive level is doubtful.
In order to understand what this is about, let's try to consider the idea of a diagonal method using the following example. Consider the final fractions of the form: 0, a 1 a 2 a 3 a 4 a 5 , we form a list of them so that we get a square of 5 * 5 in size, as shown in the figure below:

')
Let's apply the Cantor method, and indeed, the number 0,22226 is not in this square. But, it is in the rectangle 5 * n 5 , where 5 is the number of decimal places, and n is the number of digits in the calculus system used (in this example, n = 10). This is explained by the fact that the number of combinations of all possible fractions, the length of which is 5 decimal places, is n 5 .
Letting the size of the square go to infinity, we get what is called the Cantor diagonal method . But at infinity you need to direct not a square, but a rectangle of size m * n m , where m is the number of positions after the comma, m -> ∞.
To number all real numbers belonging to the range [0, 1], they must be arranged in the form of an exponentially growing tree. Consider the decimal fractions written in binary . Let k - the number of decimal places, n - the size of the alphabet of a number system. Then the number of possible variants of fractions starting with k = 1 and up to ∞ will be a function of k, it can be seen in the figure below:
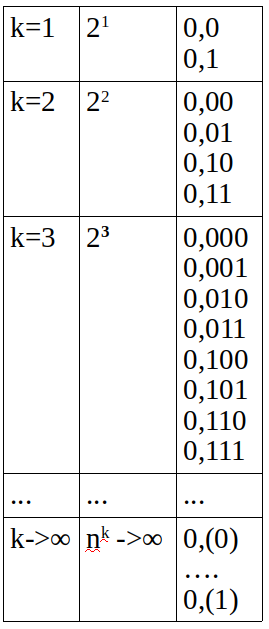
Let's call each row in the above table a level . Thus, k is both the level number and the number of decimal places at the same time.
We introduce two sequence numbers:
We represent all binary decimal fractions in the form of a binary tree, as in the table below:

Each individual digit in the decimal position is located in a separate cell. In front of each such digit, we write 2 indices C and L as follows: N C L, where N is the value of the digit.
It becomes obvious that C and L are functions of k and the digits of the number N itself: C = fC (k; N), L = fL (k; N). It also becomes obvious that we can number all the numbers from the range [0,1], since we successively go through each level and successively number all possible combinations at this level.
It remains to derive an analytical dependence for the counters C = f C (N) and L = f L (k; N).
For convenience, we denote L (k; N) as L k .
We assume that L 0 - 1 = 0.
If you carefully study the table, the following pattern emerges:
L k = (L k-1 - 1) * S + N + 1,
where k> = 1, N is the current digit in the fraction, S = | {0,1} | = 2 - the size of the alphabet of the binary number system. Record | A | means the power of the set A, for a finite set is the number of elements in it.
Obviously, C contains the sum of all combinations for all previous levels plus L numbers for the current level, i.e. C (N) = Σ i∈ [1, k-1] 2 i + L (k; N).
Consider an arbitrary number 0, 0101 . Its serial number is C (0,0101) = 2 1 + 2 2 + 2 3 + L 4 = 2 + 4 + 8 + 6 = 20.
Calculations:
L 1 = (L 0 -1) * 2 + 0 + 1 = 0 * 2 + 0 + 1 = 1
L 2 = (L 1 - 1) * 2 + 1 + 1 = (1 - 1) * 2 + 1 + 1 = 2
L 3 = (L 2 - 1) * 2 + 0 + 1 = (2 - 1) * 2 + 0 + 1 = 3
L 4 = (L 3 - 1) * 2 + 1 + 1 = (3 - 1) * 2 + 1 + 1 = 6
Visualization:

Consider an arbitrary number 0, 1001 . Its serial number is C (0.1001) = 2 1 + 2 2 + 2 3 + L 4 = 2 + 4 + 8 + 10 = 24.
L 1 = (L 0 - 1) * 2 + 1 + 1 = 0 * 2 + 1 + 1 = 2
L 2 = (L 1 - 1) * 2 + 0 + 1 = (1 - 1) * 2 + 0 + 1 = 3
L 3 = (L 2 - 1) * 2 + 0 + 1 = (2 - 1) * 2 + 0 + 1 = 5
L 4 = (L 3 - 1) * 2 + 1 + 1 = (3 - 1) * 2 + 1 + 1 = 10
Visualization:

Thus, we obtained an algorithm that sequentially numbers absolutely all real numbers from the range [0, 1], and if we take an arbitrary decimal fraction of arbitrary length, then we can calculate its unique spin number.
PS If the algorithm proposed by me has an error that I, because of my carelessness, do not see - a big request to write about it in the comments.
PPS If there is no error, it turns out that | [0,1] | = | N |! Those. ALL real numbers from the range [0,1] can be numbered!
continuum.). This method proves the uncountability of a subset of real numbers belonging to the range [0,1]. However, if you look at the evidence, it becomes clear that it does not take into account the exponential growth of possible options with each increment of the serial number in decimal.
The cantor argues as follows (but only with respect to infinite decimal fractions): we place the decimal fractions in an arbitrary manner in the form of a list, then we number them and consider the diagonal. If we add 1 to each digit on the diagonal, we will get a number that is not in this list. This moment at the intuitive level is doubtful.
Lack of diagonal method
In order to understand what this is about, let's try to consider the idea of a diagonal method using the following example. Consider the final fractions of the form: 0, a 1 a 2 a 3 a 4 a 5 , we form a list of them so that we get a square of 5 * 5 in size, as shown in the figure below:

')
Let's apply the Cantor method, and indeed, the number 0,22226 is not in this square. But, it is in the rectangle 5 * n 5 , where 5 is the number of decimal places, and n is the number of digits in the calculus system used (in this example, n = 10). This is explained by the fact that the number of combinations of all possible fractions, the length of which is 5 decimal places, is n 5 .
Letting the size of the square go to infinity, we get what is called the Cantor diagonal method . But at infinity you need to direct not a square, but a rectangle of size m * n m , where m is the number of positions after the comma, m -> ∞.
Idea of my approach
To number all real numbers belonging to the range [0, 1], they must be arranged in the form of an exponentially growing tree. Consider the decimal fractions written in binary . Let k - the number of decimal places, n - the size of the alphabet of a number system. Then the number of possible variants of fractions starting with k = 1 and up to ∞ will be a function of k, it can be seen in the figure below:

Let's call each row in the above table a level . Thus, k is both the level number and the number of decimal places at the same time.
We introduce two sequence numbers:
- common counter ( C , Counter), used for sequential numbering of all numbers from the range [0,1];
- level counter ( L , per Level counter), used to number the numbers at each level separately, reset to the next level. For the first level, L will take the values 1 and 2, for the second - 1, 2, 3 and 4, etc.
We represent all binary decimal fractions in the form of a binary tree, as in the table below:

Each individual digit in the decimal position is located in a separate cell. In front of each such digit, we write 2 indices C and L as follows: N C L, where N is the value of the digit.
It becomes obvious that C and L are functions of k and the digits of the number N itself: C = fC (k; N), L = fL (k; N). It also becomes obvious that we can number all the numbers from the range [0,1], since we successively go through each level and successively number all possible combinations at this level.
It remains to derive an analytical dependence for the counters C = f C (N) and L = f L (k; N).
For convenience, we denote L (k; N) as L k .
We assume that L 0 - 1 = 0.
If you carefully study the table, the following pattern emerges:
L k = (L k-1 - 1) * S + N + 1,
where k> = 1, N is the current digit in the fraction, S = | {0,1} | = 2 - the size of the alphabet of the binary number system. Record | A | means the power of the set A, for a finite set is the number of elements in it.
Obviously, C contains the sum of all combinations for all previous levels plus L numbers for the current level, i.e. C (N) = Σ i∈ [1, k-1] 2 i + L (k; N).
Examples
Consider an arbitrary number 0, 0101 . Its serial number is C (0,0101) = 2 1 + 2 2 + 2 3 + L 4 = 2 + 4 + 8 + 6 = 20.
Calculations:
L 1 = (L 0 -1) * 2 + 0 + 1 = 0 * 2 + 0 + 1 = 1
L 2 = (L 1 - 1) * 2 + 1 + 1 = (1 - 1) * 2 + 1 + 1 = 2
L 3 = (L 2 - 1) * 2 + 0 + 1 = (2 - 1) * 2 + 0 + 1 = 3
L 4 = (L 3 - 1) * 2 + 1 + 1 = (3 - 1) * 2 + 1 + 1 = 6
Visualization:

Consider an arbitrary number 0, 1001 . Its serial number is C (0.1001) = 2 1 + 2 2 + 2 3 + L 4 = 2 + 4 + 8 + 10 = 24.
L 1 = (L 0 - 1) * 2 + 1 + 1 = 0 * 2 + 1 + 1 = 2
L 2 = (L 1 - 1) * 2 + 0 + 1 = (1 - 1) * 2 + 0 + 1 = 3
L 3 = (L 2 - 1) * 2 + 0 + 1 = (2 - 1) * 2 + 0 + 1 = 5
L 4 = (L 3 - 1) * 2 + 1 + 1 = (3 - 1) * 2 + 1 + 1 = 10
Visualization:

findings
Thus, we obtained an algorithm that sequentially numbers absolutely all real numbers from the range [0, 1], and if we take an arbitrary decimal fraction of arbitrary length, then we can calculate its unique spin number.
PS If the algorithm proposed by me has an error that I, because of my carelessness, do not see - a big request to write about it in the comments.
PPS If there is no error, it turns out that | [0,1] | = | N |! Those. ALL real numbers from the range [0,1] can be numbered!
Source: https://habr.com/ru/post/358526/
All Articles