Natural Motion Simulation: Steering Behaviors
Steering behaviors help autonomous characters to move realistically through the use of simple forces, the combination of which creates a natural-looking and improvised movement around the environment. In this tutorial, I will talk about the basics of the theory of steering behaviors, as well as their implementation.
The ideas on which such behaviors are built are proposed by Craig Reindolds ; they are not based on complex strategies using path planning or global computing, but use local information, such as the strength of neighboring objects. Because of this, they are easy to understand and implement, but at the same time capable of creating very complex patterns of movement.
Note: although this tutorial was written in AS3 and Flash, the same techniques and concepts can be used in almost any game development environment. You will need a basic understanding of math vectors.
Part 1. Behavior Seek (search)
Position, speed and movement
Realization of all forces involved in steering behaviors is possible using mathematical vectors. Since these forces affect the speed and position of the character, it will also be logical to use vectors to represent them.
')
Although the vector has a direction , we will ignore it when it comes to the position (we assume that the position vector indicates the character’s current location).

The image above shows a character in
(x, y) and having speed (a, b) . Motion is calculated using the Euler method : position = position + velocity The direction of the velocity vector will control the direction of movement of the character, and its length (or value) will control the amount of movement for each frame. The greater the length, the faster the character moves. The velocity vector can be truncated so that it does not exceed a certain value (usually this is the maximum speed). The image below shows this approach.
Red square moves towards the goal. The motion pattern illustrates the behavior of seek , but so far without control forces applied. The green line indicates the velocity vector, calculated as follows:
velocity = normalize(target - position) * max_velocity It is important to note that without a controlling force, the character describes the direct routes and instantly changes its direction as the target moves, thus making a sharp transition between the current and the new routes.
Force calculation
If only the force of speed is involved, the character will move only in a straight line defined by the direction of this vector. One of the principles of steering behaviors is to influence the movement of the character by adding forces (called controlling forces ). Thanks to these forces, the character will move in one direction or another.
In the case of seek behavior, adding a character in each frame of control forces causes him to smoothly change speed, avoiding abrupt changes of route. If the target moves, the character will gradually change its speed vector, trying to reach the target in its new location.
Two forces are involved in the seek behavior: the required speed and the controlling force:
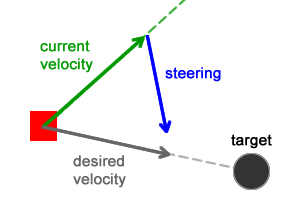
The required speed is the force directing the character to the target along the shortest possible path (in a straight line between them - previously it was the only force acting on the character). The control force is the result of subtracting the current speed from the desired speed; she also directs the character to the goal.
These forces are calculated as follows:
desired_velocity = normalize(target - position) * max_velocity steering = desired_velocity - velocity Force application
After calculating the control force, it must be applied to the character (it will be added to the force of speed). The frame-by-frame addition of the control force to the speed causes the character to smoothly leave the old straight route and head towards the target, describing the search trajectory (the orange curve in the figure below):

The application of these forces and the calculation of the final velocity / position are as follows:
steering = truncate (steering, max_force) steering = steering / mass velocity = truncate (velocity + steering , max_speed) position = position + velocity The control force is truncated so that it cannot exceed the amount of permissible forces that the character can handle. In addition, the control force is divided by the mass of the character, which creates different speeds for characters with different weights.
Each time the target moves, the vector of the required speed of each character changes accordingly. However, the change in the velocity vector and the fact that he again pointed to the target, takes some time. The result is smooth motion transitions.
Part 2. Flee and Arrival Conduct
Runaway
The behavior of seek described above is based on two forces that guide the character to the goal: the required speed and control force.
desired_velocity = normalize(target - position) * max_velocity steering = desired_velocity - velocity In this case,
desired_velocity is the shortest path between the character and the target. It is obtained by subtracting the position of the target from the position of the character. The result is a force vector passing from the character to the target .
In the behavior of the flee, the same two forces are used, but they are configured so that the character runs away from the target:

Flee Behavior
This new
desired_velocity vector desired_velocity calculated by subtracting the character 's position from the target's position, which gives us a vector directed from the target to the character .The resulting strengths are calculated almost the same as in seek behavior:
desired_velocity = normalize(position - target) * max_velocity steering = desired_velocity - velocity In this case,
desired_velocity represents the shortest escape route that a character can use to get away from the goal. The controlling force causes the character to leave the current route, pushing it in the direction of the vector of the desired speed.When comparing the vector of the required speed in the behavior of flee with the same vector in the behavior of seek, we can derive the following relationship:
flee_desired_velocity = -seek_desired_velocity In other words, one vector is negative with respect to the other.
Application of avoidance forces
After calculating the control force, it must be added to the character's velocity vector. Since this force pushes the character away from the target, the character will no longer move to the target in each frame and will move away from it, creating an escape trajectory (the orange curve in the figure below):
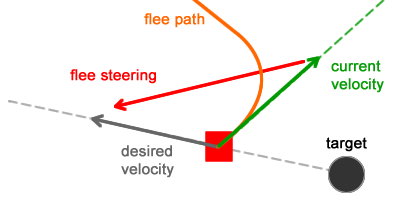
The addition of these forces and the calculation of the final speeds / positions are performed in the same way as before.
The application of all forces forces each character to smoothly leave the current route and avoid the goal.
While the goal affects each character, not taking into account the distance between them; You can limit its "area of influence", so that the character runs away only if it is too close to the goal.
Arrival
As we have seen, the behavior of seek makes the character move towards the goal. When he reaches his goal, the control force continues to act on him in accordance with the same rules, causing the character to “bounce” back and forth around the target.
The arrival behavior does not allow the character to move through the target. When approaching the end point, it causes the character to slow down and stop when it reaches the goal.
This behavior consists of two stages. The first stage is when the character is far from the goal; it works just like the behavior of seek (the character at full speed moves to the goal).
The second stage begins when the character is close to the target, is inside its “slowdown area” (a circle centered at the target location):
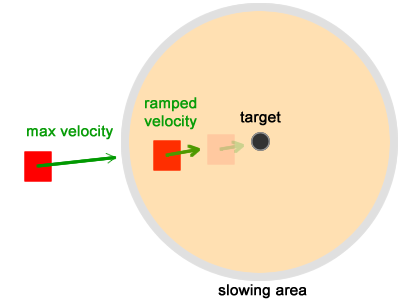
When a character enters a circle, he slows down until he stops at the target.
Slowdown
When a character enters a slowdown area, his speed drops linearly to zero. This can be achieved by applying a new control force ( arrival force ) to the character's velocity vector. The result of this addition will sooner or later be equal to zero, that is, in every frame nothing will be added to the character’s position (that is, there will be no movement):
// (velocity + steering) , velocity = truncate(velocity + steering, max_speed) position = position + velocity function truncate(vector:Vector3D, max:Number) :void { var i :Number; i = max / vector.length; i = i < 1.0 ? i : 1.0; vector.scaleBy(i); } To slow down the character before stopping, the speed should not instantly drop to zero. The process of gradual deceleration is calculated based on the radius of the deceleration area and the distance between the character and the target:
// desired_velocity = target - position distance = length(desired_velocity) // , // if (distance < slowingRadius) { // desired_velocity = normalize(desired_velocity) * max_velocity * (distance / slowingRadius) } else { // desired_velocity = normalize(desired_velocity) * max_velocity } // steering = desired_velocity - velocity If the distance is greater than
slowingRadius , then the character is far from the target and his speed should remain equal to max_velocity .If the distance is less than
slowingRadius , then the character entered the area of slowing down and his speed should decrease.The value of
distance / slowingRadius varies from 1 (when distance is slowingRadius ) to 0 (when distance almost zero). A linear change causes the speed to decrease smoothly: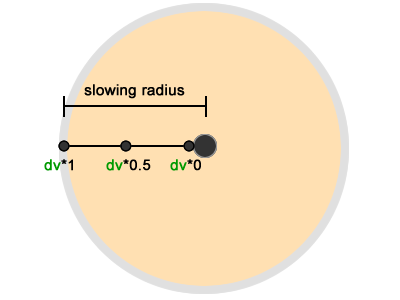
As stated above, character movement is as follows:
steering = desired_velocity - velocity velocity = truncate (velocity + steering , max_speed) position = position + velocity If the required speed is reduced to zero, then the control force becomes equal to
-velocity . Therefore, when this control force is added to the speed, we get a zero, which causes the character to stop.Essentially, the arrival behavior computes a force that must be equal to
-velocity , not allowing the character to move while this force is applied. The original velocity vector of the character does not change and continues to work, but is reset by the addition of the control force.If the arrival control power is removed, the character starts moving again using the original velocity vector.
Conclusion
The behavior of the flee makes the character move away from the target, and the behavior of the arrival causes him to slow down and stop at the target position. Both behaviors can be used to create smooth runaway or follow patterns. In addition, they can be combined to create even more complex movements.
Part 3. Behavior Wander
Wandering
In games, it is often necessary that characters randomly wander around their surroundings. Usually such characters are just waiting for some event (for example, a fight with a player) or are looking for something. When a player is able to see this behavior, the function of the character wandering should be quite realistic and beautiful looking.
If the player sees clearly defined routes or unrealistic movements, this will lead to irritation. In the worst case, the player will understand how to predict the movement of the character, and then the gameplay will become boring for him.
The wander control behavior is designed to create a realistic “natural” movement that will convince the player that the character is actually alive and walking independently.
Search and accident
There are several ways to implement a wandering pattern using steering behaviors. The simplest is the previously described seek behavior. When a character performs a search, he moves to the goal.
If the position of this goal changes every few seconds, the character will never be able to achieve it (and if they can, the goal will move again). If we place the goal in the game area at random, the character will move around the environment, pursuing the goal.
Flash online demo is here .
You can implement this with the following code:
// private function wander() :Vector3D { var now :Number = (new Date()).getTime(); if (now >= nextDecision) { // "" } // , // ( seek) return seek(target); } // // , : public function update() :void { steering = wander() steering = truncate (steering, max_force) steering = steering / mass velocity = truncate (velocity + steering , max_speed) position = position + velocity } This is a simple and good approach, but its end result does not look quite believable. Sometimes a character completely changes his route, because the target is placed behind his back. Then the character's behavior is more perceived as "Damn, I forgot the keys!" , And not "So, now I will go in this direction . "
Wandering
Another implementation of the wander behavior was proposed by Craig Reynolds when he invented these behaviors. The main idea is to create small random shifts and attach them in each game frame to the vector of the current direction of the character (in our case, to speed). Since the velocity vector determines the direction of movement of the character and the speed of his movement, any impact on this vector will lead to a change in the current route.
The use of small offsets in each frame allows you to avoid abrupt changes in the character's route. For example, if a character moves up and turns to the right, then in the next frame of the game he will still move up and turn to the right, but slightly from a different angle.
This approach can also be implemented in different ways. One of them is to place a circle in front of the character and use it to calculate all the influencing forces:

The starting point of the displacement force is in the center of the circle and is limited by its radius. The greater the radius and distance from the character to the circle, the stronger the impulse received by the player in each frame of the game.
This bias force will be used to influence the character’s route. It is used to calculate the power of the wander .
Calculation of the position of the circle
The first component needed to calculate the wandering power is the position of the center of the circle. Since the circle must be placed in front of the character, the velocity vector can be used as a guide:
// CIRCLE_DISTANCE - // , - . // : var circleCenter :Vector3D; circleCenter = velocity.clone(); circleCenter.normalize(); circleCenter.scaleBy(CIRCLE_DISTANCE); The
circleCenter vector is a clone (copy) of the velocity vector, that is, it points in the same direction. It is normalized and multiplied by the scalar value (in our case, CIRCLE_DISTANCE ), which will give us the following vector: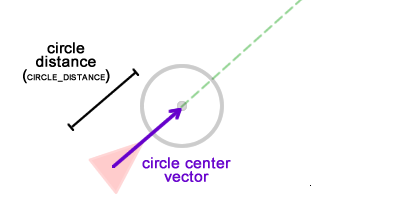
Displacement force
The next component is the bias force responsible for turning left and right. Since this force is used to create deviations, it can be sent anywhere. Let's use a vector aligned with the Y axis:
var displacement :Vector3D; displacement = new Vector3D(0, -1); displacement.scaleBy(CIRCLE_RADIUS); // // // setAngle(displacement, wanderAngle); // // wanderAngle, // // . wanderAngle += (Math.random() * ANGLE_CHANGE) - (ANGLE_CHANGE * .5); The offset force is created and scaled by the radius of the circle. As stated above, the larger the radius, the stronger the power of the walk.
wanderAngle is a scalar value that determines the amount of “slope” of the bias force; after using it, a random value is added to it, so that in the next frame of the game it will be different. This creates the necessary randomness in motion.To understand this, let's imagine that the offset force calculated above is located in the center of the circle. Since it is scaled to the radius of a circle, it will look something like this:

Hint: do not forget that mathematical vectors do not have a position in space, they only have a direction and a magnitude (length). Therefore, they can be located anywhere.
Power of wandering
After calculating the center of the circle and the displacement vector, they must be connected to get the strength of the walk . This force is calculated by adding these two vectors:
var wanderForce :Vector3D; wanderForce = circleCenter.add(displacement); Visually, we can imagine these forces as follows:
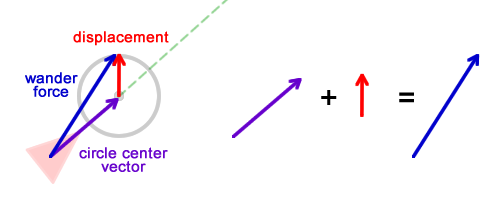
The power of wandering can be represented as a vector, emanating from the character to a point on the circle circumference. Depending on the location of this point, the wandering power will push the character left or right, strongly or weakly:
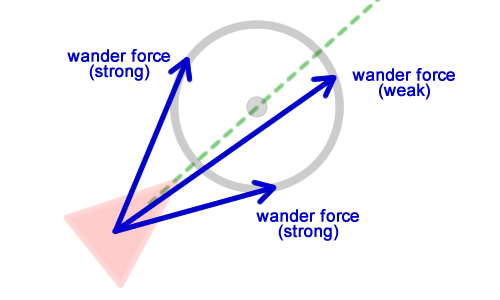
The more the power of the walk is aligned with the velocity vector, the less the character will change the current route. The wandering power will act exactly like the seek and flee powers: it will push the character in the right direction.
Just as the direction of force in the seek and flee behaviors is calculated based on the target, the wandering direction is calculated based on a random point on the circle of the circle. The final code for the wandering power is:
private function wander() :Vector3D { // var circleCenter :Vector3D; circleCenter = velocity.clone(); circleCenter.normalize(); circleCenter.scaleBy(CIRCLE_DISTANCE); // // var displacement :Vector3D; displacement = new Vector3D(0, -1); displacement.scaleBy(CIRCLE_RADIUS); // // // setAngle(displacement, wanderAngle); // // wanderAngle, // // . wanderAngle += Math.random() * ANGLE_CHANGE - ANGLE_CHANGE * .5; // // var wanderForce :Vector3D; wanderForce = circleCenter.add(displacement); return wanderForce; } public function setAngle(vector :Vector3D, value:Number):void { var len :Number = vector.length; vector.x = Math.cos(value) * len; vector.y = Math.sin(value) * len; } Bonding
After calculating the power of wandering, it must be added to the character’s speed so that she can influence his movement. The addition of this force is exactly the same as before:
steering = wander() steering = truncate (steering, max_force) steering = steering / mass velocity = truncate (velocity + steering , max_speed) position = position + velocity The power of wandering will affect the character’s route in the same way as the behaviors described above. The difference is that in every frame of the game, it pushes the character in a random direction.
Flash online demo is here .
Conclusion
Behavior Wander - a great way to implement random movement. It is driven by an imaginary circle located in front of the character, which can be changed to create the necessary pattern of movement.
Part 4. Pursuit and Evade
What is pursuit?
Pursuit (pursuit) - the process of following the goal with the desire to catch it . It is important to note that all the difference here is the word "catch." If the object simply follows the target, then it is enough for it to repeat the movement of the target, therefore, it will follow its tracks.
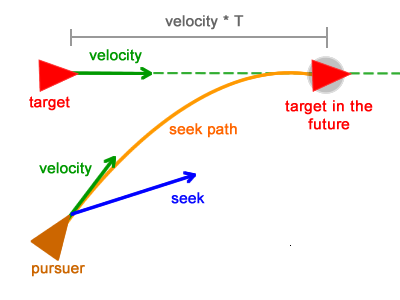
When pursuing someone, the pursuer should follow the goal, but also predict where the goal will be in the near future. If we can predict (or estimate) where the target will be in the next few seconds, we will be able to change the current trajectory to avoid unnecessary routes:
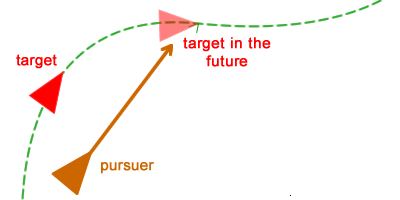
Future forecasting
As stated in the first part of the tutorial, the motion is calculated using the Euler method :
position = position + velocity From this it follows directly that if the character’s current position and speed are known, then we can predict where he will be through
T game updates. Suppose a character moves in a straight line and the position we want to predict is located after three updates ( T=3 ). Then the character’s future position will be: position = position + velocity * T For correct prediction, you must select the correct value of
T If the value is too large, the pursuer will chase the ghost. If T too close to zero, then the pursuer does not really pursue, but simply follows the target (no prediction).If the forecast is calculated for each frame of the game, then it will work, even if the goal is constantly changing its direction. With each update, a new “future position” is generated, based on the character’s current speed vector (which also controls the direction of movement).
Pursuing
The behavior of Pursuit works about the same as Seek; the only difference is that the pursuer is not striving for the goal itself, but for its position in the near future.
Suppose all the characters in the game are represented by a class
Boid. Then in the following pseudocode, the basic idea of pursuit behavior is implemented: public function pursuit(t :Boid) :Vector3D { T :int = 3; futurePosition :Vector3D = t.position + t.velocity * T; return seek(futurePosition); } After calculating the power of pursuit, it must be added to the velocity vector, as in all previous control forces:
public function update() :void { steering = pursuit(target) steering = truncate (steering, max_force) steering = steering / mass velocity = truncate (velocity + steering , max_speed) position = position + velocity } The figure below shows this process:

The pursuer (the character below) tends to the future position of the target, following the trajectory described by the orange curve. The finished result is shown below. Here pursuit behavior is used
T=30.Interactive Flash demo is here .
Improve prosecution accuracy
T , : . , , , T «»., , .
, . :
T : T = distanceBetweenTargetAndPursuer / MAX_VELOCITY The new value is
Tcalculated based on the distance between the two characters and the maximum speed that the target can reach. Simply put, a new one Tmeans “how many updates does a target need to move from the current position to the pursuer position” .The greater the distance, the greater will be
T, that is, the pursuer will tend to a point far ahead of the goal. The shorter the distance, the smaller it will be T, that is, it will tend to a point that is very close to the target. The new code for this implementation will look like this: public function pursuit(t :Boid) :Vector3D { var distance :Vector3D = t.position - position; var T :int = distance.length / MAX_VELOCITY; futurePosition :Vector3D = t.position + t.velocity * T; return seek(futurePosition); } Behavior Pursuit uses dynamic
T.Flash online demo is here .
Evading
Evade Pursuit. Evade :

, :
public function evade(t :Boid) :Vector3D { var distance :Vector3D = t.position - position; var updatesAhead :int = distance.length / MAX_VELOCITY; futurePosition :Vector3D = t.position + t.velocity * updatesAhead; return flee(futurePosition); } Flash .
Conclusion
Pursuit Evade, , , , .
5.
Steering behaviors , , , . .
Steering Forces
, steering behavior ( « »), . , (seek, flee, wander ). :
steering = seek(); // steering = truncate (steering, max_force) steering = steering / mass velocity = truncate (velocity + steering , max_speed) position = position + velocity , ( , ). «» , . :
steering = nothing(); // , " " steering = steering + seek(); steering = steering + flee(); (...) steering = truncate (steering, max_force) steering = steering / mass velocity = truncate (velocity + steering , max_speed) position = position + velocity When we add the governing forces, we get a vector representing all these forces. In the code snippet shown above, the resulting control force will force the character to search for something, while at the same time avoiding something else .
The following are examples of combined controlling forces creating a single controlling force:

Easy creation of complex patterns
. , , - , ?
, , , . , , .
steering behaviors . , , .
To use several steering behaviors simultaneously, it will be useful to create a motion manager . The idea is to write a “black box” that can be connected to any existing entity, which will allow it to carry out these behaviors.
The manager has a link to the entity to which it is connected (to the "host"). The manager passes a set of methods to the host, such as
seek()and flee(). With each call of such methods, the manager updates its internal properties to create a vector of controlling force.After processing all calls, the manager adds the resulting control force to the host speed vector. This changes the magnitude and direction of the host velocity vector in accordance with active behaviors.
The figure below shows the architecture:

Summarize the elements
, . .
, Seek , , ; Pursuit , .
Point Vector2D . .Pursuit , . , , , , «», " ? ". - .
,
IBoid , , steering behaviors, IBoid . : public interface IBoid { function getVelocity() :Vector3D; function getMaxVelocity() :Number; function getPosition() :Vector3D; function getMass() :Number; } , , . ( ), , :
public class SteeringManager { public var steering :Vector3D; public var host :IBoid; // public function SteeringManager(host :IBoid) { this.host = host; this.steering = new Vector3D(0, 0); } // API ( ) public function seek(target :Vector3D, slowingRadius :Number = 20) :void {} public function flee(target :Vector3D) :void {} public function wander() :void {} public function evade(target :IBoid) :void {} public function pursuit(target :IBoid) :void {} // . // public function update() :void {} // . public function reset() :void {} // API private function doSeek(target :Vector3D, slowingRadius :Number = 0) :Vector3D {} private function doFlee(target :Vector3D) :Vector3D {} private function doWander() :Vector3D {} private function doEvade(target :IBoid) :Vector3D {} private function doPursuit(target :IBoid) :Vector3D {} } When creating an instance of a manager, it should receive a link to the host to which it is connected. It will allow the manager to change the speed vector of the host in accordance with active behaviors.
Each behavior is represented by two methods - public and private. Take for example the behavior of Seek:
public function seek(target :Vector3D, slowingRadius :Number = 20) :void {} private function doSeek(target :Vector3D, slowingRadius :Number = 0) :Vector3D {} The public
seek()will be called to instruct the manager to apply this particular behavior. This method has no return value, and its parameters are associated with the behavior itself, for example, a point in space. Inside the private method will be called doSeek(), and its return value, i.e. the calculated control power of this particular behavior will be added to the steeringmanager property .The following code shows the implementation of seek:
// . // slowingRadius ( Arrival). public function seek(target :Vector3D, slowingRadius :Number = 20) :void { steering.incrementBy(doSeek(target, slowingRadius)); } // Seek ( Arrival) private function doSeek(target :Vector3D, slowingRadius :Number = 0) :Vector3D { var force :Vector3D; var distance :Number; desired = target.subtract(host.getPosition()); distance = desired.length; desired.normalize(); if (distance <= slowingRadius) { desired.scaleBy(host.getMaxVelocity() * distance/slowingRadius); } else { desired.scaleBy(host.getMaxVelocity()); } force = desired.subtract(host.getVelocity()); return force; } All other behaviors are implemented in a very similar way. For example, the method
pursuit()would look like this: public function pursuit(target :IBoid) :void { steering.incrementBy(doPursuit(target)); } private function doPursuit(target :IBoid) :Vector3D { distance = target.getPosition().subtract(host.getPosition()); var updatesNeeded :Number = distance.length / host.getMaxVelocity(); var tv :Vector3D = target.getVelocity().clone(); tv.scaleBy(updatesNeeded); targetFuturePosition = target.getPosition().clone().add(tv); return doSeek(targetFuturePosition); } We can use the code from the previous parts of the tutorial. The only thing that needs to be done is to adapt it in the form
behavior()and doBehavior()so that it can be added to the motion manager.Application and updating of the controlling forces
With each invocation of a behavior method, the resulting force calculated by it is added to the property of the
steeringmanager. Consequently, all control forces accumulate in this property.After calling all the behaviors, the manager must apply the current controlling force to the speed of the host so that it moves in accordance with the active behaviors. This is done in the
update()motion manager method : public function update():void { var velocity :Vector3D = host.getVelocity(); var position :Vector3D = host.getPosition(); truncate(steering, MAX_FORCE); steering.scaleBy(1 / host.getMass()); velocity.incrementBy(steering); truncate(velocity, host.getMaxVelocity()); position.incrementBy(velocity); } The method shown above should be called by the host (or any other game entity) after invoking all the behaviors. Otherwise, the host will never be able to change its velocity vector so that it matches active behaviors.
Application
Suppose we have a class
Preythat should move using steering behavior, but so far it has neither a control code nor a motion manager. Its structure will look like this: public class Prey { public var position :Vector3D; public var velocity :Vector3D; public var mass :Number; public function Prey(posX :Number, posY :Number, totalMass :Number) { position = new Vector3D(posX, posY); velocity = new Vector3D(-1, -2); mass = totalMass; x = position.x; y = position.y; } public function update():void { velocity.normalize(); velocity.scaleBy(MAX_VELOCITY); velocity.scaleBy(1 / mass); truncate(velocity, MAX_VELOCITY); position = position.add(velocity); x = position.x; y = position.y; } } With this structure, class instances can move using the Euler method . In order for us to use the manager, the class needs a property that refers to the motion manager, and it also has to use the interface
IBoid: public class Prey implements IBoid { public var position :Vector3D; public var velocity :Vector3D; public var mass :Number; public var steering :SteeringManager; public function Prey(posX :Number, posY :Number, totalMass :Number) { position = new Vector3D(posX, posY); velocity = new Vector3D(-1, -2); mass = totalMass; steering = new SteeringManager(this); x = position.x; y = position.y; } public function update():void { velocity.normalize(); velocity.scaleBy(MAX_VELOCITY); velocity.scaleBy(1 / mass); truncate(velocity, MAX_VELOCITY); position = position.add(velocity); x = position.x; y = position.y; } // , IBoid. public function getVelocity() :Vector3D { return velocity; } public function getMaxVelocity() :Number { return 3; } public function getPosition() :Vector3D { return position; } public function getMass() :Number { return mass; } } The method
update()needs to be changed accordingly so that the manager can also be updated: public function update():void { // , prey ... steering.wander(); // , prey. // , // "". steering.update(); // , // "". x = position.x; y = position.y; } ,
update() , .update() Prey, (seek) (evade) ( ): public function update():void { var destination :Vector3D = getDestination(); // , var hunter :IBoid = getHunter(); // , // (!) steering.seek(destination); steering.evade(hunter); // , prey. // , // "". steering.update(); // , // "". x = position.x; y = position.y; } Example
The example below shows a complex motion pattern that combines several behaviors. In the scene there are two types of characters: Hunter (hunter) and Prey (victim).
The hunter will pursue the victim if he gets close enough. He pursues her while he has energy (stamina). When the energy ends, the pursuit stops and the hunter begins to wander until he regains the energy level.
Here is
update()the Hunter class method : public function update():void { if (resting && stamina++ >= MAX_STAMINA) { resting = false; } if (prey != null && !resting) { steering.pursuit(prey); stamina -= 2; if (stamina <= 0) { prey = null; resting = true; } } else { steering.wander(); prey = getClosestPrey(position); } steering.update(); x = position.x; y = position.y; } . , . , .
update() Prey: public function update():void { var distance :Number = Vector3D.distance(position, Game.mouse); hunter = getHunterWithinRange(position); if (hunter != null) { steering.evade(hunter); } if (distance <= 300 && hunter == null) { steering.seek(Game.mouse, 30); } else if(hunter == null){ steering.wander(); } steering.update(); x = position.x; y = position.y; } Conclusion
steering behaviors. , .
, .
.
Source: https://habr.com/ru/post/358366/
All Articles