Symmetric cards as a means of minimizing Boolean functions

The memory of my father, Stanislav Plekhanov, is dedicated.

When it is necessary to synthesize a logic circuit and obtain a result with the minimum number of elements, in most cases Carnot maps are used. Carnot maps are studied in higher education institutions, engineering courses, etc. However, if your logical function has 5-6 inputs, using Carnot maps is quite problematic, and with more input variables, it is almost impossible at all. Surprisingly, there is a method that is much simpler and more efficient than Carnot maps, but which most developers do not know about.


')
The minimization method for Boolean functions, which is significantly more efficient than other existing methods, is based on the use of so-called “symmetric maps” [1, 2]. Why cards are called symmetrical, it will be clear from the further story. I will illustrate this method with an example.

Let given truth table with five input variables, shown in Fig. one.



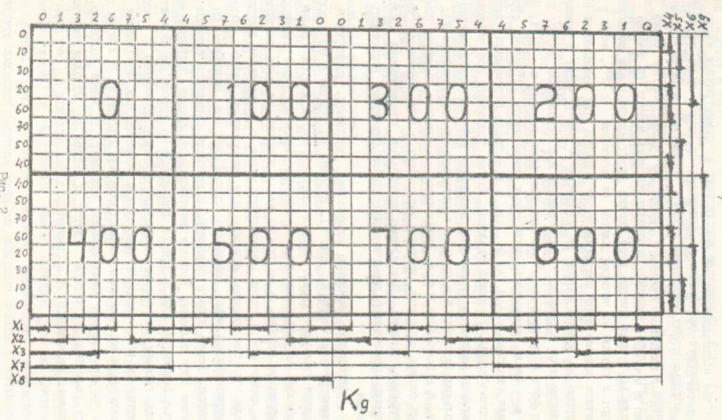
Let me remind you that the value “-” of the function F means an “indifferent” state, which says that such a set of input variables does not occur and the value of the function can be assigned by us arbitrarily zero or one in the process of minimization. The first thing to do is to number the input sets in the octal system (the last column in Figure 1). After this, the most symmetrical card is filled. A symmetrical map for five variables is shown in Figure 2.



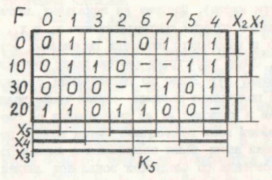
How to draw it will be shown later, but now I want to draw attention to the indexes of the columns that form the sequence 0, 1, 3, 2, 6, 7, 5, 4 and the sequence of lines ("tens" in the octal system) - 0, 10 30, 20.
Filling out such a table is much easier than carnot cards. To do this, take eight values ​​from the truth table and enter them into the appropriate row (column indices correspond to the number in the eight of the input set). After that, they proceed to the minimization of the Boolean function. Here the property of symmetry is used, which gives the name of this map.

Minimize the card by one. Take the unit in row 0 and the column with the index "1". We check all the cells “symmetrical” to this unit. First, in the "pair", that is, relative to the vertical axis, passing between the columns "0" and "1". This will be a cell in row 0 and index 0. There is a value of "0", so the "gluing" of these two values ​​cannot be done. We check the symmetry in the “four”, that is, relative to the vertical axis passing between columns 1 and 3. This is a cell in row 0 and index 3. There is the value “-”, which means that if we take it as “1”, we can combine (“ glue it ") with our unit. Next, check cell 5 of row 0, corresponding to the axis of symmetry between columns 2 and 6 (it can also be connected with our unit). The next symmetry in “sixteen” is a cell in row 10 and column 1 relative to the horizontal axis between rows 0 and 10. And finally, the symmetry in “thirty two” is a cell in row 20 and column 1 with a horizontal axis of symmetry between lines 10 and 30.
Our task is to find the largest possible figure, gluing our unit with others, symmetrical to it. There is the only such figure that covers the cells (row column): 0-1, 0-3, 0-7, 0-5, 10-1, 10-3, 10-7, 10-5. To get the implicant corresponding to this set, you just need to find the variables that describe this group either in direct or inverse form. Take the variable X1 (in Figure 2 it is marked with a vertical straight line to the right, with lines 0 and 10 being the thick line corresponding to the inverse value, and lines 30 and 20 being the thin line corresponding to the direct value). Our whole group of units falls into lines 0 and 10, therefore, X1 enters our implicant in inverse form. The variable X2, also shown on the right, will not enter our implicant, since the group falls into both the inverse (line 0) and the direct value of this variable (line 10). Similarly, the variables X3 and X4, shown by the horizontal lines at the bottom of the symmetric map, will not fall into our implicant, and the variable X5 will enter, since the whole group of units is described by the direct value of the variable X5. Finally, our unit group will be represented as (not X1) * X5.
Having dealt with the unit in row 0 and column 1, we look for the remaining units that are not included in the already formed groups. Take the unit in line 0 and index 4 (the last column). From it, you can get two equal-sized groups, the first of which contains cells in rows 0 and 10, the indices of columns 5 and 4, and the second - all the cells in the last column. Groups will correspond to implicants (not X1) * X3 * (not X4) and X3 * (not X4) * (not X5). Note that if there is more than one possibility of coverage, then there may also be more than one variants of the minimum Boolean function. We act in the same way until all units are covered by at least one group.

We finally have a minimal disjunctively normal form in the form of two options:



Symmetric maps for a different number of variables have a similar appearance, which is shown in the following figures.













Note that symmetric cards allow:

1. Significantly speed up and simplify the filling of the truth table.
2. Several times increase the number of arguments of the function to be minimized.
3. Significantly simplify the process of minimization due to the symmetry property.

1. Medvedev S.S. Octal maps for minimizing boolean functions. Automaton Theory. Sat articles, Institute of Cybernetics, USSR Academy of Sciences, 1966, p. 45-49.
2. Plekhanov S.P. Symmetric cards are a powerful tool for minimizing Boolean functions when designing digital devices of large dimensions. - Electronic equipment, Ser. 10, Microelectronic devices. - 1991. Vol. 4 (88), p. 27-29.