Theory of Computation. Introduction to state machines
Spoiler
I will tell you right away that I will not explain too formally.
Finite state machines
It is up to the limit of a simplified computer model with a finite number of states, which sacrifices all the features of computers such as RAM, read-only memory, I / O devices, and processor cores in exchange for ease of understanding, convenience of reasoning, and ease of software or hardware.
With the help of the spacecraft, you can implement such things as regular expressions, a lexical analyzer, AI in games, and so on.
Finite automata have a transition table , the current state of the automaton , the starting state and the final state .
')
Transition table - It stores transitions for the current state and the input symbol. The simplest implementation can be as a two-dimensional array.
Example 1
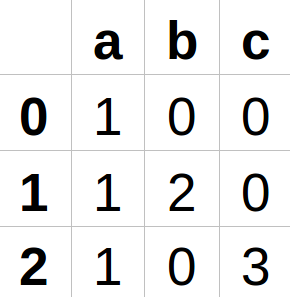
Here you can see that from state 0 to state 1 you can get only if we have the input symbol 'a', from state 1 to state 2, if the character 'b'.
- Horizontally at the top are possible input symbols.
- Vertically to the left are the current possible states.

Here you can see that from state 0 to state 1 you can get only if we have the input symbol 'a', from state 1 to state 2, if the character 'b'.
The current state is the set of states in which the automaton can be at a given time.
Starting state - the state where the spacecraft starts.
The final state - the set of states in which the automaton accepts a certain chain of symbols, otherwise rejects.
Deterministic finite automaton (deterministic finite automaton)
The simplest spacecraft, in which there can be one state at the current time, is deterministic.
Deterministic - for all states there is a maximum and minimum one rule for any possible input symbol, that is, for example, for state 1 there can be two transitions with the same input symbol.
Example 2
Here is a transition diagram for DFA, a visualization of Example 1. State 3 is inclusive. The diagram shows that DFA accepts a string of characters only if there is a sequence of characters 'a', 'b' and 'c'.

Here is a transition diagram for DFA, a visualization of Example 1. State 3 is inclusive. The diagram shows that DFA accepts a string of characters only if there is a sequence of characters 'a', 'b' and 'c'.
Nondeterministic finite automata (nondeterministic finite automaton)
The NCA is not a significant improvement in the DFA, it simply adds syntactic sugar, in the form of free transitions , non-determinism and state sets . You can implement as an array consisting of structures in which the state is stored, the input symbol and the next state.
Implementation of the NCA
// : _, _, _. struct state { unsigned char current; signed char sym; // signed, -1. unsigned char next; }; // 2 struct state machine[] = { {0, 'a', 1}, {1, 'a', 1}, {2, 'a', 1}, {1, 'b', 2}, {2, 'c', 3} }; Free transitions (epsilon transitions) - transitions that can be made without reading the input character.
Nondeterminism - zero or more transitions for a single character in any states.
Many states - at one time, the satellite can be in several states.
Example 3
The final state is indicated by a double circle.
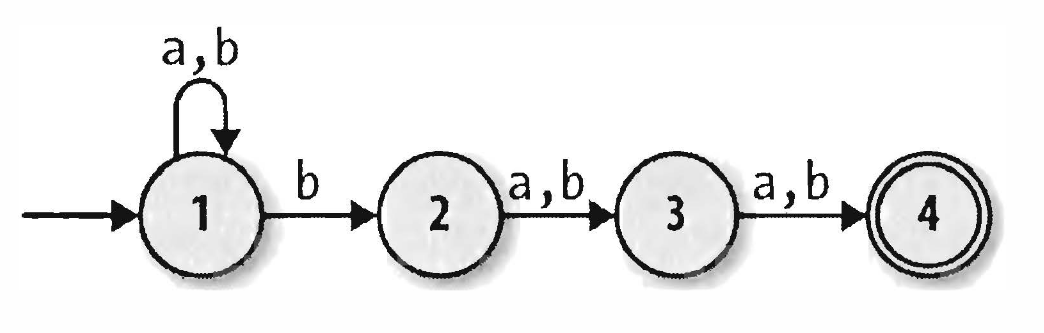
In the starting state, the current state is {1}, with the input symbol 'b' we have the opportunity to go to state 1 and state 2, that is, after the input character 'b', the current state is the set {1, 2}.

In the starting state, the current state is {1}, with the input symbol 'b' we have the opportunity to go to state 1 and state 2, that is, after the input character 'b', the current state is the set {1, 2}.
Example 4
Free transition is indicated by a dotted line.

Here you can see two free transitions from the starting state, that is, without reading the input symbol, we are immediately in the set state {2, 4}.

Here you can see two free transitions from the starting state, that is, without reading the input symbol, we are immediately in the set state {2, 4}.
To convert the NCA to the DFA, the Thompson algorithm is used.
When converting an NFA into a DFA, it may not turn out to be a very minimal DFA and to minimize it, you can apply the Brzhozovsky algorithm .
Pushdown automaton state machines
This is the same KA, but with additional memory in the form of a stack. Now, to make the transition, you need to take into account several other factors, the symbol that needs to be removed from the stack and the characters that need to be added to the stack .
CAMP can be used in places where there can be an unlimited number of investments, for example, when parsing languages, programming or counting nested brackets in mathematical expressions. It is impossible to implement with the help of a spacecraft, because the number of possible states is of course unlike the stack (I understand that memory is also finite).
Deleting a symbol from the stack - in any transition, it is decided which symbol to push out, if there was no such symbol on the top of the stack, then it is not pushed out. Also, if a character needs to be left on the stack, then it is added along with the added characters.
Adding characters to the stack - in any transition decides which characters to add to the stack.
Views :
- Deterministic - the same rules are applied to it as to the DFA; moreover, it completes the work only in the final state.
- Non - deterministic - the same rules apply to him as to NCAs; in addition, he can complete the work in the final state or when the stack is empty.
Example 5
Template: input_symbol; delete_character / character to add. The $ character is added to the bottom of the stack for what you understand when it is over.

This CAMP counts nesting of parentheses, by adding and removing characters from the stack.

This CAMP counts nesting of parentheses, by adding and removing characters from the stack.
DAMP is not equal to NAMP, therefore it is impossible to convert one into another, therefore NAMP has an advantage over DAMP.
Turing machine
The most powerful machine among the existing ones, its advantage over others in the tape with which it can work as it wants. There are no free transitions in it. Able to interpret other automata such as KA, CAMP.
A tape is a one-dimensional array in which data can be written at the expense of a head over a cell, which can be pre-filled with input data.
Example 6
Template: read_symbol_s_heads / recorded_symbol; side_surge_head. Ribbon edges are indicated by '_'.

This MT performs the increment of the binary number, the head stands on the left, where the tape starts.
Performance:

This MT performs the increment of the binary number, the head stands on the left, where the tape starts.
Performance:
- If it is in state 1 and zero is read, write one, move it to the right and go to state 2.
- If it is in state 1 and one is read, write zero, shift to the left and go to state 1.
- If it is in state 1 and an empty square is read, write down the unit, move it to the right and go to state 2.
- If it is in state 2 and read zero, write zero, move it to the right and stay in state 2.
- If it is in state 2 and unit is read, write unit, move it to the right and stay in state 2.
- If it is in state 2 and read the empty square, write down the empty square, move it to the left and go to state 3.
DMT is equivalent to NMT, so that they also do not differ.
Universal Turing machine (universal Turing machine)
A machine that can spawn other Turing machines, receiving machine data on the input tape.
Disadvantages :
- Memory generated machine can not be more than that of the UMT.
- It is necessary to be able to properly divide the tape space between the generated machine and the UMT, because their data are on the same tape.
On this introduction to the machines is completed, now you can continue to study further material yourself.
Literature:
Source: https://habr.com/ru/post/358304/
All Articles