Anti-interference coding. Part 1: Hamming code

Hamming code is not the purpose of this article. I just want to use his example to introduce you to the very principles of coding. But there will not be strict definitions, mathematical formulations, etc. This is just a good springboard for understanding more complex block codes.

Perhaps the most famous Hamming code (7,4). What do these numbers mean? The second, the number of bits of the information word, is what we want to convey safely and securely. And the first is the size of the code word: information fertilized with redundancy. By the way, the terms "information word" and "code word" are used in all 7 books on the theory of noise-resistant coding, which I happened to skim through.


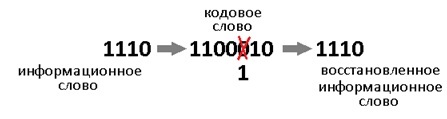
This code fixes one error. And no matter where it originated. Redundancy carries 3 bits of information, this is enough to indicate one of the 7 error positions or to show that it is not. That is exactly 8 answers we are waiting for. And 8 = 2 ^ 3, that's how it all matched.
')
To get a code word, you need to represent the information word in the form of a polynomial and multiply it by the generator polynomial g (x). Any number translated to binary can be represented as a polynomial. This may seem strange, and an unprepared reader immediately gets only one question: “why complicate things like that?”. I assure you, it will disappear by itself when we get the first results.

For example, the information word 1010, the value of each digit is the coefficient in a polynomial:


Many books write the opposite x + x ^ 3. Do not give in to provocation, this only causes confusion, because in the records of the number of 2-ary, hexadecimal, the low-order digits go to the right, and we make changes to the left / right by focusing on this. Now let's multiply this polynomial by the generator polynomial. The generator polynomial specifically for Hamming (7,4), meet: g (x) = x ^ 3 + x + 1. Where did he come from? Well, for now, consider that it is given to humanity from above, by the gods (I will explain later).


If you need to add coefficients, then we do modulo 2: the operation of addition is replaced by a logical exclusive or (XOR), that is, x ^ 4 + x ^ 4 = 0. And ultimately the result of multiplication, as you can see from 4 members. In binary form, this is 1001110. So, we received a code word that we will pass to the side through a noisy channel. Noting that by multiplying the information word (1010) by the generator polynomial (1011) as ordinary numbers, we get another result 1101110. We don’t need this, we need exactly “polynomial” multiplication. Software implementation of such multiplication is very simple. We will need 2 XOR operations and 2 left shifts (1st of which is by one bit, the second by two, in accordance with g (x) = 1011):


Let's now make a special mistake in the resulting code word. For example, in the 3rd category. Get the damaged word: 1000110.

How to decrypt the message and correct the error? Of course, it is necessary to “polynomially” divide the code word by g (x). Here I will not write X. Remember that modulo 2 subtraction is the same as addition, which, in turn, is the same as exclusive or. Go:


In the software implementation, again, nothing more complicated. The divider (1011) is shifted to the left by the end by 3 digits. And we begin to delete (not without the help of XOR) the left-most units in the dividend (100110), we don’t even look at its lower digits. The dividend gradually decreases 100110 -> 0011110 -> 0001000 -> 0000011, when there are no more units left in the 4th and left of the digits, we stop.

It did not work out completely, then we have a mistake (well, of course). The result of the division in this case, we needlessly. The remainder of the division is a syndrome, its size is equal to the size of redundancy, so we added zero there. In this case, the content of the syndrome does not help us to find the location of the damage. It's a pity. But if we take any other informational word, for example, 1100. In the same way, multiply it by g (x), we get 1110100, we introduce an error in the same category 1111100. Divide by g (x) and get the same syndrome in the remainder 011. And I guarantee you that we will come to this syndrome in common for all code words with an error in the 3rd digit. The conclusion suggests itself: you can create a table of syndromes for all 7 errors, making each of them specifically and considering the syndrome.


As a result, we collect a list of syndromes, and then what disease does it indicate:


Now we have everything. Found the syndrome, fixed the error, once again divided in this case 1001110 by 1011 and received in private our long-awaited information word 1010. In the remainder after the correction, there will already be 000. The table of syndromes has the right to life in the case of small codes. But for codes that fix a few bugs - there the list of syndromes is growing like a plague. Therefore, we consider the method of “catching errors” without having a table in hand.

The attentive reader will notice that the first 3 syndromes quite clearly indicate the position of the error. This applies only to those syndromes where one unit. The number of units in the syndrome call it "weight." Again, back to the ill-fated error in the 3rd digit. There, as you remember, there was 011 syndrome, its weight was 2, we were not lucky. Make a feint with your ears - cyclic shift of the code word to the right. The remainder of the division 0100011/1011 will be equal to 100, this is a "good syndrome", indicating that the error in the second digit. But since we made one shift, it means that the error has shifted by 1. That's actually the whole trick. Even in the case of terrible bad luck, when an error in the 6th discharge, you are sweating, after 3 agonizing divisions, but still find a mistake - this is a victory, only because you did not use the table of syndromes.

What about the other Hamming codes? I would say the Hamming codes are infinite: (7.4), (15.11), (31.26), ... (2 ^ m-1, 2 ^ m-1-m). The size of the redundancy is m. All of them correct one error, as the information word grows redundancy grows. Noise immunity weakens, but in case of weak noise the code is very economical. Well, well, how can I find the generating function for example (15,11)? Reasonable question. There is a theorem that says: the generator polynomial of the cyclic code g (x) divides (x ^ n + 1) without remainder. Where n is our case of a codeword size. In addition, the generator polynomial should be simple (divided only by 1 and on itself without a remainder), and its degree is equal to the size of the redundancy. It can be shown that for Hamming (7.4):


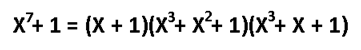
This code has as many as 2 generator polynomials. It would not be a mistake to use any of them. For the rest of the Hamming, use this table of primitive polynomials:


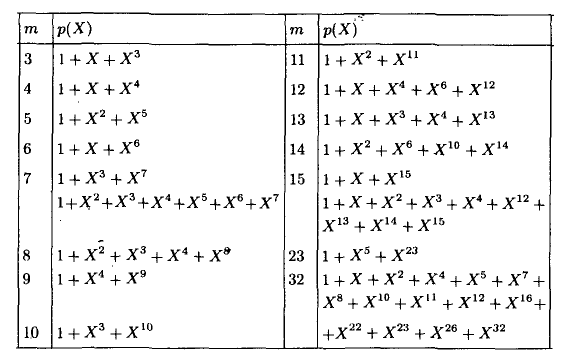
Accordingly, for (15.11) the generator polynomial g (x) = x ^ 4 + x + 1. Well, now turn to the dessert - to the matrix. It is usually started from this, but we will end it. To begin with, convert g (x) into a matrix by which you can multiply the information word by getting a code word. If g = 1011, then:


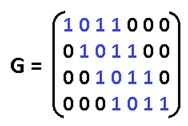
Call it a "generator matrix." We give the designation of the information word d = 1010, and the code is denoted by k, then:


This is a pretty elegant wording. The speed is even faster than the multiplication of polynomials. There it was necessary to make shifts, and here everything was already shifted. The vector d tells us which lines to take into account. The bottom row of the matrix is ​​zero, rows are numbered from bottom to top. Yes, yes, all because the low-order digits are located on the right and there is no getting away from it. Since d = 1010, then I take the 1st and 3rd rows, perform the XOR operation and voila over them. But that's not all, get ready to be surprised, there is still a test matrix H. Now, by multiplying the vector by the matrix, we can get the syndrome and no divisions of the polynomials are needed.


Look at the check matrix and the list of syndromes that you got above. This is the answer to the question where this matrix comes from. Here, as usual, I spoiled the code word in the 3rd digit, and I got the same syndrome. Since the matrix itself is the list of syndromes, we immediately find the position of the error. But in codes that fix a few errors, this method does not work. It is necessary to catch errors according to the method described above.

In order to better understand the very nature of error correction, let's generate in general all 16 codewords, because the information word consists of only 4 bits:


Look closely at the code words, they all differ from each other by at least 3 bits. For example, take the word 1011000, change any bit in it, say the first, to get 1011010. You will not find a similar word more than 1011000. As you can see, it’s not necessary to perform calculations to form a codeword, it’s enough to have this table in memory is small. The 3-bit difference shown is called the minimum “Hamming distance”, it is a characteristic of the block code, it is judged by how many errors can be corrected, namely (d-1) / 2. More generally, the Hamming code can be written as follows (7,4,3). I will only note that the Hamming distance is not the difference between the sizes of the code and information words. The Golay Code (23,12,7) fixes 3 errors. The code (48, 36, 5) was used in cellular communication with time division multiplexing (IS-54 standard). For Reed-Solomon codes, the same entry applies, but these are non-binary codes.

Bibliography:

1. M. Werner. Coding Basics (Programming World) - 2004
2. R. Morelos-Zaragoza. The art of noise immunity coding (World of Communications) - 2006
3. R. Blahut. Theory and practice of error control codes - 1986