Bubble expression evaluator: the simplest manual LR parser
Greetings dear community.
Recently, I paid some attention to the topic of syntactic analysis (with the goal of improving my own knowledge and skills), and I got the impression that almost all compiler courses start with mathematical formalisms and require a relatively high level of training from the student. Or there is used in a large number of formal mathematical writing, as in the classic Dragon Book, in which, for example, it says:
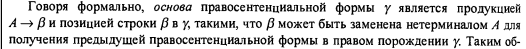
')
This can be a scary habit. No, from a certain moment a formal recording becomes convenient and even necessary, but for a “man from the street” who would like him to be “on his fingers” explained “what is the matter”, it can be difficult. And the question “what is LL and LR - analysis, and what is the difference between them” programmers are asked quite often (because not all programmers have a formal education in Computer Science, like me, and not all of them took a course on compilers ).
The approach is closer to me when we first take a task, try to solve it, and in the process of solving, we first develop an intuitive understanding of the principle, and then for this understanding we create mathematical formalisms. Therefore, I want to show by a very simple example in this article what kind of idea underlies the bottom-up parsing (aka bottom-up parsing, aka LR). We will calculate an arithmetic expression in which, for even greater simplification, we will support only the operators of addition, multiplication, and parentheses (so as not to complicate the example with negative numbers and support for a unary minus).
Before proceeding directly to the task, I will write some general considerations on the topic of syntactic analysis.
Syntax analysis is one of the fundamental concepts in computer science (in that part of it that of formal languages, actually programming languages), so almost any programmer comes to the need to understand this topic sooner or later. Especially when he begins to want to write some mini-interpreter of some mini-language, which sooner or later he wants to implement. Moreover, sometimes a programmer may not even realize that he constructs an interpreter, but think that he came up with a “convenient format” to describe some “rules” or “actions” or “configuration”, and now he needs “this format to read". In my opinion, this is a natural process that leads to the concept of language-oriented programming, when a general-purpose language is used to create the Domain Specific Language (DSL) interpreter, and then this DSL is increasingly used in the project, because it somehow it turns out that it is more convenient to describe this subject area using DSL.
Therefore, syntactic parsing and important that the interpreter can not be built without it. And the task of calculating arithmetic expressions is probably one of the simplest tasks, which already requires syntactic analysis to solve. Therefore, usually begin with this complex topic often begin with it.
How can I calculate an arithmetic expression? You can convert it to Reverse Polish Notation and calculate it on the stack, you can write an analyzer that calculates it by recursive descent, you can use the shunting yard algorithm, you can use the parser generator (ANTLR or bison), which, based on the compiled grammar, makes the parser, and calculate expression in it.
But using tools such as ANTLR or bison leaves you feeling that you started some kind of magic, you generated a grammar parser for the grammar you made, and then you use it and don’t understand how it works. As if you were given it from above by some higher powers that surpass the abilities of your understanding. In addition, when using these tools, we always start dancing from the grammar of the language that we want to make out, and the task in itself is not so simple to make up the grammar. You need to understand what it is, how it works, how to eliminate left-handed recursion (and what it is at all), why some grammars for LR may not work for LL and how to rewrite them, if necessary, to work, and all that. It can be difficult right away, especially if such a concept as “grammar” (and the preceding concepts “production”, “terminal symbol”, “non-terminal symbol”, “right-mental form” and many other scary words) is not yet included in the conceptual apparatus (“Active vocabulary”) of a programmer who is trying to write well, say, the same calculator of arithmetic expressions. Therefore, to understand the concept of upward parsing, you can try to solve some simple task, but independently.
We proceed to the problem: we will calculate the arithmetic expression using some kind of bottom-up analysis (if more precisely, this method is called “parsing the priority of operators”). The algorithm is not optimal, but easy to understand. It also reminds non-optimal, but understandable and, therefore, the well-known algorithm of bubble sorting.
In order not to go deep in particular, we will act as lazy sloths, and will only support the operators * (multiplication), + (addition) and parentheses. Before we go further, we will linger on the brackets.
In fact, imagine that we do not need to support brackets. Then the algorithm for calculating the expression is very simple and clear:
No parsing needed! The input structure is flat and no parsing is required to work with it. The need for it appears when there is a need to support parentheses (and other analogs are begin..end operator brackets, nested blocks, etc.). The input structure ceases to be flat and becomes tree-like (that is, self-similar, recursive), and from this point on, recursive methods and parsing methods must also be used to work with it. That is, for example, 5 * (2 + 3) is an expression, but (2 + 3) is also an expression. Both can be given as input to the expression parser. But about the syntactic analysis by the method of recursive descent we are not talking now, so let's go further.
In order not to do much of lexical analysis now, we’ll agree that the String.split function will act as a lexical analyzer (for those who have forgotten or are not in the subject yet, a lexical analyzer is such a thing that we give to the input it cuts it into an array of substrings (tokens). In our case, it will be, for example, '(2 + 3)' -> ['(', '2', '+', '3', ')'])
The informal description of our algorithm will be as follows:
How do we understand that we can perform the multiplication or addition operator? On the basis of the fact that to the left and to the right of the operator is a number. How do we understand that you can expand the brackets? When inside brackets there is only an expression in which there are no other brackets.
Actually, further, it seems to me, will be clear from the text of the program and the output of the result of its work. (Note that the program may have errors, it was written purely for demonstration purposes).
Work output:
Here it is. Real LR analyzers are much more complicated, they are usually not manually written, but they are used for automatic generation of formal grammars and special tools, such as bison (formerly it was yacc), which, based on grammars, generate software code that implements the LR analyzer. But the terminology shift-reduce, which is used in the description of such analyzers, I hope, has become clearer. When we scanned our string and added tokens to the stack, we did shift. When we used the operator of multiplication, addition, or open brackets - we did reduce.
Finally, I mention the LL-analysis (recursive descent). Historically, it appeared earlier than LR, a more or less general opinion is that it is relatively easy to write LL analyzers by hand, and LR are usually created using generators. But for the automatic generation of LL-analyzers there are also tools, one of the most famous - ANTLR. Probably, the ability to write LL-analyzer manually makes working with such tools easier. Which approach to apply (LL or LR) is a holivore question, so the answer is probably “who likes what, and who has what skills are better developed”.
Nevertheless, the LL analysis deserves a separate article, which I may write in the future (we will sort out something like JSON).
Recently, I paid some attention to the topic of syntactic analysis (with the goal of improving my own knowledge and skills), and I got the impression that almost all compiler courses start with mathematical formalisms and require a relatively high level of training from the student. Or there is used in a large number of formal mathematical writing, as in the classic Dragon Book, in which, for example, it says:
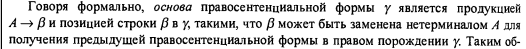
')
This can be a scary habit. No, from a certain moment a formal recording becomes convenient and even necessary, but for a “man from the street” who would like him to be “on his fingers” explained “what is the matter”, it can be difficult. And the question “what is LL and LR - analysis, and what is the difference between them” programmers are asked quite often (because not all programmers have a formal education in Computer Science, like me, and not all of them took a course on compilers ).
The approach is closer to me when we first take a task, try to solve it, and in the process of solving, we first develop an intuitive understanding of the principle, and then for this understanding we create mathematical formalisms. Therefore, I want to show by a very simple example in this article what kind of idea underlies the bottom-up parsing (aka bottom-up parsing, aka LR). We will calculate an arithmetic expression in which, for even greater simplification, we will support only the operators of addition, multiplication, and parentheses (so as not to complicate the example with negative numbers and support for a unary minus).
Before proceeding directly to the task, I will write some general considerations on the topic of syntactic analysis.
Syntax analysis is one of the fundamental concepts in computer science (in that part of it that of formal languages, actually programming languages), so almost any programmer comes to the need to understand this topic sooner or later. Especially when he begins to want to write some mini-interpreter of some mini-language, which sooner or later he wants to implement. Moreover, sometimes a programmer may not even realize that he constructs an interpreter, but think that he came up with a “convenient format” to describe some “rules” or “actions” or “configuration”, and now he needs “this format to read". In my opinion, this is a natural process that leads to the concept of language-oriented programming, when a general-purpose language is used to create the Domain Specific Language (DSL) interpreter, and then this DSL is increasingly used in the project, because it somehow it turns out that it is more convenient to describe this subject area using DSL.
Therefore, syntactic parsing and important that the interpreter can not be built without it. And the task of calculating arithmetic expressions is probably one of the simplest tasks, which already requires syntactic analysis to solve. Therefore, usually begin with this complex topic often begin with it.
How can I calculate an arithmetic expression? You can convert it to Reverse Polish Notation and calculate it on the stack, you can write an analyzer that calculates it by recursive descent, you can use the shunting yard algorithm, you can use the parser generator (ANTLR or bison), which, based on the compiled grammar, makes the parser, and calculate expression in it.
But using tools such as ANTLR or bison leaves you feeling that you started some kind of magic, you generated a grammar parser for the grammar you made, and then you use it and don’t understand how it works. As if you were given it from above by some higher powers that surpass the abilities of your understanding. In addition, when using these tools, we always start dancing from the grammar of the language that we want to make out, and the task in itself is not so simple to make up the grammar. You need to understand what it is, how it works, how to eliminate left-handed recursion (and what it is at all), why some grammars for LR may not work for LL and how to rewrite them, if necessary, to work, and all that. It can be difficult right away, especially if such a concept as “grammar” (and the preceding concepts “production”, “terminal symbol”, “non-terminal symbol”, “right-mental form” and many other scary words) is not yet included in the conceptual apparatus (“Active vocabulary”) of a programmer who is trying to write well, say, the same calculator of arithmetic expressions. Therefore, to understand the concept of upward parsing, you can try to solve some simple task, but independently.
We proceed to the problem: we will calculate the arithmetic expression using some kind of bottom-up analysis (if more precisely, this method is called “parsing the priority of operators”). The algorithm is not optimal, but easy to understand. It also reminds non-optimal, but understandable and, therefore, the well-known algorithm of bubble sorting.
In order not to go deep in particular, we will act as lazy sloths, and will only support the operators * (multiplication), + (addition) and parentheses. Before we go further, we will linger on the brackets.
In fact, imagine that we do not need to support brackets. Then the algorithm for calculating the expression is very simple and clear:
- Scan the line from left to right, and execute all multiplication operators (for example, the input line was 1 + 5 * 7 + 3, the output is 1 + 35 + 3)
- Scan what happened in step 1 and execute all the addition operators (it was at the input 1 + 35 + 3, it turned out at the output 39).
- Give what happened in step 2, as a result.
No parsing needed! The input structure is flat and no parsing is required to work with it. The need for it appears when there is a need to support parentheses (and other analogs are begin..end operator brackets, nested blocks, etc.). The input structure ceases to be flat and becomes tree-like (that is, self-similar, recursive), and from this point on, recursive methods and parsing methods must also be used to work with it. That is, for example, 5 * (2 + 3) is an expression, but (2 + 3) is also an expression. Both can be given as input to the expression parser. But about the syntactic analysis by the method of recursive descent we are not talking now, so let's go further.
In order not to do much of lexical analysis now, we’ll agree that the String.split function will act as a lexical analyzer (for those who have forgotten or are not in the subject yet, a lexical analyzer is such a thing that we give to the input it cuts it into an array of substrings (tokens). In our case, it will be, for example, '(2 + 3)' -> ['(', '2', '+', '3', ')'])
The informal description of our algorithm will be as follows:
- Scan the string, open all the brackets we can.
- Scan the string, execute all multiplication operators as we can.
- Scan the string, execute all the addition operators as we can.
How do we understand that we can perform the multiplication or addition operator? On the basis of the fact that to the left and to the right of the operator is a number. How do we understand that you can expand the brackets? When inside brackets there is only an expression in which there are no other brackets.
Actually, further, it seems to me, will be clear from the text of the program and the output of the result of its work. (Note that the program may have errors, it was written purely for demonstration purposes).
package demoexprevaluator; import java.io.PrintStream; import java.util.ArrayList; public class DemoExprEvaluator { // Java... public class CalcResult { public boolean operationOccured; public String resultString; public CalcResult(boolean op, String r){ this.operationOccured = op; this.resultString = r; } } // public String spreadSpaceBetweenTokens(String s){ StringBuilder r = new StringBuilder(); for (int i = 0; i<s.length(); i++){ Character c = s.charAt(i); if (c.equals('(') || c.equals(')') || c.equals('+') || c.equals('*')) { r.append(" ").append(c).append(" "); } else if (Character.isDigit(c)) { r.append(c); } } return r.toString().trim(); } // String.split public String[] getLexems(String expr) { expr = spreadSpaceBetweenTokens(expr); String[] lexems = expr.split("\\s+"); // , () return lexems; } // . public String applyOperator(String exprWithoutParens, String operator) { ArrayList<String> stack = new ArrayList<>(); String[] lexems = getLexems(exprWithoutParens); for(int i = 0; i < lexems.length; i++) { stack.add(lexems[i]); if (stack.size() >= 3) { String left = stack.get(stack.size()-3); String middle = stack.get(stack.size()-2); String right = stack.get(stack.size()-1); if (Character.isDigit(left.charAt(0)) && middle.equals(operator) && Character.isDigit(right.charAt(0))){ Integer operand1 = Integer.valueOf(left); Integer operand2 = Integer.valueOf(right); Integer res = 0; if (operator.equals("*")) { res = operand1 * operand2; } if (operator.equals("+")) { res = operand1 + operand2; } stack.remove(stack.size()-1); // like "pop" stack.remove(stack.size()-1); stack.remove(stack.size()-1); stack.add(res.toString()); } } } return String.join("", stack); } // , public String evalExprWithoutParens(String exprWithoutParens) { // : , String result = applyOperator(exprWithoutParens, "*"); result = applyOperator(result, "+"); return result; } // , // , // , // , , // ...(2+2)... -> ...4... public CalcResult openSingleParen(String expr) { CalcResult r = new CalcResult(false, expr); String[] lexems = getLexems(expr); ArrayList<String> stack = new ArrayList<>(); int lpindex = 0; for(int i = 0; i < lexems.length; i++){ String lexem = lexems[i]; stack.add(lexem); if (lexem.equals("(")) { lpindex = i; } if (lexem.equals(")") && !r.operationOccured) { stack.remove(stack.size()-1); int numOfItemsToPop = i - lpindex - 1; StringBuilder ewp = new StringBuilder(); // ewp <=> expression without parethesis for (int j = 0; j < numOfItemsToPop; j++) { ewp.insert(0, stack.get(stack.size()-1)); stack.remove(stack.size()-1); } System.out.println("about to eval ewp:" + ewp); String ewpEvalResult = evalExprWithoutParens(ewp.toString()); stack.remove(stack.size()-1); // removing opening paren from stack stack.add(ewpEvalResult); r.operationOccured = true; } } r.resultString = String.join("", stack); return r; } public void Calculate(String expr) { System.out.println("They want us to calculate:" + expr); CalcResult r = new CalcResult(false, expr); // while (true) { System.out.println(r.resultString); r = openSingleParen(r.resultString); if (!r.operationOccured) { break; } } // r.resultString , r.resultString = evalExprWithoutParens(r.resultString); System.out.println("The result is: " + r.resultString); } public static void main(String[] args) { DemoExprEvaluator e = new DemoExprEvaluator(); String expr = "2+300*(4+2)*((8+5))"; e.Calculate(expr); } } Work output:
They want us to calculate:2+300*(4+2)*((8+5))
2+300*(4+2)*((8+5))
about to eval ewp:4+2
2+300*6*((8+5))
about to eval ewp:8+5
2+300*6*(13)
about to eval ewp:13
2+300*6*13
The result is: 23402Here it is. Real LR analyzers are much more complicated, they are usually not manually written, but they are used for automatic generation of formal grammars and special tools, such as bison (formerly it was yacc), which, based on grammars, generate software code that implements the LR analyzer. But the terminology shift-reduce, which is used in the description of such analyzers, I hope, has become clearer. When we scanned our string and added tokens to the stack, we did shift. When we used the operator of multiplication, addition, or open brackets - we did reduce.
Finally, I mention the LL-analysis (recursive descent). Historically, it appeared earlier than LR, a more or less general opinion is that it is relatively easy to write LL analyzers by hand, and LR are usually created using generators. But for the automatic generation of LL-analyzers there are also tools, one of the most famous - ANTLR. Probably, the ability to write LL-analyzer manually makes working with such tools easier. Which approach to apply (LL or LR) is a holivore question, so the answer is probably “who likes what, and who has what skills are better developed”.
Nevertheless, the LL analysis deserves a separate article, which I may write in the future (we will sort out something like JSON).
Source: https://habr.com/ru/post/357052/
All Articles