Passive Censorship Bandwidth
One of the problems of the modern Internet is the surveillance and unauthorized access to user data. The downside of this phenomenon, which is recalled somewhat less often, is unauthorized restriction of access to data. Or, simply, censorship.
About her and invited to talk today. Quantify how it works depending on the complexity of the incoming information, and understand what and how much it goes through it.
')
So, suppose, the flow of information to you blocks a certain filter. Trying to cut off everything that he does not like. The filter is passive - that is, it itself does not amplify any signals, but only suppresses undesirable ones.
Life examples are numerous and show that censorship, in fact, is not always evil:
The effectiveness of censorship depends on the complexity of the information submitted. Messages are simple to detect and cut off easily. Non-trivial messages are more likely to slip through the filter.
For example, let's say someone decided to ban the propaganda of the Pythagorean Theorem online. You can imagine the following levels of complexity of this propaganda:
1. “Pythagoras is a genius, and you are all %%% you!” - low complexity. Contains nothing but confidence and emotion. To understand this argument is enough ability to read. Immediately, we note: we are not talking about agreement with the argument or its loyalty. We are only talking about understanding.
Recognizing and blocking such an argument is quite simple.
2. "Formulas connecting the lengths of the sides of rectangular triangles, used in the construction of bridges, buildings, manufacturing machines, in cartography and laying routes of aircraft." This is more difficult. The appeal goes to the branches of modern industry and to geometry. It is required at least to know about their availability. This is the 7th grade school. The premise of the conclusion is hidden: "... and since all these industries work, the Pythagorean Theorem is also" - and requires a certain concentration of mind from the censor. Especially considering that the theorem itself is also not explicitly mentioned.
3. A drawing of a rare proof of the theorem is given (for example, [ 10 ]), preferably in a decorative form. From the reader is required meditative peering into the drawing and the possession of geometry, in order to come to the right conclusion most suddenly. And although at school this theorem is passed, in practice rarely anyone besides entering a technical college of higher education is ready to voluntarily repeat its proof.
4. You can imagine something else. Say, how can the string "huxj5lh" be related to the Pythagorean theorem?
So here. It turns out that throughput of passive censorship one can make several mathematically precise quantitative conclusions that are true with very broad assumptions. We list them:
First and foremost, the censor and receiver are entities of the same class. For example, people and people. That is, the filter can be represented as a set of the same receivers, only oriented not to the perception, but to the suppression of information.
Second: the receiver and the filter equally monotonously perceive the complexity of the incoming information. That is, if A is more complicated than B, for you, then in the same order is the complexity for censorship.
Third: censorship is much more powerful, “thicker” than the receiver.
Under these assumptions, it can be argued that the maximum of your ability to capture leaked information through “thick” passive censorship is at such a level of complexity, where the throughput of censorship is 37%
Who cares - proof below. Who is not, go to the section with conclusions and examples.
It is clear that the effectiveness of perception behind a layer of censorship depends on the complexity of the messages. Too simple information is easily filtered and does not reach the recipient. Too complex is not recognized and passes through - but, unfortunately, it is too difficult for the listener to understand and notice. This means that the peak of the ability to capture information that was mistakenly missed by the censor should be somewhere in the area of "intermediate" complexity. Question: where exactly?
Let x denote the complexity of the incoming packet of information. S (x) - “sensitivity” of censorship to packages of a certain complexity, expressed as the probability of detecting and cutting this information. This sensitivity is strictly decreasing, it looks like this:

Then the “transmissive” ability of censorship is obviously 1-S (x):

All that passed, comes to you. Your sensitivity is Q (x) - probably with a threshold lower than that of censorship. Qualitatively somehow:

The signal that you still hear is the product of what has passed, what you can hear, i.e. Q (x) * (1-S (x)):
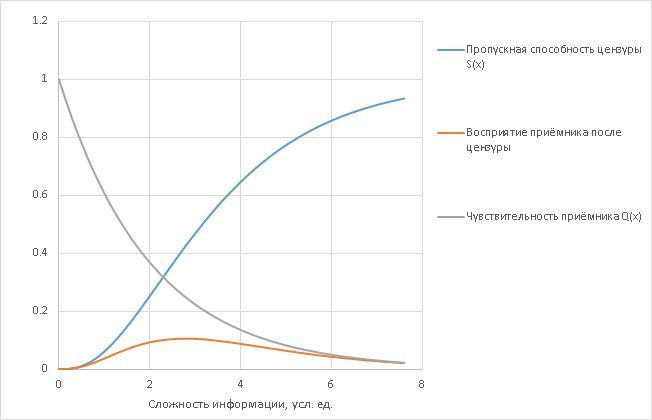
Until this place, everything is abstract. Now let us recall the main assumption: that censorship is carried out by elements of the same type as receivers. Therefore, it can be mentally imagined as a set of N >> 1 filter elements operating more or less independently (if they are dependent, you just need to represent each synchronized group as a separate detector, changing the effective value of N).
Let the sensitivity of each element of censorship be s (x) - that is, with such a probability its employee detects that “wrong” information is trying to slip through it. Accordingly, with probability 1-s (x), he does not notice this, missing a packet. If there are N elements, then the probability that they all miss the packet is (1-s (x)) N.
Since you are also a person with abilities similar to those of censorship workers, your sensitivity is approximately equal to that of her employee, i.e. Q (x) ≈ s (x).
Multiplying, we get the amount of flow of information that you still perceive:
I (x) ≈ s (x) * (1-s (x)) N
Let's find its maximum. To do this, differentiate this expression with respect to x and force it to be equal to zero:
0 = ∂I (x) / ∂x = (∂I (s) / ∂s) * (∂s / ∂x) = (∂s / ∂x) * [(1-s (x)) N - N * s * (1-s (x)) N-1 ] = 0.
Since s (x) is monotone (assumption 2), its derivative can be reduced. As well as the value (1-s (x)) N-1 . It remains:
(1-s) - sN = 0, or
s * = 1 / (N + 1)
That is, the maximum perception of information will be at the level of its complexity, where your perceptive ability is 1 / (N + 1). What is the filtering ability of censorship at this level? Substituting s * into (1- s (x)) N , we get:
S * = S (x | s (x) = s *) = (1-1 / (N + 1)) N
As N grows, this expression very quickly tends to ... the golden limit, which is simply 1 / e, or 37%! With decent accuracy, this happens already with N of the order of 3-4:
So, the maximum of your perception behind a powerful layer of passive censorship is where its bandwidth is 37% . And since the answer is very weakly dependent on the “thickness” of N censorship, it remains true with rather far deviations from the model. Any filter that can be at least approximately represented as a set of independent receivers with a sufficiently large number N will satisfy this conclusion.
It is only important that the complexity of the information remains “one-dimensional” and monotonous. Without messages that are trivial for you, but very difficult for censorship and it passes them through (or vice versa).
So, the maximum perceptible ability “behind censorship” falls on that level of signal complexity, at which it misses 37% of the facts.
What is the benefit of this knowledge?
Well, first of all, if you managed to catch one packet that broke through the filtering, it is useful and pleasant to know: in fact, 2-3 of these packets were sent. And even N + 1 times more packages of primitive, but completely suppressed. The world is balanced substantially differently than seen through filtering.
And secondly, it can be used to detect it. The way is expensive and slow, but better than nothing. It works like this.
Let us assume that there are two points of view, A and B, on a certain question. A - “resolved”, censored to be 100% passed regardless of the level of complexity. And B, forbidden, filtered. At the entrance you have a large set of statements {F}, speaking for both A and B. You can understand by their relationship, is something filtered, and if so, what exactly?
Sort statements F by complexity for perception x. Of course, subjectively, there are no other options. How we can. But trying carefully. Simple to the left, complex to the right, the rest somewhere between them approximately in ascending order. It turned out the sequence F (x). And now we look, how the share of points of view A and B is distributed depending on the complexity.
A is not censored, i.e. comes to us through and through at any level of complexity that we still perceive. Assuming that the censorship is not more than one, the number of messages A (x) will be constant.
Radically different, B (x) will behave. In the field of the simplest messages, there will be almost no options for B (they were all filtered out!) Then their number will start growing until it reaches a constant characterizing the "unfiltered" ratio of opinions.
If we draw the proportions A / (A + B) and B / (A + B) as functions of x, then, if there is censorship, something like this is expected:
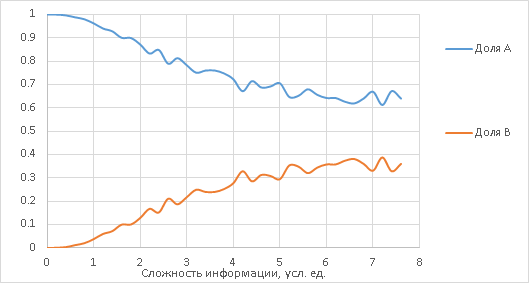
When the graphs are approximately the same, then with some reason we can assume that a) passive censorship is in effect, and: b) it is precisely variant B that is suppressed.
And if the schedule looks like this?

Then, most likely, there is no censorship. Or we are not smart enough to notice. Well, or it is not passive, which requires completely different methods.
It is important to repeat that in this case no one says that option B is true. The official version of A. may well be the truth. To distinguish truth from falsehood is a task of much greater complexity. Our goal is simpler: to understand in which direction the image is “tilted” to us. But only.
Let's try to apply what we have counted here in practice.
Test 1 (the simplest): photography . Here I have a sheet of silicon (Si) 0.7 mm thick in my hand:

What happens if you use it as a filter for a digital camera with a remote IR filter? The receiver is actually silicon, 15 microns. And the filter is silicon. The same material, only thicker, 700 microns. The “complexity” is the wavelength of light. The theory predicts that the maximum sensitivity of such a system will fall on the wavelength at which the input filter transmits 37% of the radiation. We look at the graph of the transparency of silicon from the wavelength (s [ 20 ]).

I drew on it the red line corresponding to the inverse thickness of 1 / 0.07 cm. Where it intersects the transmission curve of silicon, the transparency of the filter is e -1 = 37%. This occurs at a wavelength of 1050 nm. This means that there should also be a maximum sensitivity of the camera with such a filter. I do not have a spectrograph, but this can be indirectly approximately verified by another method. Photographing through a silicon water bottle:

The water is dark. Why? Because at 1050 microns its effective transmission drops to ~ 5 centimeters ([ 30 ]). For comparison, at 800 nm and, of course, in visible light, this is not at all the case:


It means that the peak of perception of such a camera is really somewhere in the region of 1000-1100 microns. As expected.
The second example is more interesting. This seems to be a neutral video about the distribution of professions between Republicans and Democrats in the United States: www.youtube.com/watch?v=R34rXt_q2sY . Of course, he has a lot of comments both for and against each of the parties. Comments on complexity can be divided into three levels:
What does theory expect? The Republican and Democratic parties are about equal in strength. Even if they wish, they are unlikely to seriously crush the opposing side on the widely visible public spot. Accordingly, the arguments “for” and “against” each party should be presented approximately evenly throughout the whole range of complexity perceived by me. Take Excel, spend three hours reading comments, and - the result:
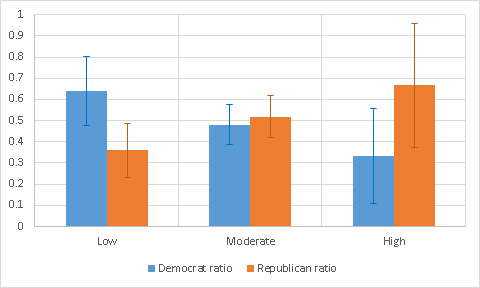
There is a slight bias in the direction of more “stupid” arguments from the Democrats, but in general, the difference lies within the limits of statistical noise. No serious indications of the presence of censorship have been found, at least within the range of complexity available to my personal intelligence.
Take the more interesting example number 3 : “Did the Americans fly to the moon?” YouTube is our everything, here’s a video stating that lunar landings are a complete deception: www.youtube.com/watch?v=vPRyo4cSESQ . Sort comments by complexity again (I had enough pieces for 80):
Result. (Pro - that the Americans were still on the moon, Con - what did not):
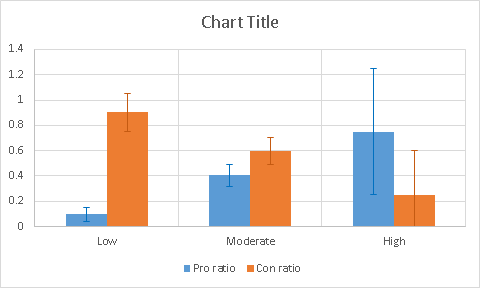
Och-chen interesting! Arguments “you,% spruce!” Dominate among those who believe lunar expeditions by deception. With increasing complexity (“but what about cosmic radiation?”), Their proportion noticeably decreases. Unfortunately, comments of high complexity are too few, such is the youtube audience. But even at two points there is a weighty impression that statements for the reality of flights to the moon in this video are censored. Does the author himself do this? Permissible. But much more likely is another explanation: people who do not take Moon hoax seriously simply don’t use rude and unreasonable “arguments”. A kind of internal, subculturally conditioned censorship. And, by the way, in vain. Reasoning about laser rangefinders to their opponents to the bulb because of incomprehensibility. But the simple "in our school only %%%% s still believe in Moon Hoax" may be more effective :))
So passive censorship is, in principle, detectable. Maximum ability to hear something through it falls on the level of complexity of messages, where its bandwidth is 37%. Quantifying the transmission curves as a function of the complexity of the incoming information, one can draw practical conclusions about the presence and strength of censorship.
Of course, the described method has a lot of disadvantages. He is subjectively dependent, he can give erroneous results with deviations from the model. Finally, it is important to remember that it is not at all quick and not cheap. Even on the measurement of the transmission curve at two points with a modest accuracy of 20% with 1σ confidence, about 50 messages are required, with the most optimistic scenario. Each of which must be read, understood, correlated with the party in the discussion and, most importantly, to assess the level of complexity. By doing this, it is necessary to manually, if you are interested in censorship is human, not automatic. This is a couple of hours of time.
So the method requires labor and patience. But if someone still seems useful or interesting - well, it means that time is spent not in vain.
Thank,
Eugene
About her and invited to talk today. Quantify how it works depending on the complexity of the incoming information, and understand what and how much it goes through it.
')
Intuitive description of the task
So, suppose, the flow of information to you blocks a certain filter. Trying to cut off everything that he does not like. The filter is passive - that is, it itself does not amplify any signals, but only suppresses undesirable ones.
Life examples are numerous and show that censorship, in fact, is not always evil:
- Antivirus. One input system partially emulates the behavior of potentially executable code in an attempt to recognize its possible harmfulness. Another, similar, system executes this code - and can fall victim to an attack if the antivirus is mistaken and there is no other protection.
- Blocking sites. One group of people reads the contents of the Internet and decides which sites to block. People from another group also read the Internet, including forbidden sites. If the contents of the latter are sufficiently allegorical, then their thought can be understood by the addressee, although it is omitted by censorship.
- Wikipedia (and any public forum). Here the censor is the readers themselves; thoughts or articles that are incorrect are simply edited.
- Messages from the authorities in any fairly large office with the number of “layers” L >> 1.
- And even the light filter on the camera. Cutting off some wavelengths, it allows others to reach the camera matrix and form a useful image for us.
The effectiveness of censorship depends on the complexity of the information submitted. Messages are simple to detect and cut off easily. Non-trivial messages are more likely to slip through the filter.
For example, let's say someone decided to ban the propaganda of the Pythagorean Theorem online. You can imagine the following levels of complexity of this propaganda:
1. “Pythagoras is a genius, and you are all %%% you!” - low complexity. Contains nothing but confidence and emotion. To understand this argument is enough ability to read. Immediately, we note: we are not talking about agreement with the argument or its loyalty. We are only talking about understanding.
Recognizing and blocking such an argument is quite simple.
2. "Formulas connecting the lengths of the sides of rectangular triangles, used in the construction of bridges, buildings, manufacturing machines, in cartography and laying routes of aircraft." This is more difficult. The appeal goes to the branches of modern industry and to geometry. It is required at least to know about their availability. This is the 7th grade school. The premise of the conclusion is hidden: "... and since all these industries work, the Pythagorean Theorem is also" - and requires a certain concentration of mind from the censor. Especially considering that the theorem itself is also not explicitly mentioned.
3. A drawing of a rare proof of the theorem is given (for example, [ 10 ]), preferably in a decorative form. From the reader is required meditative peering into the drawing and the possession of geometry, in order to come to the right conclusion most suddenly. And although at school this theorem is passed, in practice rarely anyone besides entering a technical college of higher education is ready to voluntarily repeat its proof.
4. You can imagine something else. Say, how can the string "huxj5lh" be related to the Pythagorean theorem?
So here. It turns out that throughput of passive censorship one can make several mathematically precise quantitative conclusions that are true with very broad assumptions. We list them:
First and foremost, the censor and receiver are entities of the same class. For example, people and people. That is, the filter can be represented as a set of the same receivers, only oriented not to the perception, but to the suppression of information.
Second: the receiver and the filter equally monotonously perceive the complexity of the incoming information. That is, if A is more complicated than B, for you, then in the same order is the complexity for censorship.
Third: censorship is much more powerful, “thicker” than the receiver.
Under these assumptions, it can be argued that the maximum of your ability to capture leaked information through “thick” passive censorship is at such a level of complexity, where the throughput of censorship is 37%
Who cares - proof below. Who is not, go to the section with conclusions and examples.
Mathematical Description
It is clear that the effectiveness of perception behind a layer of censorship depends on the complexity of the messages. Too simple information is easily filtered and does not reach the recipient. Too complex is not recognized and passes through - but, unfortunately, it is too difficult for the listener to understand and notice. This means that the peak of the ability to capture information that was mistakenly missed by the censor should be somewhere in the area of "intermediate" complexity. Question: where exactly?
Let x denote the complexity of the incoming packet of information. S (x) - “sensitivity” of censorship to packages of a certain complexity, expressed as the probability of detecting and cutting this information. This sensitivity is strictly decreasing, it looks like this:

Then the “transmissive” ability of censorship is obviously 1-S (x):

All that passed, comes to you. Your sensitivity is Q (x) - probably with a threshold lower than that of censorship. Qualitatively somehow:

The signal that you still hear is the product of what has passed, what you can hear, i.e. Q (x) * (1-S (x)):

Until this place, everything is abstract. Now let us recall the main assumption: that censorship is carried out by elements of the same type as receivers. Therefore, it can be mentally imagined as a set of N >> 1 filter elements operating more or less independently (if they are dependent, you just need to represent each synchronized group as a separate detector, changing the effective value of N).
Let the sensitivity of each element of censorship be s (x) - that is, with such a probability its employee detects that “wrong” information is trying to slip through it. Accordingly, with probability 1-s (x), he does not notice this, missing a packet. If there are N elements, then the probability that they all miss the packet is (1-s (x)) N.
Since you are also a person with abilities similar to those of censorship workers, your sensitivity is approximately equal to that of her employee, i.e. Q (x) ≈ s (x).
Multiplying, we get the amount of flow of information that you still perceive:
I (x) ≈ s (x) * (1-s (x)) N
Let's find its maximum. To do this, differentiate this expression with respect to x and force it to be equal to zero:
0 = ∂I (x) / ∂x = (∂I (s) / ∂s) * (∂s / ∂x) = (∂s / ∂x) * [(1-s (x)) N - N * s * (1-s (x)) N-1 ] = 0.
Since s (x) is monotone (assumption 2), its derivative can be reduced. As well as the value (1-s (x)) N-1 . It remains:
(1-s) - sN = 0, or
s * = 1 / (N + 1)
That is, the maximum perception of information will be at the level of its complexity, where your perceptive ability is 1 / (N + 1). What is the filtering ability of censorship at this level? Substituting s * into (1- s (x)) N , we get:
S * = S (x | s (x) = s *) = (1-1 / (N + 1)) N
As N grows, this expression very quickly tends to ... the golden limit, which is simply 1 / e, or 37%! With decent accuracy, this happens already with N of the order of 3-4:
| N | S * |
| one | 0.50 |
| 2 | 0.44 |
| 3 | 0.42 |
| four | 0.41 |
| five | 0.40 |
| ten | 0.38 |
So, the maximum of your perception behind a powerful layer of passive censorship is where its bandwidth is 37% . And since the answer is very weakly dependent on the “thickness” of N censorship, it remains true with rather far deviations from the model. Any filter that can be at least approximately represented as a set of independent receivers with a sufficiently large number N will satisfy this conclusion.
It is only important that the complexity of the information remains “one-dimensional” and monotonous. Without messages that are trivial for you, but very difficult for censorship and it passes them through (or vice versa).
Practical use
So, the maximum perceptible ability “behind censorship” falls on that level of signal complexity, at which it misses 37% of the facts.
What is the benefit of this knowledge?
Well, first of all, if you managed to catch one packet that broke through the filtering, it is useful and pleasant to know: in fact, 2-3 of these packets were sent. And even N + 1 times more packages of primitive, but completely suppressed. The world is balanced substantially differently than seen through filtering.
And secondly, it can be used to detect it. The way is expensive and slow, but better than nothing. It works like this.
Let us assume that there are two points of view, A and B, on a certain question. A - “resolved”, censored to be 100% passed regardless of the level of complexity. And B, forbidden, filtered. At the entrance you have a large set of statements {F}, speaking for both A and B. You can understand by their relationship, is something filtered, and if so, what exactly?
Sort statements F by complexity for perception x. Of course, subjectively, there are no other options. How we can. But trying carefully. Simple to the left, complex to the right, the rest somewhere between them approximately in ascending order. It turned out the sequence F (x). And now we look, how the share of points of view A and B is distributed depending on the complexity.
A is not censored, i.e. comes to us through and through at any level of complexity that we still perceive. Assuming that the censorship is not more than one, the number of messages A (x) will be constant.
Radically different, B (x) will behave. In the field of the simplest messages, there will be almost no options for B (they were all filtered out!) Then their number will start growing until it reaches a constant characterizing the "unfiltered" ratio of opinions.
If we draw the proportions A / (A + B) and B / (A + B) as functions of x, then, if there is censorship, something like this is expected:

When the graphs are approximately the same, then with some reason we can assume that a) passive censorship is in effect, and: b) it is precisely variant B that is suppressed.
And if the schedule looks like this?

Then, most likely, there is no censorship. Or we are not smart enough to notice. Well, or it is not passive, which requires completely different methods.
It is important to repeat that in this case no one says that option B is true. The official version of A. may well be the truth. To distinguish truth from falsehood is a task of much greater complexity. Our goal is simpler: to understand in which direction the image is “tilted” to us. But only.
Testing method
Let's try to apply what we have counted here in practice.
Test 1 (the simplest): photography . Here I have a sheet of silicon (Si) 0.7 mm thick in my hand:
What happens if you use it as a filter for a digital camera with a remote IR filter? The receiver is actually silicon, 15 microns. And the filter is silicon. The same material, only thicker, 700 microns. The “complexity” is the wavelength of light. The theory predicts that the maximum sensitivity of such a system will fall on the wavelength at which the input filter transmits 37% of the radiation. We look at the graph of the transparency of silicon from the wavelength (s [ 20 ]).

I drew on it the red line corresponding to the inverse thickness of 1 / 0.07 cm. Where it intersects the transmission curve of silicon, the transparency of the filter is e -1 = 37%. This occurs at a wavelength of 1050 nm. This means that there should also be a maximum sensitivity of the camera with such a filter. I do not have a spectrograph, but this can be indirectly approximately verified by another method. Photographing through a silicon water bottle:

The water is dark. Why? Because at 1050 microns its effective transmission drops to ~ 5 centimeters ([ 30 ]). For comparison, at 800 nm and, of course, in visible light, this is not at all the case:


It means that the peak of perception of such a camera is really somewhere in the region of 1000-1100 microns. As expected.
The second example is more interesting. This seems to be a neutral video about the distribution of professions between Republicans and Democrats in the United States: www.youtube.com/watch?v=R34rXt_q2sY . Of course, he has a lot of comments both for and against each of the parties. Comments on complexity can be divided into three levels:
- Low. It requires only the ability to read, appeals no more than to emotions ("all XXX - %% s !!!").
- Average. It requires some knowledge of the school curriculum, tries to appeal to the facts and logic (not always correctly and not always to the right facts, but still trying).
- Tall. Requires a good knowledge of history, politics, the US economy and / or the world. Uses non-trivial logical premises.
What does theory expect? The Republican and Democratic parties are about equal in strength. Even if they wish, they are unlikely to seriously crush the opposing side on the widely visible public spot. Accordingly, the arguments “for” and “against” each party should be presented approximately evenly throughout the whole range of complexity perceived by me. Take Excel, spend three hours reading comments, and - the result:

There is a slight bias in the direction of more “stupid” arguments from the Democrats, but in general, the difference lies within the limits of statistical noise. No serious indications of the presence of censorship have been found, at least within the range of complexity available to my personal intelligence.
Take the more interesting example number 3 : “Did the Americans fly to the moon?” YouTube is our everything, here’s a video stating that lunar landings are a complete deception: www.youtube.com/watch?v=vPRyo4cSESQ . Sort comments by complexity again (I had enough pieces for 80):
- Emotions and assaults
- Requires 6-8 classes at least for the "top three".
- Without a university or specialty can not figure it out.
Result. (Pro - that the Americans were still on the moon, Con - what did not):

Och-chen interesting! Arguments “you,% spruce!” Dominate among those who believe lunar expeditions by deception. With increasing complexity (“but what about cosmic radiation?”), Their proportion noticeably decreases. Unfortunately, comments of high complexity are too few, such is the youtube audience. But even at two points there is a weighty impression that statements for the reality of flights to the moon in this video are censored. Does the author himself do this? Permissible. But much more likely is another explanation: people who do not take Moon hoax seriously simply don’t use rude and unreasonable “arguments”. A kind of internal, subculturally conditioned censorship. And, by the way, in vain. Reasoning about laser rangefinders to their opponents to the bulb because of incomprehensibility. But the simple "in our school only %%%% s still believe in Moon Hoax" may be more effective :))
Conclusion
So passive censorship is, in principle, detectable. Maximum ability to hear something through it falls on the level of complexity of messages, where its bandwidth is 37%. Quantifying the transmission curves as a function of the complexity of the incoming information, one can draw practical conclusions about the presence and strength of censorship.
Of course, the described method has a lot of disadvantages. He is subjectively dependent, he can give erroneous results with deviations from the model. Finally, it is important to remember that it is not at all quick and not cheap. Even on the measurement of the transmission curve at two points with a modest accuracy of 20% with 1σ confidence, about 50 messages are required, with the most optimistic scenario. Each of which must be read, understood, correlated with the party in the discussion and, most importantly, to assess the level of complexity. By doing this, it is necessary to manually, if you are interested in censorship is human, not automatic. This is a couple of hours of time.
So the method requires labor and patience. But if someone still seems useful or interesting - well, it means that time is spent not in vain.
Thank,
Eugene
Source: https://habr.com/ru/post/357038/
All Articles