Richard Hamming: Chapter 11. Coding Theory - II

“The goal of this course is to prepare you for your technical future.”

Hi, Habr. Remember the awesome article "You and your work" (+219, 2442 bookmarks, 393k reads)?

So Hamming (yes, yes, self-checking and self-correcting Hamming codes ) has a whole book based on his lectures. We translate it, because the man is talking.

This book is not just about IT, it is a book about the thinking style of incredibly cool people. “This is not just a charge of positive thinking; it describes the conditions that increase the chances of doing a great job. ”
')
We have already translated 25 (out of 30) chapters. And we are working on the publication "in paper."

11. Coding Theory - II

(For the translation, thanks to erosinka , who responded to my call in the "previous chapter.") Who wants to help with the translation - write in a personal or mail magisterludi2016@yandex.ru

Two things should be clear from the previous chapter. First, we want the average length L of the sent message to be as small as possible (to save resources). Secondly, this should be supported by statistical theory, since we cannot know which message will be sent, but we may know some statistical data using previous messages, and the subsequent output data may be similar to the previous ones. For the simplest theory, the only one we can discuss here, we need the probabilities of the appearance of individual characters in the message. The question of obtaining them is not part of the theory, but they can be obtained by examining past experience or imagined divination about the future use of the system you are designing.

Thus, we want instantly uniquely decoded code for a given set of input symbols, si, along with their probabilities, pi. What length li should we set (given that we have to obey Kraft's inequality) to get the minimum average code length? Huffman solved this code design problem.

Huffman was the first to show that the following inequalities must be true for a code of minimal length. If pi is in descending order, then li should be in ascending order.



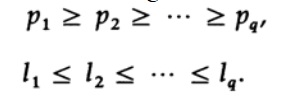
Suppose pi is in the specified order, but at least one pair li is not. Consider the effect of permuting characters associated with those two that are not in the specified order. Before permutation, the contribution of these two terms of the equation to the average code length L



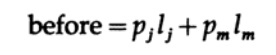
and after permutation



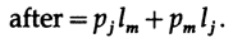
All other terms in the sum L remain the same. The difference can be written as



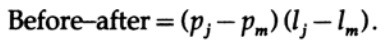
One of these terms is assumed to be negative; therefore, after rearranging two characters, the average length of the L code will decrease. Thus for the minimum code length we must have two inequalities.

Further, Huffman discovered that the code to be instantly decrypted has a decision tree, and each node must have two exits, otherwise it is an empty attempt, therefore, there are two characters with the longest length that have the same length.



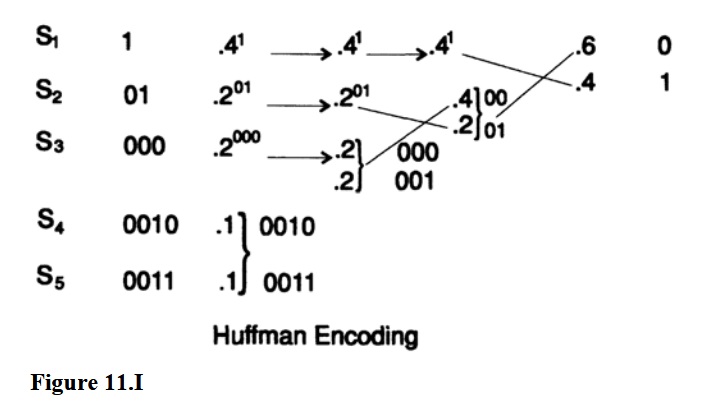
To illustrate the HUffman code, we use the classic example. Let p (s1) = 0.4, p (s2) = 0.2, p (s3) = 0.2, p (s4) = 0.1 and p (s5) = 0.1. This is depicted in Figure 11.I Then Huffman argued, based on the values ​​above, that he could combine (combine) two least frequent characters (which should have the same length) into one character with a common probability with common bits up to the last bit that is discarded, thus getting the code one character less. (?) Repeating it again and again he came to a system with two characters, for which he knew how to attribute the presentation of a code, namely one symbol - 0, and the other - 1.



Now going in the opposite direction, at each stage we need to separate the character that came out of a combination of two characters, keeping the same leading bits, but adding 0 to one character and 1 to the other. In this way we will arrive at a code of minimum length L, See Figure 11.I again. As if there were another code with a shorter length L ', then performing steps forward that change the average code length by a given number, it would come to two characters with an average code length less than 1, which is impossible . Consequently, the Huffman code has a minimum length. See Figure 11.II with the corresponding decoding tree.

This code is not unique. First of all, at each step of the process, assigning 0 and 1 to each of the characters is an arbitrary process. Secondly, if at any stage there are two symbols with the same probabilities, it does not matter which one will be the first. This may in some cases lead to the appearance of very different codes, but they both will have the same average length.

If we place the combined terms as high as possible, we get Figure 11.III with the corresponding decoding tree in Figure 11.IV. The average length of the two codes is the same, but the codes and decoding trees are different; the first is long, and the second is “branched,” and the second is less volatile than the first.

Now we will give a second example so that you can be sure of how Huffman coding works, since it is a natural desire to use a code with the shortest possible average length in the process of developing a coding system. For example, you may have a lot of data intended for storage backups, and it is known that coding it with a suitable Huffman code will save more than half the expected storage capacity. Let p (s1) = ⅓, p (s2) =, p (s3) =, p (s4) = 1/10, p (s5) = 1/12, p (s6) 1/20, p ( s7) = 1/30, p (s8) = 1/30. First we check that the sum of the probabilities is 1. The common denominator of fractions is 60. Thus, we get the total probability







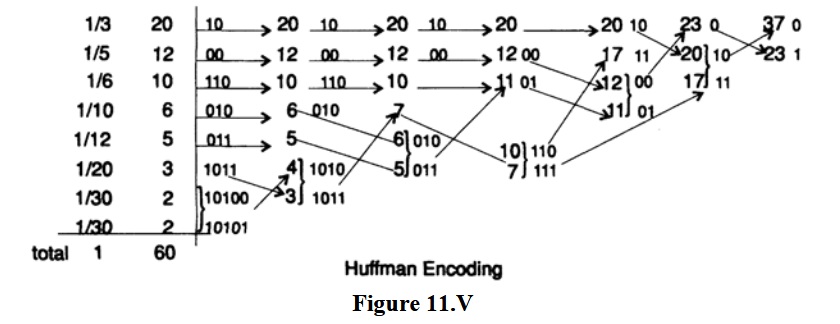
The second example is illustrated in Figure 11.V, where we omitted 60 in the denominator of probabilities, since only relative values ​​matter. What is the average code length per character? We calculate



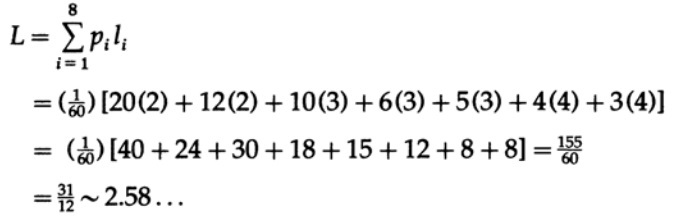
For a code block of 8 characters each character will be 3 length and the average length will be 3, which is greater than 2.58

Notice how this mechanical process is suitable for the machine. Each straight step for Huffman coding is a repetition of the same process: combine the 2 lowest probabilities, put the new amount in the right place in the array and mark it. In the reverse process, we take the marked symbol and share it. These programs are easy to write for a computer, so a computer program can calculate the Huffman code from the data si and their probabilities pi. Remember, in practice, you want to assign a return character with a very small probability, so that you can complete the decoding process at the end of the message. In fact, you can write a program that can select data for storage and find an estimate of the probabilities (small errors lead only to small changes in L), find the Huffman code, encode and send the first decoding algorithm (tree) and then the encoded data, and all this without human intervention! At the end of the decoding, you have already received a decoding tree. Thus, once having written a program, you can use it in cases where you find it useful.

The Huffman codes were used even in some computers in the instructions, since they had a very small chance of being used. Therefore, we need to look at the improvement in the average length of the L code, which we can expect when using Huffman coding, compared to simple block coding, which uses the same length for all characters.

If all probabilities are the same and there are exactly 2 ^ k characters, then a study of Huffman coding will show that you get a standard block code with the same length. If there are not exactly 2 ^ k characters, then some of them will be shorter, but it is difficult to say whether most of them will be shorter by 1 bit, or some will be shorter by 2 or more bits. In any case, the value of L will be the same, and not much shorter than in the corresponding block code.

On the other hand, if each of pi is greater than ⅔ (the sum of all subsequent probabilities, except the last), then you will get a code with a comma, in which 1 character is 1 (0) long, one character is 2 (10), and so on until end where you will have two characters of the same length (q-1): (1111 ... 10) and (1111 ... 11). In this case, the length L may be much shorter than that of the corresponding block code.

Rule: Huffman coding pays off if the probabilities of the characters are very different, and it does not pay off when they are approximately equal.

When two equal probabilities appear in the HUffman process, they can be arranged in any order, and thus the codes can be very different, although the average length of the L code in both cases will be the same. It is natural to ask what order should be chosen in the case of two equal probabilities. A reasonable criterion is to minimize the variation of the code so that messages of the same length in the original characters have approximately the same length in coded form, you do not want the original short message to be randomly encoded with a long message. The rule is simple: each new probability to insert into the table as high as possible. In fact, if you place it above the symbol with a slightly higher probability, you will significantly reduce the variation and only slightly increase L; so this is a good strategy.

After completing all the steps, we will proceed to coding the source code (although we have by no means gone through the whole topic). We turn to the coding channel with simulated noise. The channel is assumed to have noise, which means that some bits have been changed during transmission (or storage). What can be done?

Finding a single error is pretty simple. To the block of (n-1) bits you need to attach the n-th bit with such a value that all n bits have an even number 1 (or odd if you want, but we will use an even number). This is called an even parity (odd) check.

Thus, if all sent messages have this property, then at the receiving end you can check whether it is executed. If the parity check fails, it will be known that there is at least one error, in fact, an odd number of errors. Since it is prudent to use systems with a low probability of error in any position, the probability of several errors should be even lower.

For mathematical suitability, we assume that the channel has white noise, which means 1) each position in a block of n bits has the same error probability with any other position and 2) errors in different positions are uncorrelated, which means independent. With these assumptions, the error probabilities are equal



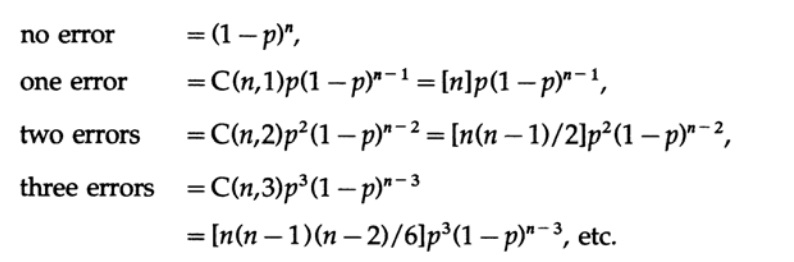
From this it follows that if, as usual, p is small relative to the length of the block n (which means the product of np is small), then multiple errors are much less likely than single errors. The choice of the length n for a given probability p is an engineering solution. If n is small, then you will have more redundancy (the ratio of the number of bits sent to the minimum possible number of bits n / (n-1)) than with a large n, but if np is large, then you will have a small redundancy, but a higher probability not detect the error. You must make an engineering decision on how to balance these two effects.
If a single error is detected, you can ask to resend the message, expecting a correct result a second time, or a third, and so on. However, if the stored message is incorrect, you will ask for a retransmission until another error occurs, and you may have two undetected errors in the single error detection scheme. Thus, retransmissions should depend on the expected nature of the errors.

Such codes were widely used even in relay times. The telephone company used code 2-of-5 in central offices and in early relay machines, which meant that only 2 out of 5 relays were in the “on” position. This code was used to represent the decimal digit, since C (5, 2) = 10. If not exactly 2 relays were in the “on” position, this meant an error, and there was a repeat. There was also a 3-out-7 code, obviously, an odd-check code.

I first met these 2-of-5 codes when using the Model 5 relay at Bell Labs, and I was impressed not only by their help in getting the right answer, but more importantly in my opinion, they gave technicians the opportunity to Actually maintain the machine. Any error was detected by the machine almost at the time of the commission, and therefore instructed the technical staff in the right direction, instead of leading them by the nose, forcing them to change the settings of the correctly working parts in an attempt to find a fault.

Violating the temporal sequence of the narrative, but remaining in the ideological, AT & T (approx. American transnational telecommunications conglomerate) once asked me how to use coding if people used an alphabet of 26 letters, 10 decimal digits and a space. This is typical of inventory naming, part naming, and many other item names, including building naming. I knew from the data on the mistakes of dialing phone numbers and from a long experience in programming that people have a pronounced tendency to rearrange adjacent numbers: 67 can become 76, as well as replacing isolated numbers (usually doubling the number: 556 will probably become 566) . Thus, the detection of one-time errors is not enough. I brought two very capable people into the meeting room and asked them a question. I rejected sentence by sentence as not good enough, until at last one of them, Ed Gilbert, proposed a weighted code. In particular, he proposed to designate the numbers 0, 1, 2, ... 36 characters 0, 1, ... 9, A, B, ..., Z, space. Then he didn’t calculate the sum of the values, but whether the kth symbol had a value (noted for convenience) Sk, then for a message of n symbols we calculate



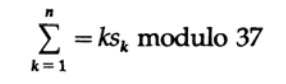
“Modulo” here means that the weighted sum is divided by 37 and only the remainder of the division is used. To encode a message of n characters, leave the first character, k = 1, empty and regardless of the remainder value, which is less than 37, subtract it from 37, and use the appropriate character to check which you need to put in the first position. Thus, the entire message with the verification character in the first position will have a verification amount equal to 0. If you consider rearranging any two different characters or replacing a single character, you will notice that this will break the weighted parity check, modulo 37 (assuming that the replaced characters are at a distance not equal to 37 characters). Without going into details, we note that it is important that the module is a simple number, which is 37.

To get a weighted sum of a symbol (in fact, their values), if you wish, you can avoid the products and use only additions and subtractions. Arrange the characters in order in the column and calculate the subtotals, then the subtotals of subtotals modulo 37, then add this to 37, and you will get a check digit. As an illustration using w, x, y, z.



On the receiving side, you re-subtract the module until you get either a-0 (the correct character) or a is a negative number (the wrong character).

If you need to use this coding, for example, to name the inventory, then if the wrong name appeared for the first time during the transfer, if not earlier (perhaps in the preliminary process), then the error will be detected, you will not have to wait until the order is will be delivered to headquarters to receive a reply later that there is no such name, or to receive an incorrect order. The error will be detected before the order leaves you and therefore it is easy to fix. Simply? Yes! Effectively against human error (as opposed to the white noise example), yes!

Indeed, these days you can see a similar code on books with an ISBN number. This is the same code, only it uses 10 decimal digits, and the number 10 is not a prime number, so they had to enter the 11th character X, which may appear at times during a parity check - indeed, approximately every 11th book will be have X as the last character in the ISBN parity number. Dash mainly perform a decorative function and are not used in coding. Check it yourself on your textbooks. Many other large organizations could use such codes for good effect if they wanted to make an effort.

I have repeatedly pointed out that I believe that in the future information in the form of symbols will be important, and material things will be less important, and therefore, the theory of coding (representing) information into convenient codes is a non-trivial topic. The material above gives simple error detection code for machines, and weighted code for human use. These are just 2 examples of how coding theory can help in situations where machine and human error is possible.

When you think about the human-computer interface, one of the things that can be useful to you is the need to make as few keystrokes as possible with a person — Huffman coding under cover! Obviously, given the probabilities of various branches in the program menus, you can, if you wish, think up a way to reduce the total number of keystrokes. Thus, the same menu set can be customized to the habits of different people, instead of offering everyone the same interface. In a broader sense, “automated programming” in high-level languages ​​is an attempt to achieve something like Huffman coding, to use relatively few keystrokes to solve desired tasks, and to use other keys for other tasks.

To be continued...

Who wants to help with the translation, layout and publication of the book - write in a personal or mail magisterludi2016@yandex.ru

By the way, we also started the translation of another cool book - “The Dream Machine: The History of Computer Revolution” )