Richard Hamming: Chapter 12. Error Correction Codes

“The goal of this course is to prepare you for your technical future.”

Hi, Habr. Remember the awesome article "You and your work" (+219, 2442 bookmarks, 394k readings)?

So Hamming (yes, yes, self-checking and self-correcting Hamming codes ) has a whole book based on his lectures. We translate it, because the man is talking.

This book is not just about IT, it is a book about the thinking style of incredibly cool people. “This is not just a charge of positive thinking; it describes the conditions that increase the chances of doing a great job. ”
')
We have already translated 26 (out of 30) chapters. And we are working on the publication "in paper."

Chapter 12. Error Correction Codes

(Thanks for the translation thanks to Mikhail Sheblaev, who responded to my call in the “previous chapter.”) Who wants to help with the translation - write in a personal or mail magisterludi2016@yandex.ru

Two topics are covered in this chapter: the first is obviously error correction codes, and the second is how the opening process sometimes happens. As you all know, I am the official discoverer of Hamming codes with error correction. Thus, I, apparently, have the opportunity to describe how they were found. But you need to beware of any stories of this type. In truth, at that time I was already very interested in the discovery process, believing in many cases that the discovery method is more important than what is open. I knew enough not to think about the process during research, just as sportsmen do not think about technology when they compete, but work it out to automatism. I also developed the habit of going back after big or small discoveries and trying to track down the steps that led to them. But do not be deceived; At best, I can describe the conscious part and the small tip of the subconscious part, but we simply do not know the magic of the work of the subconscious.

I used the Model 5 relay computer in New York, preparing it for sending to Aberdeen Proving Grounds along with some of the software required (mainly math programs). If an error was detected with the help of 2-of-5 block codes, the machine left unattended could repeat an erroneous cycle up to three times in a row before discarding it and taking on a new task, hoping that the problematic equipment would not be involved in the new solution. At that time, as they say, I was a junior janitor's senior assistant, I only got free machine time on weekends - from 17-00 Fridays to 8-00 Mondays - it was a lot of time! So I could load the input tape with a lot of tasks and promise my friends, returning to Murray Hill, New Jersey, where the research department was located, that I would prepare answers by Tuesday. Well, one weekend, as soon as we left on Friday evening, the car broke down completely and I had absolutely nothing by Monday. I had to apologize to my friends and promise them answers by the following Tuesday. Alas! The same situation happened again! I was mildly angry and exclaimed: “If the machine can determine that an error exists, why doesn’t it determine where the error is and fix it by simply changing the bit to the opposite?” (Actually, the expressions used were a little stronger!).

We note first of all that this significant shift occurred only because I was experiencing tremendous emotional stress at that moment and this is typical of most great discoveries. Calm work will allow you to improve and develop ideas in more detail, but a breakthrough usually comes only after a lot of stress and emotional involvement. Calm, cold, not involved researcher rarely takes really big new steps.

Let's return to the story. I knew from previous discussions that, of course, it would be possible to construct three instances of the calculator, including comparing schemes, and to use error correction by the method of majority voting. But what would it cost! Of course, there were better methods. I also knew, as discussed in the previous chapter, about the cool thing with parity. I understood their structure very carefully.
Pasteur, on the other hand, said: "Good luck loves the prepared." As you can see, I was prepared by my previous work. I knew more than well the 2-of-5 coding, I understood them fundamentally and worked and understood the general effects of parity.



Fig. 12.I

After some reflection, I realized that if I positioned the bits of any message symbol in the form of a rectangle and write down the parity of each column and each line, the two not passed parity checks will show me the coordinates of one error and this will include the angular added parity bit (which could be set accordingly , if I had odd values) Pic. 12.I. Redundancy, the ratio of what you use, to the minimum required quantity, is



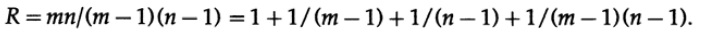
Anyone who has studied mathematical analysis, it is obvious that the closer a rectangle is to a square, the less redundancy there is for a message of the same size. And, of course, large values ​​of m and n would be better than small ones, but then the risk of double error would be great from an engineering point of view. Note that if two errors occur, then you have: (1) if they are not in one row or column, then just two rows and two columns contain errors and we do not know which diagonal pair caused them; (2) if two errors happened in one row (or column), then you have only one column (row) and not a single row (column).

Fast forward a few weeks later. To get to New York, I had to get a little earlier to Murray Hill, New Jersey, where I worked, and take a ride on a mail delivery machine for the company. Well, yes, a trip through northern New Jersey in the early morning is not very picturesque, so I made a habit of revising my achievements, so the pen spun in my hands automatically. In particular, I twisted rectangular codes in my head. Suddenly, and I don’t know the reasons for this, I found that if I take a triangle and place parity bits on the diagonal so that each bit checks the column and row at the same time, I will get more acceptable redundancy, Figure 12.II.

My complacency in an instant disappeared! Did I get the best code this time? After a few miles of thinking about this (remember, nothing distracts the landscape of northern New Jersey), I realized that a cube of information bits with parity on each plane and parity on the axes, on all three axes, would give me three coordinates for error at the cost of only 3n-2 parity checks for a coded message of length n ^ 3. It is better! But was this the best decision? Not! Being a mathematician, I quickly realized that a 4-dimensional cube (I should not have placed the bits like that, just to designate internal connections) would be even better. Thus, even a higher dimension would be even better. It soon became clear (say, after 5 miles) that a cube of dimension 2x2x2x ... x2 with n + 1 parity would be better - obviously!



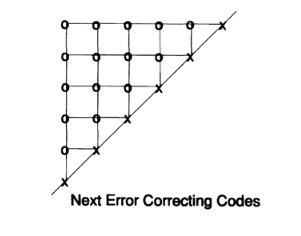
But once having burned my fingers, I was not going to agree with what looked good - I had already made this mistake before! Could I prove that this was the best solution? How to prove it? One obvious approach was to try to calculate the parameters, I had n + 1 control bits displayed on a string of n + 1 bits, i.e. binary number of length n + 1 bits, and this could represent an arbitrary object of length 2 ^ {n + 1}. But I only needed 2 ^ n + 1 bits, 2 ^ n points in the cube, plus one bit, confirming that the message was correct. I did not take into account almost half of the bits. Alas! I arrived at the door of the company, registered and went to the conference, giving the idea to rest.

When I returned to the idea after several days of distracting events (after all, it was assumed that I contributed to the company's team effort), I finally decided that a good approach would be to use error syndrome as a binary number indicating the location of the error, with, of course, all zero bits in case of correct result (easier test than for all units on most computers). Note, familiarity with the binary system, which was not then common (1947-1948) has repeatedly played a prominent role in my constructions. This is a fee for knowing more than is needed momentarily!
How do you construct this particular case of error correction code? Easy! Write the positions in binary code:



Now it is obvious that the parity check in the right half of the syndrome should include all positions having 1 in the right column; the second number on the right should include numbers with 1 in the second column, etc. Therefore you have:



Thus, if an error occurs in a certain discharge, the corresponding parity checks (and only these) will fail and give 1 in the syndrome, this will be exactly the binary representation of the error position. It's simple!

To see the code in action, we will limit ourselves to 4 bits for messages and 3 control positions. These numbers satisfy the condition



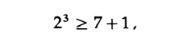
which is obviously a necessary condition, and equality is sufficient. Choose for the position of the check bits (so that the parity is easier) check bits 1, 2 and 4. Positions for the message - 3, 5, 6 7. Let the message be

1001

We (1) write the message in the top line, (2) encode the next line, (3) insert the error in position 6 on the next line and (4) on the next three lines, we calculate three parity checks.



Let's apply parity checks to the received message:



The binary number 110 is> 6, hence change to position 6, drop the control bits 1, 2 and 4 and you will get the original message, 1001.

If this seems like magic, think about the message of all 0, which will have control positions at 0, and then imagine changing one bit and you will see how the error position moves, and then the binary number of the syndrome will change accordingly and correspond exactly to the error position. Then note that the sum of any two valid messages is still a valid message (parity checks are modulo 2 additive, hence the correct messages form an additive modulo group 2). The correct message will give all zeros, therefore the sum of correct messages plus a single-bit error will give the error position regardless of the message being sent. Parity checks focus on the error and ignore the message.

Now it is immediately apparent that any exchange of any two or more of the columns once matched at each end of the channel will have no significant effect; the code will be equivalent. Similarly, a permutation of 0 and 1 in any column will not give significantly different codes. In particular, the (so-called) Hamming Code is simply a nice reordering, and in practice you could check the check bits at the end of the message, rather than scatter them in the middle of the message.

How about a double mistake? If we want to catch (but not correct) a double error, we simply add a single new parity check to the whole message that we send. Let's see what happens at your end of the channel.



Correcting single errors plus detecting double errors is often a good balance. Of course, redundancy in a short message of 4 bits, now with 4 check bits, is bad, but the number of check bits grows (roughly) as a logarithm of the message length. A message is too long - and you risk getting a double uncorrectable error (which you “correct” in the third error with a single error correction code), too short a message - and the cost of redundancy is too high. Again, engineering reasoning, depending on the case ...

From analytic geometry you have learned the significance of using complementary algebraic and geometric representations. The natural representation of a string of bits should use an n-dimensional cube, each row of which is the vertex of the cube. Using this picture and finally noticing that any one error in the message moves the message along one edge, two errors along two edges, etc., I slowly realized that I had to act in the $ L_1 $ space. The distance between elements is the number of digits in which they differ. Thus, we have a metric on space and it satisfies three standard distance conditions (see Chapter 10 for the standard distance in L_1).



Thus, I had to take seriously what I knew as an abstraction of the Pythagorean function of distance.

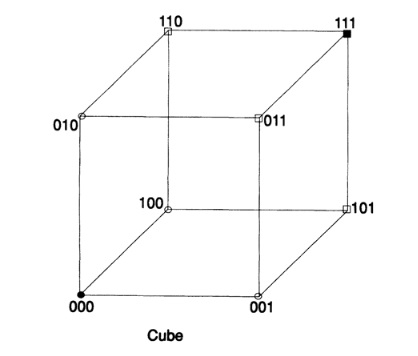
Having the concept of distance, we can define a sphere as all points (vertices, since everything is considered in a set of vertices), at a fixed distance from the center. For example, in a 3-dimensional cube that can be easily drawn, Fig. 12.III, the points (0,0,1), (0,1,0), and (1,0,0) are at a unit distance from (0,0,0), while the points (1, 1,0), (1,0,1), and (0,1,1) are at a distance of 2 further, and finally the point (1,1,1) is at a distance of 3 from the origin.

We now move to the space with n dimensions and draw a sphere of unit radius around each point and assume that the spheres do not intersect. Obviously, the centers of the spheres are code elements and only these points, then the result of receiving any single error in the message will be a “non-code” point and you can understand where this error came from. It will be inside the sphere around the code point I sent you, which is equivalent to a sphere of radius 1 around the code point you received. Therefore, we have an error correction code. The minimum distance between code points is 3. If we use non-intersecting spheres of radius 2, then the double error can be corrected, because the resulting point will be closer to the original code point than to any other point; the minimum distance for double correction is 5. The following table shows the equivalence of the distance between code points and error “correctability”:



Thus, the construction of a code with error correction is exactly the same as the construction of a set of code points in n-dimensional space



which has the necessary minimum distance between legal messages, since the conditions above are necessary and sufficient. It should also be clear that we can exchange error correction for their detection — refuse to correct one error and you will get two more instead.

Earlier, I showed how to develop codes that satisfy the conditions in the case when the minimum distance is 1.2, 3 or 4. Codes with large minimum distances are not easily described and we will not go further in this direction. It is easy to find the upper estimate of how large the code distances can be. It is obvious that the number of points in the sphere of radius k is (C (n, k) is the binomial coefficient)



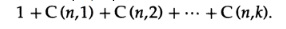
Therefore, if we divide the volume of the whole space, 2 ^ n, by the volume of the sphere, then the quotient will be an estimate from above of the number of non-intersecting spheres, i.e. points of code in the appropriate space. To get additional error detection, we still add a full parity check, thus increasing the minimum distance, which was 2k + 1, to 2k + 2 (since any two points at the minimum distance will have the same parity, we will increase the minimum distance by 1 ).

Let's summarize where we are now. We see that with proper code building we can create a system of unreliable parts and get a much more reliable machine, and we see how much we have to pay for this equipment, although we didn’t research the cost of computation speed if we create a computer with this level of error correction. But I previously mentioned another benefit, namely maintenance during operation, and I would like to remind you of it again. The more sophisticated the equipment, and we are obviously moving in this direction, the more vital is the operational maintenance, error correction codes mean that the equipment will not only give (possibly) correct answers, but can also be successfully served by low-skilled personnel.

The use of error detection codes and error correction codes is constantly growing in our society. Sending messages from spacecraft sent to distant planets, we often have 20 watts of power or less (maybe even 5 watts) and use codes that correct hundreds of errors in one message block — correction is made on Earth, of course. When you are not ready to overcome the noise, as in the situation described above or in the case of an “intentional congestion,” such codes are the only known way out.

In the late summer of 1961, while I was on a professorship, I drove across the entire country from Stanford, California to Bell Telephone Laboratory in New Jersey. I planned a stop in Morris, Illinois, where the telephone company installed the first electronic telephone station, which was no longer experimental. I knew that the station was actively using Hamming codes and, of course, I was invited. I was told that the installation had never been as easy as this. I said to myself: “Of course, this is what I have been preaching for the past 10 years.” When during the initial setup all modules are installed and working properly (and in some sense you know that this is due to self-checks and adjustments), and you turn to go to the next steps if something goes wrong, equipment will just tell you about it! The ease of initial installation, as well as subsequent maintenance, was simply visible to the naked eye! I can not exaggerate, the correction of errors not only led to the correct results during the work, but when applied correctly, significantly contributed to the installation and maintenance on site. And the more sophisticated the equipment, the more important these things are!

I want to refer to another part of this chapter.I carefully told you a lot of what I encountered at each stage in the detection of error correction codes, and what I did. I did this for two reasons. First, I wanted to be honest with you and show you how easy it is to follow Pasteur’s rule “Luck smiles prepared”, to succeed, just preparing yourself for success. Yes, there were elements of good luck in discovery; but in almost the same situation there were many other people, and they did not do it! Why me? Good luck, to be sure, but I also prepared myself to understand what was happening - more than other people around, just reacting to the phenomena when they occurred, and not thinking deeply about what was hidden under the surface.

I now challenge you. What I wrote down on several pages was done for a total of about three to six months, mostly working days, at the moments of the usual performance of my work duties in the company. (Patenting delayed publication for more than a year). Can anyone say that he, in my place, could not have done this? Yes, you were just as capable as I was to do it - if you were there, and you prepared as well!

Of course, living your life, you do not knowwhat to prepare for - you want to accomplish something significant and not spend your whole life being a “doorman of science” or what else you do. Of course, luck plays a prominent role. But as far as I can see, life gives you many, many opportunities to do something big (define it as you want) and a prepared person usually succeeds one or several times, and an untrained person will fail almost every time.

The aforementioned opinion is not based on this experience, or simply on my own events, it is the result of studying the lives of many great scientists. I wanted to be a scientist, therefore I studied them, and I studied the discoveries that happened where I was, I asked questions to those who did it. This opinion is also based on common sense. You grow in yourself a style of accomplishing great accomplishments, and then, when the opportunity is found, you almost automatically react with the maximum steepness in your actions. You have trained yourself to think and act in the proper way.

There is one nasty thesis that needs to be mentioned, however, that being great in an era is not something that needs to be clarified in subsequent years.. Thus, preparing yourself for future great accomplishments (and their ability is more common and easier to achieve than you think, since you do not often recognize big accomplishments when it happens under your nose), you need to think about the nature of the future in which you will live. The past is a partial guide, and the only thing you have besides history is the constant use of your own imagination. Again, a random search of random decisions will not lead you anywhere as far as decisions made with your own vision of what your future should be.

I told and showed you how to be great; now you have no excuse for not doing this!

To be continued...

Who wants to help with the translation, layout and publication of the book - write in a personal or mail magisterludi2016@yandex.ru

By the way, we also started the translation of another cool book - “The Dream Machine: The History of Computer Revolution” )