Again about the trees
Spring, it's time to think about the trees. Trees in relational - DB is one of the most sensitive issues when working with data. In this topic, we will compare the performance of the Materialized Path and Adjacency List methods using the “explain analize” command.
The other day I was interviewed in one good company and came to the conclusion that not everyone is ready to study the subject with which they work more thoroughly. Namely, the fact that sometimes an implicit and incorrect at first glance decision may be the most correct.
I decided to understand in a little more detail what the problem is and test the two most simple options. Materialized Paths (MP) and Adjacency List (AL). Nested Sets I do not consider in view of the purpose of this topic. And its goal is to compare the choice of parentId_parentId_parentId and the choice: pid numbers.
It would seem that the fastest choice will be by number. But let's take a closer look. Very rarely we need to choose a separate branch without heirs. Very often, the number of nesting or just the number of the heir is not controlled.
')
Therefore, I took several different parent branches with nesting in 5 levels with 10-30 elements in each node. Got a little less than a million entries. It is working figures for not too active blog, email client, etc.
Create a table tree and indexes to it for two types of tree at the same time (for the purity of the experiment.
The most attentive noticed a strange field btree. We speak abstractly and we do it optimized.
So, we have created a conditional tree, two fields for different methods and a unique identifier. Add data to it for example as follows:
Here I deliberately did not want to bother with recursions, therefore I wrote like this. Initially I wanted to recursively do it, and then I thought that this was a topic for a separate topic, and left it as it is.
Requests I performed easier. Opened pgAdmin4 and launched EXPLAIN ANALYZE with the Cost and timing flags turned on.
And we were interested in two requests.
For MP:
For AL:
Where: pid - id of the parent.
The request for the AL method is very, very confusing. And this query will have to be used quite often.
I will remove the sorting from the result; it is performed in both requests for a comparable time, and it is large enough, and without it the result will be more impressive.
Here are beautiful pictures:
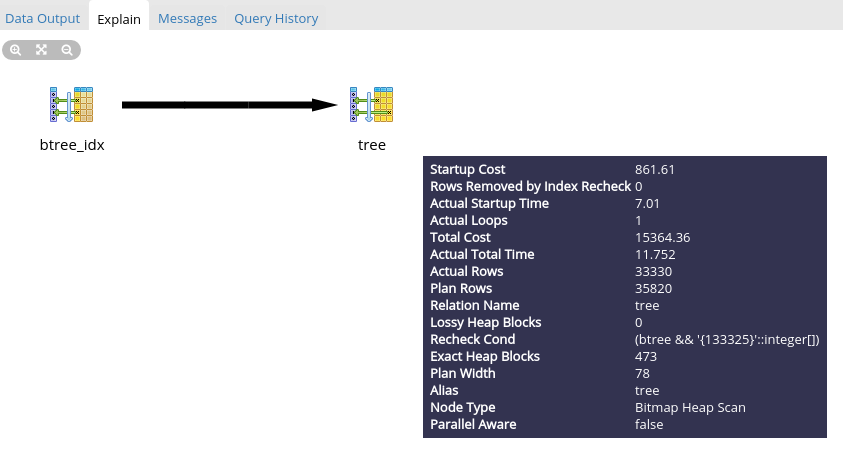
It's simple, but for MP. Look at the request for AL:

Already more beautiful, but we see that MP’s Total Cost is one and a half times larger ... And all because our index does not store numbers, but an array of numbers. But despite this, as a result, MP’s execution speed is much higher. And the more nestings and the number of parent elements, the greater the difference in speed.
In addition, the simplicity of sampling from requests with ease allows you to collect data through the ORM system in one request. A big disadvantage of MP is a more complex method of transferring data from one branch to another, but nonetheless fairly transparent. But such operations are usually not of a mass nature and it is not quite right to focus on this with such a difference in performance.
In the screenshots all the data is relevant, it is not the peak values, but quite average. But even at peak values, the difference in speed is at least 5 times (the slowest MP and the fastest AL method.
Agree, a very good bonus for those who really want to understand everything.
The other day I was interviewed in one good company and came to the conclusion that not everyone is ready to study the subject with which they work more thoroughly. Namely, the fact that sometimes an implicit and incorrect at first glance decision may be the most correct.
I decided to understand in a little more detail what the problem is and test the two most simple options. Materialized Paths (MP) and Adjacency List (AL). Nested Sets I do not consider in view of the purpose of this topic. And its goal is to compare the choice of parentId_parentId_parentId and the choice: pid numbers.
It would seem that the fastest choice will be by number. But let's take a closer look. Very rarely we need to choose a separate branch without heirs. Very often, the number of nesting or just the number of the heir is not controlled.
')
Therefore, I took several different parent branches with nesting in 5 levels with 10-30 elements in each node. Got a little less than a million entries. It is working figures for not too active blog, email client, etc.
Create a table tree and indexes to it for two types of tree at the same time (for the purity of the experiment.
-- Table: public.tree -- DROP TABLE public.tree; CREATE TABLE public.tree ( id integer NOT NULL DEFAULT nextval('tree_id_seq'::regclass), name text COLLATE pg_catalog."default", pid integer, btree integer[] ); -- Index: btree_idx -- DROP INDEX public.btree_idx; CREATE INDEX btree_idx ON public.tree USING gin (btree); -- Index: pid_idx -- DROP INDEX public.pid_idx; CREATE INDEX pid_idx ON public.tree USING btree (pid); The most attentive noticed a strange field btree. We speak abstractly and we do it optimized.
So, we have created a conditional tree, two fields for different methods and a unique identifier. Add data to it for example as follows:
// Generate ... func (c *TreeController) Generate() { for i := int64(0); i < 10; i++ { pidStr := "" cur_i_id, _ := c.GenerateRecurse(0, pidStr) for j := 0; j < 30; j++ { pidStr := strconv.Itoa(int(cur_i_id)) cur_j_id, _ := c.GenerateRecurse(cur_i_id, pidStr) for z := 0; z < 10; z++ { pidStr := strconv.Itoa(int(cur_i_id)) + "," + strconv.Itoa(int(cur_j_id)) cur_z_id, _ := c.GenerateRecurse(cur_j_id, pidStr) for z1 := 0; z1 < 10; z1++ { pidStr := strconv.Itoa(int(cur_i_id)) + "," + strconv.Itoa(int(cur_j_id)) + "," + strconv.Itoa(int(cur_z_id)) cur_z1_id, _ := c.GenerateRecurse(cur_z_id, pidStr) for z2 := 0; z2 < 10; z2++ { pidStr := strconv.Itoa(int(cur_i_id)) + "," + strconv.Itoa(int(cur_j_id)) + "," + strconv.Itoa(int(cur_z_id)) + "," + strconv.Itoa(int(cur_z1_id)) c.GenerateRecurse(cur_z1_id, pidStr) } } } } } } // GenerateRecurse ... func (c *TreeController) GenerateRecurse(pid int64, treepid string) (int64, error) { v := models.Tree{ Name: "test -- " + treepid, Pid: pid, Btree: "{" + treepid + "}"} return models.AddTree(&v) } Here I deliberately did not want to bother with recursions, therefore I wrote like this. Initially I wanted to recursively do it, and then I thought that this was a topic for a separate topic, and left it as it is.
Requests I performed easier. Opened pgAdmin4 and launched EXPLAIN ANALYZE with the Cost and timing flags turned on.
And we were interested in two requests.
For MP:
SELECT * FROM tree WHERE btree && ARRAY[:pid] ORDER BY array_length(btree, 1); For AL:
WITH RECURSIVE nodes(id,name,pid, btree) AS ( SELECT s1.id, s1.name, s1.pid, s1.btree FROM tree s1 WHERE pid = :pid UNION SELECT s2.id, s2.name, s2.pid, s2.btree FROM tree s2, nodes s1 WHERE s2.pid = s1.id ) SELECT * FROM nodes order by pid asc; Where: pid - id of the parent.
The request for the AL method is very, very confusing. And this query will have to be used quite often.
I will remove the sorting from the result; it is performed in both requests for a comparable time, and it is large enough, and without it the result will be more impressive.
Here are beautiful pictures:

It's simple, but for MP. Look at the request for AL:

Already more beautiful, but we see that MP’s Total Cost is one and a half times larger ... And all because our index does not store numbers, but an array of numbers. But despite this, as a result, MP’s execution speed is much higher. And the more nestings and the number of parent elements, the greater the difference in speed.
In addition, the simplicity of sampling from requests with ease allows you to collect data through the ORM system in one request. A big disadvantage of MP is a more complex method of transferring data from one branch to another, but nonetheless fairly transparent. But such operations are usually not of a mass nature and it is not quite right to focus on this with such a difference in performance.
In the screenshots all the data is relevant, it is not the peak values, but quite average. But even at peak values, the difference in speed is at least 5 times (the slowest MP and the fastest AL method.
Agree, a very good bonus for those who really want to understand everything.
Source: https://habr.com/ru/post/354694/
All Articles