A little about physics in almost Agar IO on aicups.ru

In the MiniAICup competition # 2, Almost Agar IO, you need to control amoebas, eat food and other amoebas.
For the implementation of the amoeba control algorithm, potential fields are suggested, but there is one big BUT.

The physics of movement in the game are defined by the following equations:

speed_x + = (nx * max_speed - speed_x) * INERTION_FACTOR / mass;
speed_y + = (ny * max_speed - speed_y) * INERTION_FACTOR / mass;

It turns out physics with friction and inertia, which spoils everything. If the physics are not taken into account, and the force vector (nx) is directed directly to the nearest target, it turns out like this:


')
For optimal eating of food and opponents you need to take these equations into account.

To start, bring them into a convenient vector view:

$$$$ display $$ \ vec V_n = \ vec V_ {n-1} + (\ vec \ varphi * V_m - \ vec V_ {n-1}) * \ mu \\ \ vec X_n = \ vec X_ {n- 1} + \ vec V_n \\ \ varphi - \ textrm {force vector (remember that its module is 1)} \\ V_m - \ textrm {maximum speed} \\ \ mu - \ textrm {INERTION_FACTOR} / mass $$ display $$

So, there is a field with food. On the field own amoeba with known coordinates and speed. It is necessary to calculate in which direction to apply a force vector in order to eat food as quickly as possible.

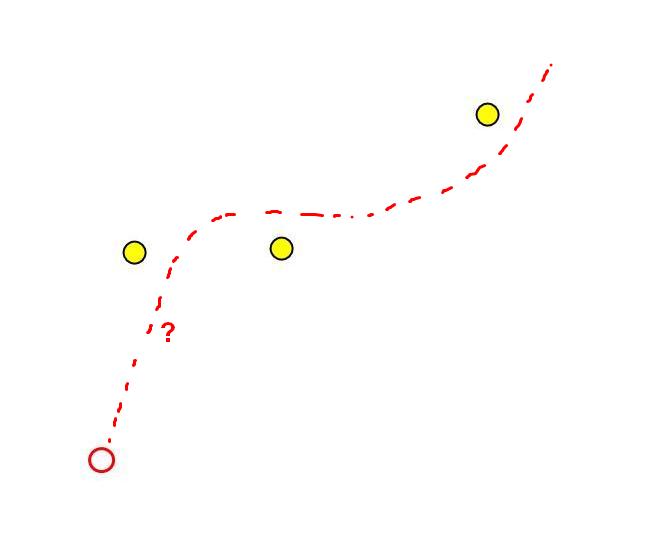
Calculation of motion paths

The most obvious option is this:
We assume that for the next T steps we will not change the force vector φ, choose K directions of force application and calculate the trajectory of movement in each direction. At each point of the trajectory we see whether it is possible to eat food.



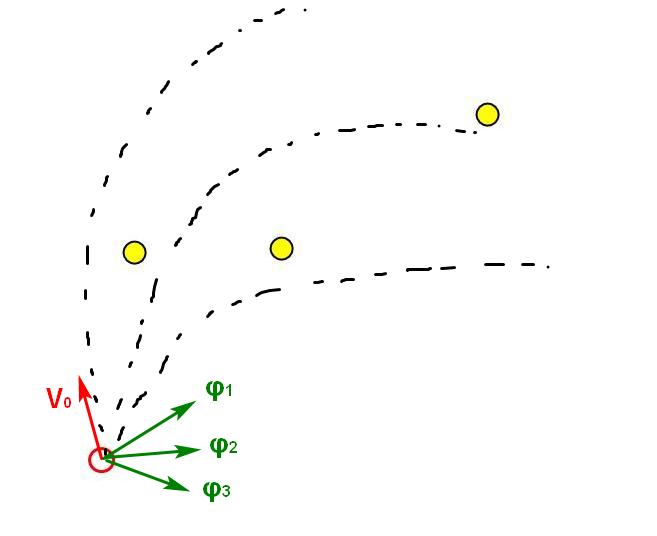
Having the above equations, the calculation of trajectories is done very easily and quickly, but the complexity of this approach grows very quickly. At each point of each trajectory, it is necessary to consider whether each amoeba reaches each food.

We have:

• K trajectories
• P pieces of amoeba
• S food
• T steps of the trajectory

All these numbers are multiplied. When the amoeba is divided into several parts, when they have a large viewing radius, they see a lot of food, the calculation algorithm ceases to fit into the 20 ms allocated for the calculations.

Nevertheless, such an algorithm for finding food with some optimizations easily fits into the top 52.

Analytical solution of the equations of motion

Having the initial values ​​of V0 and X0, you can calculate any point of the trajectory immediately at the n-th step.

The equations of motion by simple transformations turn into this:

$$

$$\ vec V_n = \ vec \ varphi * V_m + (\ vec V_0 - \ vec \ varphi * V_m) * (1- \ mu) ^ n \\ \ vec X_n = \ vec X_0 + \ vec \ varphi * n * V_m + (\ vec V_0 - \ vec \ varphi * V_m) * (1- \ mu) * \ frac {1 - {(1- \ mu)} ^ n} {\ mu}$$

Do not be scared. It looks scary, especially the equation for the coordinate, but it is easy to calculate. Here, Vn and Xn depend only on the initial conditions X0 and V0 of time.

Having these equations, you can immediately try to derive at what step n, the distance to the pre-specified food will be minimal.



Such an approach would greatly save computing resources. There would be no need to calculate the distance from each meal to each point of the trajectory.

But I didn’t work out analytically the number of such a point. Therefore, I used the golden section algorithm to search for a point that has the minimum distance to a given food.

At a path length of 100 ticks, this approach requires calculating only 10 points to find the closest one to the food.

However, tests have shown that the first described method requires less time to calculate for trajectories with a length of <100 ticks. Maybe because of the used lambda or maybe because of some kind of error.

Reachable areas

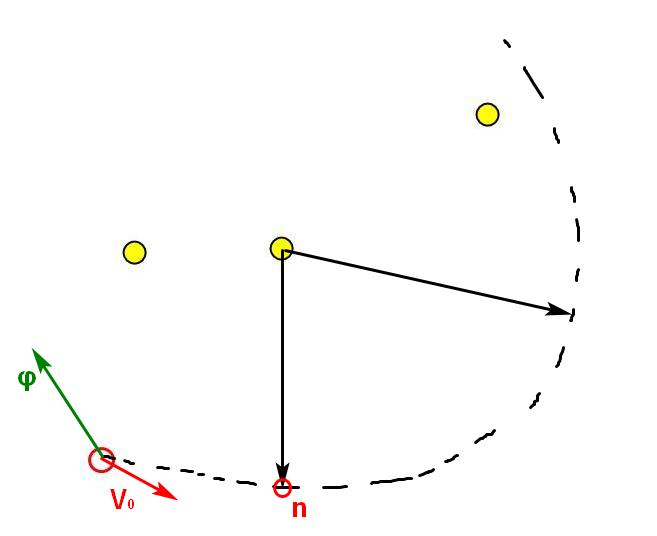
If you look closely at the coordinate equation in the nth step, you will notice:

$$

$$\ vec X_n = \ vec X_0 + \ vec V_0 * crap (n) + \ vec \ varphi * other fuck (n)$$

Remember that the module of force φ is equal to one.

It turns out that wherever the force φ is directed, after a time n the amoeba will be on the circle (if the force is always directed in one direction during all steps n), or inside the circle (if the direction of the force changes during n steps).

Center and radius of the circle:

$$

$$\ vec O_n = \ vec X_0 + \ vec V_0 * crap (n) \\ R_n = \ vec \ varphi * other fuck (n)$$

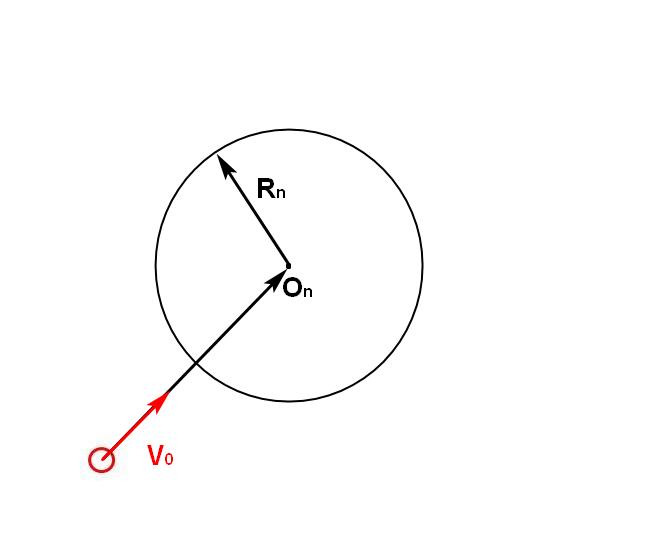
This is the reachable area! In n steps, an amoeba will surely be either inside this area or on its border!

How do we use it?

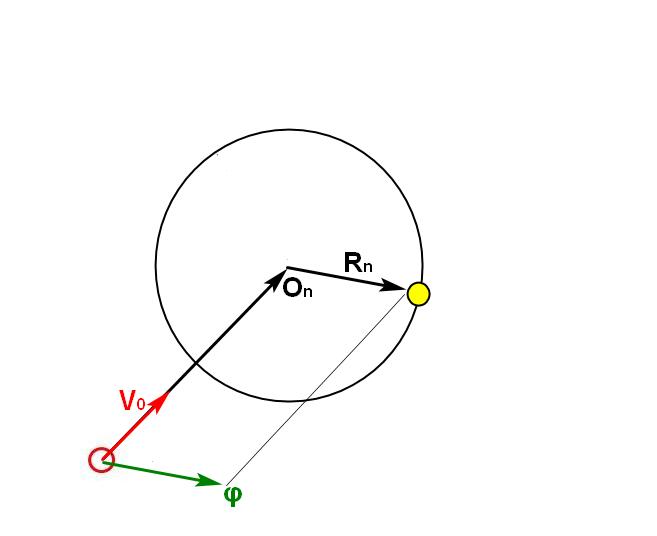
Guidance on food

We need to find such a step n, at which the boundary of the reachability area will touch the food. Take the vector from the center of the reachability area to the food. This will be the desired direction of force, setting which amoeba as quickly as possible comes to food.

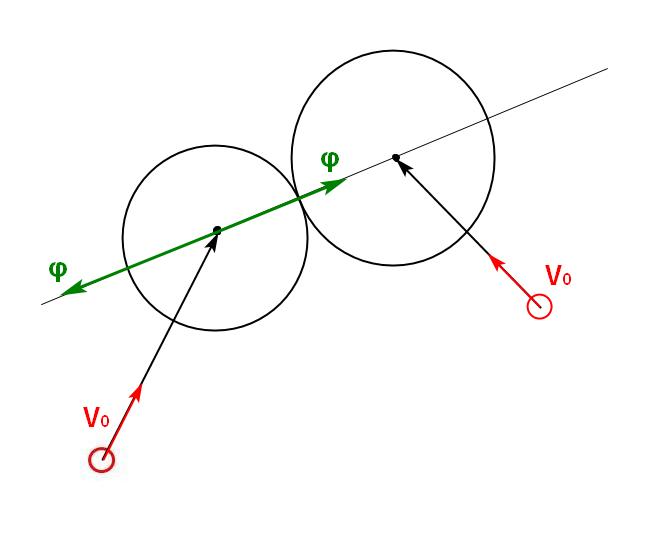
Guiding and avoiding enemies

The enemies also have their own reachability. It is necessary to find a step in which its own and enemy areas of reachability come into contact. If you need to catch up with the enemy, then the force vector must be directed along the line connecting the centers of the two reachable areas.

If it is necessary to run away, then the force vector should be directed in the opposite direction.