Uncountable: in search of a finite number

The ancient Greeks - adherents of concepts that have a strict logical sense - avoided the concept of infinity in every way. Indeed, what do we care about an infinite series of numbers, if neither we can write down or present it?

In the Middle Ages, logical rigor was discarded for the sake of mathematical results and developed extremely efficient algorithmic methods operating in infinity calculations.
')
In the XX century. another problem began to show through clearly. We can deal with infinity with the help of one symbol (∞), but what to do with numbers that are less than infinity, but at the same time unimaginably huge?

We came close to the numbers, barely inferior to the “Ouroboros”, but still having theoretical and practical significance. You could probably hear about the Graham number, which is the upper limit for solving a particular problem in Ramsey’s theory. 88 years after the appearance of the Ramsey theorem, mathematics are ready to discard the old methods and go even further.

Welcome to the rabbit hole without a bottom.

Entry in which you need to remember the past

In the XVII century. mathematician and philosopher Blaise Pascal wrote about his fear of infinity, about his own insignificance at the thought of the vast expanses of the cosmos. Interestingly, what would Pascal say about the Graham number, consisting of a tower of numbers high from the Earth to the most distant star, each number of which hides its own tower of numbers? Each bend of a number in a tower of numbers, which consists of a tower of numbers, contains in itself a tower of other numbers - but even with this formulation we didn’t come close to the discovery made by Graham.

The origins of the Graham number should be sought in 1928, when a young mathematician Frank Ramsay noticed an amazing thing while working on an article on logic: complete disorder is impossible. Each sufficiently large set of numbers, points, or objects necessarily contains a highly ordered structure.

Guessing, which was only a small part of the work on logic, marked the beginning of a completely new field of mathematics, called Ramsey theory. It is often explained with the example of a party: suppose you want to find the perfect balance between those who know each other and strangers. You draw a map of the relationships of all your friends, connecting two people if they are friends, a blue line, and a red line - if they are not familiar with each other. Then a similar illustration might come out:



The beauty of Ramsey’s theory is that the tasks in this area are always very easy to formulate . Considering the example of a party, it is very interesting to understand how many people are enough to form a group in which there will always be four people either friends or not friends with each other.

In the group of 17 points shown in the figure above, it is impossible to find four points for which the network of edges connecting them would be entirely red or blue. Therefore, more than 17 people are required, so that among them there must be four people who are familiar or not familiar with each other. In fact, in a group of 18 people there will always be either four acquaintances, or four not familiar with each other.

Take any star cluster. It is always possible to find a group in it, which with a very high accuracy forms any given configuration - a straight line, a rectangle, a bucket.

Mathematicians are trying to figure out how large the set of stars, numbers, or any objects must be in order to guarantee the existence of a certain desired substructure. Decisions on such tasks often take decades.

The Ramsey theory is also of great practical importance - from organizing a good party to building more advanced communication networks and information transmission and retrieval systems. In fact, it is very difficult to imagine for what purposes many of the methods developed for solving problems in Ramsey theory can serve - this is the most advanced edge of mathematics.

How and why did Graham come to his number

The American mathematician Ronald Lewis Graham (born 1935) made a significant contribution to discrete mathematics. Graham - a versatile personality. At one time he was even president of the international association of jugglers, but became famous solely due to a large positive integer number, which serves as the upper boundary of a specific problem in Ramsey theory.


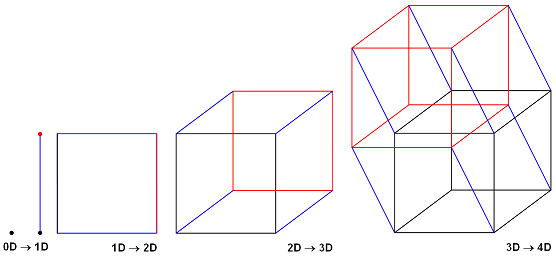
An n-dimensional cube always contains 2n vertices. Despite their dimension, n-dimensional cubes are simply graphs whose vertices are connected by edges.

We can turn any n-dimensional cube into a complete graph simply by connecting all the vertices. The remaining edges thus formed are inside or on one of the faces. Imagine that these edges have two colors - red and blue. Thus, Graham formulated an interesting question that lies in the plane of the classical Ramsey theory: at what minimum value N of a two-color k-dimensional cube each such coloring necessarily contains a complete subgraph painted with one color, with four vertices, each of which lies in the same plane?


Full graph on a three-dimensional cube with two-color ribs

In 1971, Ronald Graham and Bruce Lee Rothschild proved that this problem has a solution, and it is a number that is greater than 6 (lower bound), and less than some N. The lower bound was subsequently raised to 13, and the upper bound was the name of a small number of graham. Graham's small number is less than the number in the Guinness Book of Records, but it's still an unimaginably huge number.

In general, Graham's task does not sound like something supernatural - a fifth grader can understand it. But to simple questions it is sometimes very difficult to get answers. If the solution is less than the Graham number we know, what is the answer? The Graham number, like some other large numbers, simply tells us that a certain problem basically has a solution, and this solution can be found. By optimizing the solution to the problem, we can move the Graham number closer to 1, and move it until we find a real solution.

As the number became a legend

So, Ronald Graham wrote a professional mathematical work on Ramsey theory, which attracted the attention of journalist Martin Gardner. It was Gardner who was able to get Graham's number in the Guinness Book of Records, after which the number attracted the attention of the general public.

The problem that Graham was trying to solve was, in fact, only one concrete example of the application of Ramsey’s theory. Further research in this theory gave mathematicians more numbers than even the Graham number. These numbers are not an exact solution to problems, but act as an upper bound.

Perhaps the best theorems in Ramsey theory can dramatically reduce upper bounds, which will lead to the disappearance of a huge number of super-large numbers. This, for example, happened with the Scuse number : in 1987 it was defined as 8.185 · 10 ³⁷⁰ , and after 30 years it turned out that it lies between 10 ¹⁹ and 1.3971672 · 10 ³¹⁶ .

What has Graham fascinated people with? Beauty and clarity.

To operate with giant numbers, Graham used fast-growing functions. Many of these functions are familiar to everyone — addition, multiplication, and exponentiation. Mathematicians have created new functions that scale much faster.

To write the number, Graham used Knut's switch notation , an extension of exponentiation. Just as exponentiation is repeated multiplication and is indicated by one arrow pointing up, two up arrows denote iterative exponentiation, three arrows denote repeated iterative exponentiation, etc.



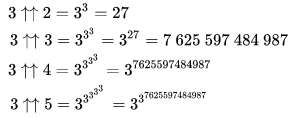
Or so:

3 ↑↑ 5 = 3 ↑ 3 ↑ 3 3 ↑ 3 = three to the power of three to the power of 7 625 597 484 987.

Mathematicians realized that, in dealing with large numbers, it is required each time to use a new operator, which should be more powerful than the previous one. ↑↑ is the next operator of ↑, just as ↑ is the next operator of multiplication, and just like multiplication is one operator of addition. Thus, increasing the number of consecutive arrows increases the ability to work with large numbers.

If you add another arrow, then the rate of formation of new numbers will increase significantly:
3 ↑↑↑ 3 gives us a tower of triples of 7 trillion high numbers.

Four arrows will give a number that will be very difficult to write down. Consider the following example from the remarkable Graham Number on Fingers article:



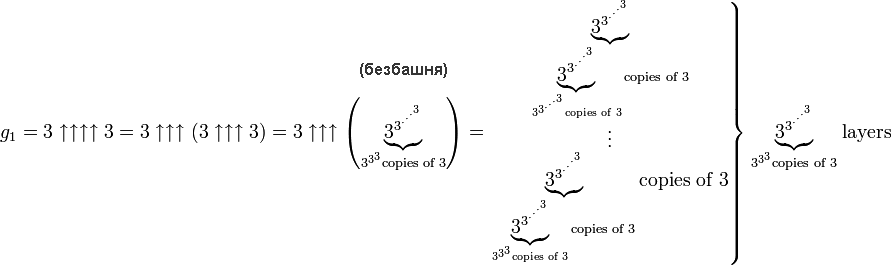
And here is the original illustration that Gardner used to explain Graham’s number:



The topmost level is 3 ↑↑↑↑ 3. The formula you saw above. Below it is a layer in which the number of arrows equals 3 ↑↑↑↑ 3. Next comes a layer in which the number of arrows equals the number of arrows in the previous layer. And so to the 64th layer.

The beauty of this expression is that if you want to exceed the Graham number and write “super-big number = Graeme number + 1”, then nothing will change in mathematical scales. It's like climbing to the top of Everest and jumping on it - Everest will still remain the highest mountain, to the top of which you can climb.

But somewhere in the solar system there is also Olympus , isn't it?

Bowers Notation: The Beginning of the Rabbit Hole

Further work with the Ramsey theory of mathematicians Joseph Kruskal and Harvey Friedman led to the number TREE (3), in which even the lowest limit of the solution is super-loud, not to mention the upper one.

If we can at least write the Graham number, then the TREE (3) number cannot be placed within the framework of Knut's notation. Judge for yourself:

TREE (3) = ...> A ^{A (187196)} (4), where even A ² (4) is greater than the number of atoms in the Universe, because A is the Akkerman function , which is defined recursively for non-negative integers m and n as follows:



Using the Ackermann function, it is very easy to write the Graham number ≈ A64 (4).

Mathematicians have calculated that TREE (3) has a theoretical limit, which can be written using massive notation , proposed in 2002 by Jonathan Bowers. In massive notation, there are five rules:

1. {a} = a and {a, b} = a ^b
2. {a, b, c, ..., n, 1} = {a, b, c, ..., n}
3. {a, 1, b, c, ..., n} = a
4. {a, b, 1, ..., 1, c, d ..., n} = {a, a, a, ..., {a, b - 1.1 ..., 1, c, d ..., n}, c - 1, d ..., n}
5. If rules 1-4 do not apply, then {a, b, c, d ..., n} = {a, {a, b - 1, c, d ..., n}, c - 1, d ..., n}

In the simplest case, a massive notation with an array of two elements is as follows: {10,100} = 10 ¹⁰⁰ or 10 ↑ 100.

The function grows incredibly fast. The array of three elements {10,100,2} in Knut's switch notation will be as follows: 10 ↑ ² 100.

The Bowers triple arrays are completely identical to the threefold chains of the Conway designation (another recording method — numbers connected by horizontal arrows (chains) grow faster than Knut's notation):

{3,3,3} = 3 → 3 → 3 = 3 ^ (3 ^ (3 ^ (3 ^ ... 7 625 597 484 987 times ... ^ 3) ^ 3) ^ 3)

The array of four elements (for example {10,100,1,2}) is already larger than the Graham number itself - thanks to the tricks invented by Bowers: on the fourth element it “optimizes” the formula, as we used to optimize multiplication and exponentiation, only now the mathematician is engaged in doubling brackets:

{3,3,1,2} = 3 {{1}} 3 = 3 {3 {3} 3} 3 = {3, 3, {3, 3, 3}}.

A more detailed analysis of this operation can be found in the article " Bird's Linear Array Notation ".



At the same time, “the largest number used in serious mathematical proof” is limited between {3.65,1,2} and {3.66,1.2}. We are now talking only about linear arrays, and in fact they can be hyperdimensional. In principle, the Bowers array of four elements is able to accommodate Conway’s entire notation , and hyperdimensional arrays (in the illustration above) are already becoming a mathematical hyper-game.

The beauty of mathematics is that we can work with data that we cannot even imagine. Any complex task can be simplified to incredibly simple values. Perhaps we will never find answers to some questions, but the methods used to solve them may be useful in other areas of knowledge. The very elaboration of these methods for building hierarchies in terms of the rate of growth of functions improves many branches of mathematics.

Bowers made a successful attempt to answer the question of how to expand the capabilities of the formal system with the help of a hierarchy of techniques. In fact, we are not recording the number itself in an allegorical way, but a way to ever come to this number, at least in theory.

Bowers notations have become an excellent opportunity to get to the understanding of the TREE function. Of course, we cannot determine the value of TREE (3), but using the iterative “improvement” of the notation, conducted by the English mathematician Chris Byrd, we found out that TREE (3)> {3,6,3 [1 [1–1,2 ] 2] 2}.

TREE (3)

TREE is a fast-growing function in graph theory developed by the mathematician Harvey Friedman.

Suppose we have a sequence of k-numbered trees T1, T2, ... with the following properties:

• each tree T _i has at most i vertices;
• no tree is incompatibly homeomorphic to any tree following it in a sequence.

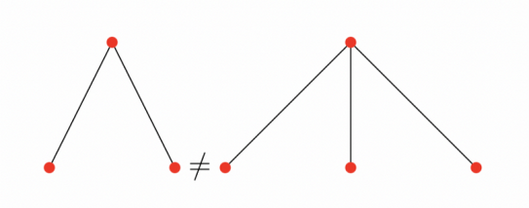
T _i <T _j , i.e. T _{i is not} embeddable in T _j

Such a sequence cannot be infinite. This theory was first proposed by Joseph Kruskal in 1960. Harvey Friedman expanded the theory by asking the question: given k, what is the maximum length of such a sequence of trees?

This maximum length is a function of k, called TREE (k).

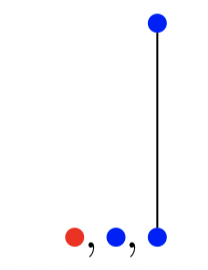
TREE (1) = 1. The first tree is a unique tree with one vertex labeled 1. This tree is obviously embeddable into any other tree, so we ended up with 1:



TREE (2) = 3. The first tree can only be a single one-vertex tree labeled 1 or 2. Denote it by 1 (red). Then no other trees can use label 1 - all vertices should be labeled with label 2 (blue). The second tree can be either a single single-vertex tree or a unique two-vertex tree:



Here we come to the most interesting: TREE (3) = ... - this is an incomprehensible great number. Probably the way to determine its scale will never be invented, since it is an order of magnitude higher than human capabilities. Let's see what the beginning of a number looks like:



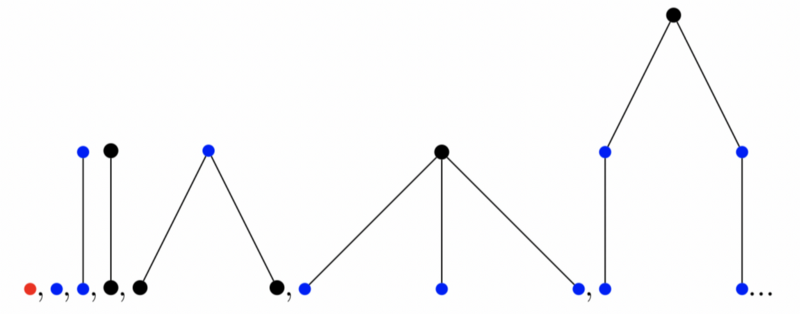
TREE (3) begins in this way and lasts for a VERY long time.

Abyss: SCG (n)

Mathematicians could not stop at TREE (3) and went on. No, not to TREE (4). The TREE (n) function is weaker compared to the Buchholz hydra and Subcubic Graph Numbers . Subcubic Graph Function - SCG (n) - gives the greatest result.

Here we need to make a small digression: from 1983 to 2004, mathematicians Neil Robertson and Paul D. Seymour in a 500-page study developed the theory that any inherited property of graphs is characterized by a finite number of forbidden subgraphs . The Robertson-Seymour theorem extends these results to arbitrary graph families that are closed in the minors. The theorem indicates that the set of toroidal graphs has a finite hindering set, but does not give any such set. The full set of forbidden minors for toroidal graphs remains unknown and contains at least 16 thousand graphs.

A simple subcubic graph is a finite simple graph in which each vertex has degree at most three. Suppose we have a sequence of simple subcubic graphs G1, G2, ... such that each graph G _i has at most i + k vertices (for some integer k) and embed homeomorphically in G _j .

The Robertson-Seymour theorem proves that subcubic graphs (simple or not) are fully justified by homeomorphic embeddability, implying that such a sequence cannot be infinite. Thus, for each value of k there is a sequence with a maximum length. The SSCG (k) function denotes this length for simple subcubic graphs. The function SCG (k) denotes this length for (general) subcubic graphs.

The SSCG sequence starts with SSCG (0) = 2, SSCG (1) = 5, but then it grows quickly. SSCG (2) = 3 × 23 × 295 - 8 ≈ 103.5775 × 1028.

SSCG (3) is not only larger than TREE (3), it is much larger than TREE (TREE (... TREE (3) ...)), where the total nesting depth of the formula is the TREE (3) level of the TREE function. There is no qualitative difference between the asymptotic growth rates of SSCG and SCG. It is clear that SCG (n) ≥ SSCG (n), but it can also be said that SSCG (4n + 3) ≥ SCG (n).

To infinity and beyond: BIG FOOT and other numbers

Mathematicians are still developing theories that can be used to create the “very-most” number. The “king” of the digital series often changes, but I want to finish today's review with a great number of BIG FOOT. Suppose it is larger than TREE (3) and SSCG (3) combined, but is no longer considered MOST big. However, the mechanics of its creation has not lost its relevance and is used to study the new greatest numbers.

Before moving on to the legendary snowman, let's get acquainted with Rayo's number theory. The Rayo number is a large number, named after the mathematician Agustín Rayo, who won the “large numbers duel” in 2007 with the following definition: “The smallest number that is greater than any finite number that can be defined by an expression in the first order language set theory using less than googol (10 ¹⁰⁰ ) characters ".

BIG FOOT is an analogue of Rayo's number - its definition is almost identical. BIG FOOT extends first-order set theory, using a unique area of ​​discourse, called oodleverse, using a language called first-orderoodletheory (FOOT), and generalizing n-order set theory of arbitrarily large n.

Let FOOT (n) denote the largest positive integer uniquely determined in the FOOT language by no more than n characters. BIG FOOT is defined as FOOT ¹⁰ (10 ¹⁰⁰ ), where FOOT ^a (n) is FOOT (n) (recursion).

BIG FOOT is thus equal to

FOOT (FOOT (FOOT (FOOT (FOOT (FOOT (FOOT (FOOT (FOOT (FOOT (10 ¹⁰⁰ ))))))))))

The search for a finite number continues. Will it ever be found?

Blaise Pascal described the existential horror as it encompasses him at the thought of the infinity of the world: “The eternal silence of this infinite space scares me.” The numbers give us the opportunity to establish the framework of understanding and the limits of what is permitted, to take control of the fear of the uroboros. They are our relic radiation, the ability to approach the metaphorical edge of the world. But just as in space one cannot fly to a place where the “End of the Universe” sign hangs, so in mathematics it is impossible to reach the last frontier. However, this is yet to be verified.

PS The author is not a professional mathematician and hopes that he did not make gross mistakes in the article. If you notice an inaccuracy - report. Also welcome comments that extend the material presented.

Sources:

• Howdoes Tree (3) grow to get so big? Need laymen explanation .
• TREE sequence
• SbiisSaibian's Large Number Site
• Subcubic Graph Numbers / restated