Binary tree numbering
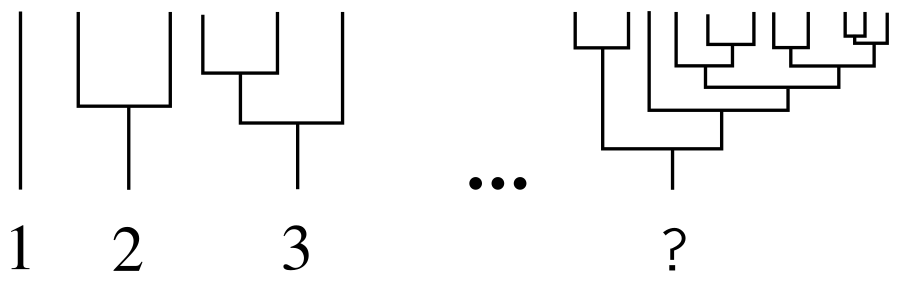
How to number all binary trees? As on the KDPV: the “tree” of one leaf will be the first, the tree of two sheets will be the second, the second tree with another branch coming from the root will be the third. And how to find the number of an arbitrary tree in such a scheme?
First of all, the motor scooter is not mine. The scheme described in the article was published by Caroline Colina and Giovanni Plazzotta (C. Colijn, G. Plazzotta) in Systematic Biology . But since most of the Habr hardly reads English biological journals, I decided that it was worth translating a piece from there.
Suppose that we already have a certain numbering scheme, and the numbering begins with a simple tree consisting of one sheet. We call a tree consisting of two subtrees with numbers k and j such that k > = j , (k, j) -tree . The set of ( k , j ) -trees will be ordered lexicographically: (1), (1, 1), (2, 1), (2, 2), (3, 1), (3, 2) ... there will be a place for the tree in that order That is, (1, 1) -tree is the same as tree number 2, (2, 1) -tree is the same as tree number 3, and so on. You can check: on KDPV the way it is.
')
To translate ( k, j ) -notation into numbers, you need to pay attention to the fact that this is essentially a sequence of all possible pairs of natural numbers. Since k > = j > = 1 by definition, there are exactly k ( k , j ) -pairs, from ( k , 1) to ( k , k ), for any k . Therefore, ( k , 1) -pair has the number (1 + 2 + 3 + ... + k -1) + 1, because it is preceded by (1 + 2 + 3 + ... + k -1) pairs. And, of course, the number of ( k , j ) -pairs is greater than the number of ( k , 1) -pairs of ( j -1). Substituting the formula for the sum of an arithmetic progression and reducing the extra units, we arrive at the following formula:
The extra unit is explained by the fact that the sequence does not begin with (1, 1) -, but with (1) -tree. Now the number of any arbitrary tree can be calculated in a recursive manner. The target tree is by definition a ( k , j ) -tree, where k and j are subtrees growing from its root. The k- tree, in turn, is ( k1 , k2 ) -tree, where k1 and k2 are its subtrees, and so on to the leaves, which are (1) -trees. For example:
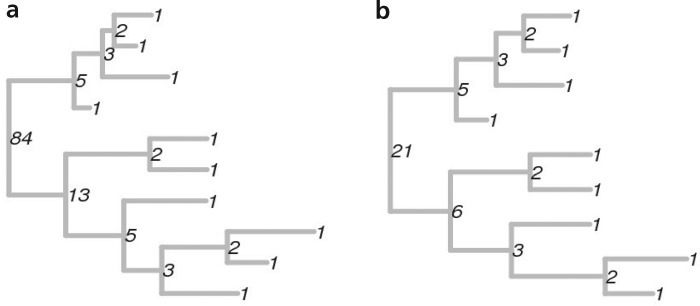
From this method of calculating the numbers and the practical meaning of the whole venture. Actually the numbers are a cool thing, but it's not very clear what to do with it further. Is that to admire how a huge number took up all your RAM and wants more (in practice: marking about a dozen trees with 500 leaves can not fit in 64 GB, even using gmpy2 ). They vary too much even with slight changes in the trees; the two trees in the picture above, for example, differ only in that in the right one sheet is missing at the very bottom. But each tree also corresponds to a vector of numbers of all its internal nodes. And on the vectors, it is already possible to determine the distance metric (for example, Euclidean) and use it for clustering tree topologies. In the original article, the trees were phylogenetic and managed to identify differences in the evolution of the influenza virus in the US and the tropics. In the tropics, the disease occurs throughout the year, so all intermediate forms are observed (mass ( k , 1) subtrees to the right). But in America, the flu is seasonal and mostly comes from abroad, so there are practically no such trees.
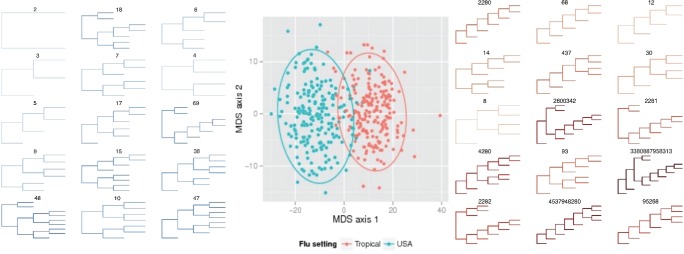
The original article still has a lot of interesting things: in particular, generalization for non-binary trees, various practically useful options for distance metrics, evidence that these are really metrics in the strict sense, the definition of mathematical operations on trees, and so on. If you suddenly want to play, then the author's code on R and my implementation on python are available on the githaba. Both, however, are designed for phylogenetic trees.

First of all, the motor scooter is not mine. The scheme described in the article was published by Caroline Colina and Giovanni Plazzotta (C. Colijn, G. Plazzotta) in Systematic Biology . But since most of the Habr hardly reads English biological journals, I decided that it was worth translating a piece from there.
Suppose that we already have a certain numbering scheme, and the numbering begins with a simple tree consisting of one sheet. We call a tree consisting of two subtrees with numbers k and j such that k > = j , (k, j) -tree . The set of ( k , j ) -trees will be ordered lexicographically: (1), (1, 1), (2, 1), (2, 2), (3, 1), (3, 2) ... there will be a place for the tree in that order That is, (1, 1) -tree is the same as tree number 2, (2, 1) -tree is the same as tree number 3, and so on. You can check: on KDPV the way it is.
')
To translate ( k, j ) -notation into numbers, you need to pay attention to the fact that this is essentially a sequence of all possible pairs of natural numbers. Since k > = j > = 1 by definition, there are exactly k ( k , j ) -pairs, from ( k , 1) to ( k , k ), for any k . Therefore, ( k , 1) -pair has the number (1 + 2 + 3 + ... + k -1) + 1, because it is preceded by (1 + 2 + 3 + ... + k -1) pairs. And, of course, the number of ( k , j ) -pairs is greater than the number of ( k , 1) -pairs of ( j -1). Substituting the formula for the sum of an arithmetic progression and reducing the extra units, we arrive at the following formula:
The extra unit is explained by the fact that the sequence does not begin with (1, 1) -, but with (1) -tree. Now the number of any arbitrary tree can be calculated in a recursive manner. The target tree is by definition a ( k , j ) -tree, where k and j are subtrees growing from its root. The k- tree, in turn, is ( k1 , k2 ) -tree, where k1 and k2 are its subtrees, and so on to the leaves, which are (1) -trees. For example:

From this method of calculating the numbers and the practical meaning of the whole venture. Actually the numbers are a cool thing, but it's not very clear what to do with it further. Is that to admire how a huge number took up all your RAM and wants more (in practice: marking about a dozen trees with 500 leaves can not fit in 64 GB, even using gmpy2 ). They vary too much even with slight changes in the trees; the two trees in the picture above, for example, differ only in that in the right one sheet is missing at the very bottom. But each tree also corresponds to a vector of numbers of all its internal nodes. And on the vectors, it is already possible to determine the distance metric (for example, Euclidean) and use it for clustering tree topologies. In the original article, the trees were phylogenetic and managed to identify differences in the evolution of the influenza virus in the US and the tropics. In the tropics, the disease occurs throughout the year, so all intermediate forms are observed (mass ( k , 1) subtrees to the right). But in America, the flu is seasonal and mostly comes from abroad, so there are practically no such trees.

The original article still has a lot of interesting things: in particular, generalization for non-binary trees, various practically useful options for distance metrics, evidence that these are really metrics in the strict sense, the definition of mathematical operations on trees, and so on. If you suddenly want to play, then the author's code on R and my implementation on python are available on the githaba. Both, however, are designed for phylogenetic trees.
Source: https://habr.com/ru/post/353338/
All Articles