Blockchain on Go. Part 5: Addresses
Content
In the previous article, we started the implementation of transactions, as well as familiarized ourselves with the principle of its operation: there are no accounts, personal data (for example, the name or series and passport number) are not required and are not stored anywhere in Bitcoin. But there must still be something that identifies you as the owner of the transaction outlets (i.e., the owner of the coins blocked at the exits). And this is what Bitcoin addresses are for. So far, we have used arbitrary strings as addresses, now it's time to implement real addresses, in the way they are implemented in Bitcoin.
In this part we will change a lot of code, so I see no reason to explain everything in detail. Visit this page to see all the changes compared to the previous article.
Here is an example of a Bitcoin address: 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa . This is the very first Bitcoin address that allegedly belongs to Satoshi Nakamoto. Bitcoin addresses are publicly available. If you want to send someone a coin, you need to know the address of the recipient. But addresses (despite the uniqueness) do not identify you as the owner of the "wallet". In fact, such addresses are a public key. In Bitcoin, your identity is a pair (or pairs) of private and public keys stored on your computer (or in some other place to which you have access). To create such keys, cryptographic algorithms are used that ensure that no one else can access your coins without physically accessing your keys. Let's look at what these algorithms are.
')
Algorithms of public-key cryptosystems use key pairs: public and private. Public keys can be reported to anyone. Private keys, on the contrary, should not be disclosed to anyone: no one except the owner should have access to them, since these are private keys that serve as the owner's identifier. Your face is your private keys (in the world of cryptocurrency, of course).
In fact, a bitcoin wallet is just a couple of such keys. When you install the wallet application or use the Bitcoin client to create a new address, a pair of keys is generated for you. The one who controls the private key controls all the coins that were sent to it.
Private and public keys are simply random sequences of bytes, so they cannot be printed on the screen and read by humans. This is why Bitcoin uses an algorithm to convert public keys into a readable string.
So now we know what identifies users in Bitcoin. But how does Bitcoin verify the owner of the exit transaction (and the coins that are stored there)?
In mathematics and cryptography, there is the concept of electronic digital signature - algorithms that guarantee:
Applying the algorithm of electronic digital signature to the data (i.e., by signing the data), a signature is obtained, which can later be verified. The data is signed using the private key, and the public key is required for verification.
To sign the data, we need the following:
The algorithm creates a signature that is stored in the inputs of the transaction. To verify the signature, you need the following:
In simple terms, the verification process can be described as follows: we need to make sure that the signature is obtained from this data using the private key that was used to generate the public key.
Each transaction entry in Bitcoin is signed by those who created this transaction. Each transaction in Bitcoin must be verified before placing it in a block. Verification means (besides other procedures):
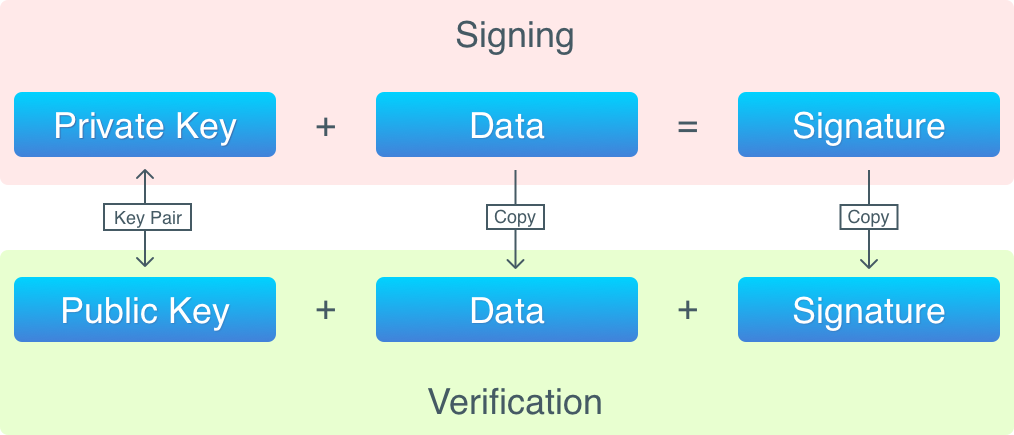
Schematically, the process of signing and verifying data is as follows:
Let's take a look at the full life cycle of a transaction:
As we already spoke with you, public and private keys are sequences of random bytes. We do not want to generate a private key belonging to someone else, so there is a need for a special algorithm for generating sequences.
Bitcoin uses elliptic curves to generate secret keys. Elliptic curves are a complex mathematical concept, which we will not explain in detail here (if interested, you can read about it here. WARNING : a lot of mathematics!). The curve used by Bitcoin can randomly select a number between 0 and 2²⁵⁶ (which is approximately 10⁷⁷, note, the atoms in the visible universe are somewhere between 10 and 10⁸²). Such a limit means that it is almost impossible to generate the same private key twice.
In addition, Bitcoin uses (and we will) the ECDSA algorithm to sign transactions.
Now let's go back to the above address 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa. We now know that this is a public-key representation of a public key. And if we decode it, it will look something like this (as a sequence of bytes written in hexadecimal):
Bitcoin uses the Base58 algorithm to convert public keys into human-readable format. The algorithm is very similar to the well-known Base64, but it uses a shorter alphabet: some letters have been removed from the alphabet to avoid homographic attacks . In this regard, the following symbols are missing in this alphabet: 0 (zero), O (capital letter “o”), I (capital letter “i”), l (lower case “L”) as well as the signs “+” and “/ ".
The process of getting an address from a public key looks like this:

Following this scheme, the key that we cited above is divided into three parts:
Well, now that we put the pieces together, it's time to write the code! I hope that now everything that was incomprehensible will become clear.
Let's start with the structure of the wallet wallet
A wallet is nothing but a pair of keys. We will also need the
Now, let's create an address generation function:
Let us step by step the conversion of the public key to the Base58 address:
As a result, you will get a real Bitcoin address , you can even check its balance on blockchain.info . But I am more than sure that nothing will be on the bill of this address. This is why choosing the right public key encryption algorithm is so important: given that the private keys are random numbers, the probability of generating the same number should be as small as possible. Ideally, it should not be repeated at all.
Please note that you do not need to connect to the Bitcoin node to get the address. The address generation algorithm uses a combination of algorithms that are already implemented in many standard libraries of popular programming languages.
Now we need to change the inputs and outputs to use the addresses:
Please note that we no longer use the
The
Now let's check that everything works correctly:
Fine! It's time to implement the signature transactions.
Transactions must be signed, as this is the only way to guarantee Bitcoin transaction reliability. If the signature is invalid, the transaction is considered invalid and, therefore, cannot be added to the chain.
We have everything to implement the signature to the transaction, except for one thing: the data to be signed. What part of the transaction should we sign? Or is it necessary to sign the deal as a whole? The choice of data to sign is very important. The point is that the data to be signed must contain information that identifies the data in a unique way. For example, it makes no sense to sign only output values, because such a signature will not take into account the sender and recipient.
Considering that transactions unblock previous outputs, redistribute their values and block new outputs, the following data should be signed:
In connection with this, in Bitcoin there is a signature not of a transaction, but of its processed copy with inputs that contain the
It all looks quite complicated, let's start writing code. And we begin with the
The method accepts a private key and an associative array of previous transactions. As mentioned above, to sign a transaction, we need to access the exits specified in the transaction inputs, so we need transactions that store these exits.
Let's take a closer look at this method:
Coinbase transactions are not signed, as there are no real exits
We sign the processed copy, not the entire transaction:
The copy will include all inputs and outputs, and
Then go through each entry in the copy:
At each input, the
The
We sign
Consider the verification function:
The method is quite simple. First, get a copy of the transaction, as in the past method:
Then we need a curve that is used to generate key pairs:
Then go through all the entrances and verify that they are signed:
This part is identical to that used in the Sign method, since during the test we need the same data that we signed
Here we unpack the values stored in
Now we create
Now we need a function to get previous transactions. Since this requires interaction with the entire chain, we will make it the
Now we need to sign and verify transactions. We will sign in the
Verification of the transaction occurs before it is added to the block:
That's all! Let's check again:
We didn't even break anything, amazing!
Let's comment out the
We have implemented almost all the key features of Bitcoin and this is amazing. And in the next part, we will finally complete the implementation of transactions.
- Blockchain on Go. Part 1: Prototype
- Blockchain on Go. Part 2: Proof-of-Work
- Blockchain on Go. Part 3: Permanent Memory and Command Line Interface
- Blockchain on Go. Part 4: Transactions, Part 1
- Blockchain on Go. Part 5: Addresses
- Blockchain on Go. Part 6: Transactions, Part 2
- Blockchain on Go. Part 7: Network
Introduction
In the previous article, we started the implementation of transactions, as well as familiarized ourselves with the principle of its operation: there are no accounts, personal data (for example, the name or series and passport number) are not required and are not stored anywhere in Bitcoin. But there must still be something that identifies you as the owner of the transaction outlets (i.e., the owner of the coins blocked at the exits). And this is what Bitcoin addresses are for. So far, we have used arbitrary strings as addresses, now it's time to implement real addresses, in the way they are implemented in Bitcoin.
In this part we will change a lot of code, so I see no reason to explain everything in detail. Visit this page to see all the changes compared to the previous article.
Bitcoin address
Here is an example of a Bitcoin address: 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa . This is the very first Bitcoin address that allegedly belongs to Satoshi Nakamoto. Bitcoin addresses are publicly available. If you want to send someone a coin, you need to know the address of the recipient. But addresses (despite the uniqueness) do not identify you as the owner of the "wallet". In fact, such addresses are a public key. In Bitcoin, your identity is a pair (or pairs) of private and public keys stored on your computer (or in some other place to which you have access). To create such keys, cryptographic algorithms are used that ensure that no one else can access your coins without physically accessing your keys. Let's look at what these algorithms are.
')
Public key cryptosystem
Algorithms of public-key cryptosystems use key pairs: public and private. Public keys can be reported to anyone. Private keys, on the contrary, should not be disclosed to anyone: no one except the owner should have access to them, since these are private keys that serve as the owner's identifier. Your face is your private keys (in the world of cryptocurrency, of course).
In fact, a bitcoin wallet is just a couple of such keys. When you install the wallet application or use the Bitcoin client to create a new address, a pair of keys is generated for you. The one who controls the private key controls all the coins that were sent to it.
Private and public keys are simply random sequences of bytes, so they cannot be printed on the screen and read by humans. This is why Bitcoin uses an algorithm to convert public keys into a readable string.
If you have ever used a Bitcoin wallet as an application, it is likely that a mnemonic phrase was created for you. Such phrases are used instead of private keys and can be used to generate them. This mechanism is implemented in BIP-039 .
So now we know what identifies users in Bitcoin. But how does Bitcoin verify the owner of the exit transaction (and the coins that are stored there)?
Electronic digital signature
In mathematics and cryptography, there is the concept of electronic digital signature - algorithms that guarantee:
- that the data has not been changed during transmission from the sender to the recipient
- that the data was created by a specific sender;
- that the sender cannot deny that he sent the data.
Applying the algorithm of electronic digital signature to the data (i.e., by signing the data), a signature is obtained, which can later be verified. The data is signed using the private key, and the public key is required for verification.
To sign the data, we need the following:
- signature data;
- private key
The algorithm creates a signature that is stored in the inputs of the transaction. To verify the signature, you need the following:
- data that has been signed;
- signature;
- public key.
In simple terms, the verification process can be described as follows: we need to make sure that the signature is obtained from this data using the private key that was used to generate the public key.
Digital signatures are not encrypted, and data cannot be obtained from it. This is similar to hashing: you convert data using an algorithm and get their unique representation. The difference between the hash and the signature is the key pair that allows you to verify the latter.
But such key pairs can also be used to encrypt data: the private key is used for encryption, and the public key is used for decryption. However, Bitcoin does not use encryption algorithms.
Each transaction entry in Bitcoin is signed by those who created this transaction. Each transaction in Bitcoin must be verified before placing it in a block. Verification means (besides other procedures):
- Verify that the inputs have sufficient rights to use the outputs from previous transactions.
- Verifying the signature of a transaction.
Schematically, the process of signing and verifying data is as follows:

Let's take a look at the full life cycle of a transaction:
- At the very beginning there is a genesis block with a coinbase transaction. There are no real entries in coinbase transactions, so no signature is required. The withdrawal of the transaction contains the hashed public key (
RIPEMD16(SHA256(PubKey))algorithms are usedRIPEMD16(SHA256(PubKey))). - When someone sends coins, a transaction is created. Transaction entries will refer to exits from previous transactions. Each entry will store the public key (not hashed) and the signature of the entire transaction.
- Other nodes on the Bitcoin network that receive the transaction will also check it. Among other things, here is the comparison of the public key hash at the input of the transaction with the hash of the corresponding output (this ensures that the sender spends only the coins belonging to him); the signature is correct (this ensures that the transaction is created by the real owner of the coins).
- When the node is ready for mining a new block, it will put the transaction in the block and start mining it.
- When the block is mined, every other node in the network receives a message that the block has been mined and adds it to the chain.
- After the block is added to the chain, the transaction is completed, now its outputs can be referenced in new transactions.
Elliptical cryptography
As we already spoke with you, public and private keys are sequences of random bytes. We do not want to generate a private key belonging to someone else, so there is a need for a special algorithm for generating sequences.
Bitcoin uses elliptic curves to generate secret keys. Elliptic curves are a complex mathematical concept, which we will not explain in detail here (if interested, you can read about it here. WARNING : a lot of mathematics!). The curve used by Bitcoin can randomly select a number between 0 and 2²⁵⁶ (which is approximately 10⁷⁷, note, the atoms in the visible universe are somewhere between 10 and 10⁸²). Such a limit means that it is almost impossible to generate the same private key twice.
In addition, Bitcoin uses (and we will) the ECDSA algorithm to sign transactions.
Base58
Now let's go back to the above address 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa. We now know that this is a public-key representation of a public key. And if we decode it, it will look something like this (as a sequence of bytes written in hexadecimal):
0062E907B15CBF27D5425399EBF6F0FB50EBB88F18C29B7D93 Bitcoin uses the Base58 algorithm to convert public keys into human-readable format. The algorithm is very similar to the well-known Base64, but it uses a shorter alphabet: some letters have been removed from the alphabet to avoid homographic attacks . In this regard, the following symbols are missing in this alphabet: 0 (zero), O (capital letter “o”), I (capital letter “i”), l (lower case “L”) as well as the signs “+” and “/ ".
The process of getting an address from a public key looks like this:

Following this scheme, the key that we cited above is divided into three parts:
Version 00 Public key hash 62E907B15CBF27D5425399EBF6F0FB50EBB88F18 Checksum C29B7D93 Well, now that we put the pieces together, it's time to write the code! I hope that now everything that was incomprehensible will become clear.
Implementation of addresses
Let's start with the structure of the wallet wallet
type Wallet struct { PrivateKey ecdsa.PrivateKey PublicKey []byte } type Wallets struct { Wallets map[string]*Wallet } func NewWallet() *Wallet { private, public := newKeyPair() wallet := Wallet{private, public} return &wallet } func newKeyPair() (ecdsa.PrivateKey, []byte) { curve := elliptic.P256() private, err := ecdsa.GenerateKey(curve, rand.Reader) pubKey := append(private.PublicKey.X.Bytes(), private.PublicKey.Y.Bytes()...) return *private, pubKey } A wallet is nothing but a pair of keys. We will also need the
Wallets type to store a collection of wallets, save them to a file and unload them from it. A new key pair is created in the Wallet constructor. The newKeyPair function newKeyPair simple, here we use ECDSA. The private key is then created using a curve, and the public key is generated using the private key. One note: in elliptic curve based algorithms, public keys are points on a curve. Thus, a public key is a combination of X, Y coordinates. In Bitcoin, these coordinates are combined to form a public key.Now, let's create an address generation function:
func (w Wallet) GetAddress() []byte { pubKeyHash := HashPubKey(w.PublicKey) versionedPayload := append([]byte{version}, pubKeyHash...) checksum := checksum(versionedPayload) fullPayload := append(versionedPayload, checksum...) address := Base58Encode(fullPayload) return address } func HashPubKey(pubKey []byte) []byte { publicSHA256 := sha256.Sum256(pubKey) RIPEMD160Hasher := ripemd160.New() _, err := RIPEMD160Hasher.Write(publicSHA256[:]) publicRIPEMD160 := RIPEMD160Hasher.Sum(nil) return publicRIPEMD160 } func checksum(payload []byte) []byte { firstSHA := sha256.Sum256(payload) secondSHA := sha256.Sum256(firstSHA[:]) return secondSHA[:addressChecksumLen] } Let us step by step the conversion of the public key to the Base58 address:
- Take the public key and write it twice using the
RIPEMD160 (SHA256 (PubKey))hashing algorithms. - Prepare a version.
- Calculate the checksum by hashing the result from step 2 and
SHA256 (SHA256 (payload)). The checksum is the first four bytes of the received hash. - Add a checksum to the combination
version+PubKeyHash. - Encrypt the
version+PubKeyHash+checksumcombination using Base58.
As a result, you will get a real Bitcoin address , you can even check its balance on blockchain.info . But I am more than sure that nothing will be on the bill of this address. This is why choosing the right public key encryption algorithm is so important: given that the private keys are random numbers, the probability of generating the same number should be as small as possible. Ideally, it should not be repeated at all.
Please note that you do not need to connect to the Bitcoin node to get the address. The address generation algorithm uses a combination of algorithms that are already implemented in many standard libraries of popular programming languages.
Now we need to change the inputs and outputs to use the addresses:
type TXInput struct { Txid []byte Vout int Signature []byte PubKey []byte } func (in *TXInput) UsesKey(pubKeyHash []byte) bool { lockingHash := HashPubKey(in.PubKey) return bytes.Compare(lockingHash, pubKeyHash) == 0 } type TXOutput struct { Value int PubKeyHash []byte } func (out *TXOutput) Lock(address []byte) { pubKeyHash := Base58Decode(address) pubKeyHash = pubKeyHash[1 : len(pubKeyHash)-4] out.PubKeyHash = pubKeyHash } func (out *TXOutput) IsLockedWithKey(pubKeyHash []byte) bool { return bytes.Compare(out.PubKeyHash, pubKeyHash) == 0 } Please note that we no longer use the
ScriptPubKey and ScriptSig , instead ScriptSig is divided into Signature and PubKey , and ScriptPubKey renamed to PubKeyHash . We will implement the same functions of blocking / unblocking outputs and logic of input signatures, as in Bitcoin, but we will implement this using methods.The
UsesKey method verifies that the input uses a specific key to unlock the output. Please note that the inputs store unshaded public keys, and the function accepts hashed. IsLockedWithKey checks if the hash key of the public key was used to block the output. This is an optional feature for UsesKey , and both are used in FindUnspentTransactions to build connections between transactions.Lock simply blocks the exit. When we send coins to someone, we only know the address, so the function takes the address as the only argument. Then the address is decoded, and the public key hash key is extracted from it and stored in the PubKeyHash field.Now let's check that everything works correctly:
$ blockchain_go createwallet Your new address: 13Uu7B1vDP4ViXqHFsWtbraM3EfQ3UkWXt $ blockchain_go createwallet Your new address: 15pUhCbtrGh3JUx5iHnXjfpyHyTgawvG5h $ blockchain_go createwallet Your new address: 1Lhqun1E9zZZhodiTqxfPQBcwr1CVDV2sy $ blockchain_go createblockchain -address 13Uu7B1vDP4ViXqHFsWtbraM3EfQ3UkWXt 0000005420fbfdafa00c093f56e033903ba43599fa7cd9df40458e373eee724d Done! $ blockchain_go getbalance -address 13Uu7B1vDP4ViXqHFsWtbraM3EfQ3UkWXt Balance of '13Uu7B1vDP4ViXqHFsWtbraM3EfQ3UkWXt': 10 $ blockchain_go send -from 15pUhCbtrGh3JUx5iHnXjfpyHyTgawvG5h -to 13Uu7B1vDP4ViXqHFsWtbraM3EfQ3UkWXt -amount 5 2017/09/12 13:08:56 ERROR: Not enough funds $ blockchain_go send -from 13Uu7B1vDP4ViXqHFsWtbraM3EfQ3UkWXt -to 15pUhCbtrGh3JUx5iHnXjfpyHyTgawvG5h -amount 6 00000019afa909094193f64ca06e9039849709f5948fbac56cae7b1b8f0ff162 Success! $ blockchain_go getbalance -address 13Uu7B1vDP4ViXqHFsWtbraM3EfQ3UkWXt Balance of '13Uu7B1vDP4ViXqHFsWtbraM3EfQ3UkWXt': 4 $ blockchain_go getbalance -address 15pUhCbtrGh3JUx5iHnXjfpyHyTgawvG5h Balance of '15pUhCbtrGh3JUx5iHnXjfpyHyTgawvG5h': 6 $ blockchain_go getbalance -address 1Lhqun1E9zZZhodiTqxfPQBcwr1CVDV2sy Balance of '1Lhqun1E9zZZhodiTqxfPQBcwr1CVDV2sy': 0 Fine! It's time to implement the signature transactions.
Implementation of signatures
Transactions must be signed, as this is the only way to guarantee Bitcoin transaction reliability. If the signature is invalid, the transaction is considered invalid and, therefore, cannot be added to the chain.
We have everything to implement the signature to the transaction, except for one thing: the data to be signed. What part of the transaction should we sign? Or is it necessary to sign the deal as a whole? The choice of data to sign is very important. The point is that the data to be signed must contain information that identifies the data in a unique way. For example, it makes no sense to sign only output values, because such a signature will not take into account the sender and recipient.
Considering that transactions unblock previous outputs, redistribute their values and block new outputs, the following data should be signed:
- Public key hashes stored in unlocked exits. This identifies the "sender" of the transaction.
- Public key hashes stored in new, locked, exits. This identifies the "recipient" of the transaction.
- Values of new outputs.
In Bitcoin, the lock / unlock logic is stored in scripts that are stored in theScriptSigandScriptPubKeyinput and output fields, respectively. Because Bitcoin allows for different types of such scripts, it signs the entire contents of theScriptPubKey.
In connection with this, in Bitcoin there is a signature not of a transaction, but of its processed copy with inputs that contain the
ScriptPubKey specified outputThis is a detailed process for handling a copy of a transaction. Most likely, it is outdated, but I could not find a more reliable source of information.
It all looks quite complicated, let's start writing code. And we begin with the
Sign method: func (tx *Transaction) Sign(privKey ecdsa.PrivateKey, prevTXs map[string]Transaction) { if tx.IsCoinbase() { return } txCopy := tx.TrimmedCopy() for inID, vin := range txCopy.Vin { prevTx := prevTXs[hex.EncodeToString(vin.Txid)] txCopy.Vin[inID].Signature = nil txCopy.Vin[inID].PubKey = prevTx.Vout[vin.Vout].PubKeyHash txCopy.ID = txCopy.Hash() txCopy.Vin[inID].PubKey = nil r, s, err := ecdsa.Sign(rand.Reader, &privKey, txCopy.ID) signature := append(r.Bytes(), s.Bytes()...) tx.Vin[inID].Signature = signature } } The method accepts a private key and an associative array of previous transactions. As mentioned above, to sign a transaction, we need to access the exits specified in the transaction inputs, so we need transactions that store these exits.
Let's take a closer look at this method:
if tx.IsCoinbase() { return } Coinbase transactions are not signed, as there are no real exits
txCopy := tx.TrimmedCopy() We sign the processed copy, not the entire transaction:
func (tx *Transaction) TrimmedCopy() Transaction { var inputs []TXInput var outputs []TXOutput for _, vin := range tx.Vin { inputs = append(inputs, TXInput{vin.Txid, vin.Vout, nil, nil}) } for _, vout := range tx.Vout { outputs = append(outputs, TXOutput{vout.Value, vout.PubKeyHash}) } txCopy := Transaction{tx.ID, inputs, outputs} return txCopy } The copy will include all inputs and outputs, and
TXInput.Signature and TXInput.PubKey will be equal to nil.Then go through each entry in the copy:
for inID, vin := range txCopy.Vin { prevTx := prevTXs[hex.EncodeToString(vin.Txid)] txCopy.Vin[inID].Signature = nil txCopy.Vin[inID].PubKey = prevTx.Vout[vin.Vout].PubKeyHash At each input, the
Signature set to nil (just a double check), and PubKey assigned a link to the exit to PubKeyHash . At the moment, all transactions, except for the current one, are “empty”, that is, the signature and PubKey are zero. Thus, the inputs are signed separately , although this is not necessary for our application, but Bitcoin allows transactions to contain inputs that refer to different addresses. txCopy.ID = txCopy.Hash() txCopy.Vin[inID].PubKey = nil The
Hash method serializes a transaction and hashes it using the SHA-256 algorithm. The result is data ready for signature. After receiving the hash, we have to reset the PubKey field PubKey that there is no impact on our further iterations. r, s, err := ecdsa.Sign(rand.Reader, &privKey, txCopy.ID) signature := append(r.Bytes(), s.Bytes()...) tx.Vin[inID].Signature = signature We sign
txCopy.ID with privKey . The ECDSA signature is a pair of numbers that we combine and store in the Signature input field.Consider the verification function:
func (tx *Transaction) Verify(prevTXs map[string]Transaction) bool { txCopy := tx.TrimmedCopy() curve := elliptic.P256() for inID, vin := range tx.Vin { prevTx := prevTXs[hex.EncodeToString(vin.Txid)] txCopy.Vin[inID].Signature = nil txCopy.Vin[inID].PubKey = prevTx.Vout[vin.Vout].PubKeyHash txCopy.ID = txCopy.Hash() txCopy.Vin[inID].PubKey = nil r := big.Int{} s := big.Int{} sigLen := len(vin.Signature) r.SetBytes(vin.Signature[:(sigLen / 2)]) s.SetBytes(vin.Signature[(sigLen / 2):]) x := big.Int{} y := big.Int{} keyLen := len(vin.PubKey) x.SetBytes(vin.PubKey[:(keyLen / 2)]) y.SetBytes(vin.PubKey[(keyLen / 2):]) rawPubKey := ecdsa.PublicKey{curve, &x, &y} if ecdsa.Verify(&rawPubKey, txCopy.ID, &r, &s) == false { return false } } return true } The method is quite simple. First, get a copy of the transaction, as in the past method:
txCopy := tx.TrimmedCopy() Then we need a curve that is used to generate key pairs:
curve := elliptic.P256() Then go through all the entrances and verify that they are signed:
for inID, vin := range tx.Vin { prevTx := prevTXs[hex.EncodeToString(vin.Txid)] txCopy.Vin[inID].Signature = nil txCopy.Vin[inID].PubKey = prevTx.Vout[vin.Vout].PubKeyHash txCopy.ID = txCopy.Hash() txCopy.Vin[inID].PubKey = nil This part is identical to that used in the Sign method, since during the test we need the same data that we signed
r := big.Int{} s := big.Int{} sigLen := len(vin.Signature) r.SetBytes(vin.Signature[:(sigLen / 2)]) s.SetBytes(vin.Signature[(sigLen / 2):]) x := big.Int{} y := big.Int{} keyLen := len(vin.PubKey) x.SetBytes(vin.PubKey[:(keyLen / 2)]) y.SetBytes(vin.PubKey[(keyLen / 2):]) Here we unpack the values stored in
TXInput.Signature and TXInput.PubKey , since the signature is a pair of numbers, and the public key is a pair of coordinates. We have concatenated them before for storage, and now we need to unpack them for use in the crypto/ecdsa . rawPubKey := ecdsa.PublicKey{curve, &x, &y} if ecdsa.Verify(&rawPubKey, txCopy.ID, &r, &s) == false { return false } } return true Now we create
ecdsa.PublicKey using the public key, which we take from the input, and execute ecdsa.Verify , passing the signature, from the input. If all entries are verified, we return true; if at least one entry fails validation, return false.Now we need a function to get previous transactions. Since this requires interaction with the entire chain, we will make it the
Blockchain method: func (bc *Blockchain) FindTransaction(ID []byte) (Transaction, error) { bci := bc.Iterator() for { block := bci.Next() for _, tx := range block.Transactions { if bytes.Compare(tx.ID, ID) == 0 { return *tx, nil } } if len(block.PrevBlockHash) == 0 { break } } return Transaction{}, errors.New("Transaction is not found") } func (bc *Blockchain) SignTransaction(tx *Transaction, privKey ecdsa.PrivateKey) { prevTXs := make(map[string]Transaction) for _, vin := range tx.Vin { prevTX, err := bc.FindTransaction(vin.Txid) prevTXs[hex.EncodeToString(prevTX.ID)] = prevTX } tx.Sign(privKey, prevTXs) } func (bc *Blockchain) VerifyTransaction(tx *Transaction) bool { prevTXs := make(map[string]Transaction) for _, vin := range tx.Vin { prevTX, err := bc.FindTransaction(vin.Txid) prevTXs[hex.EncodeToString(prevTX.ID)] = prevTX } return tx.Verify(prevTXs) } FindTransaction finds a transaction by identifier (this requires iteration over all blocks in the chain); SignTransaction takes one transaction, finds the transactions to which it refers, and signs it; VerifyTransaction simply verifies the transaction.Now we need to sign and verify transactions. We will sign in the
NewUTXOTransaction method: func NewUTXOTransaction(from, to string, amount int, bc *Blockchain) *Transaction { ... tx := Transaction{nil, inputs, outputs} tx.ID = tx.Hash() bc.SignTransaction(&tx, wallet.PrivateKey) return &tx } Verification of the transaction occurs before it is added to the block:
func (bc *Blockchain) MineBlock(transactions []*Transaction) { var lastHash []byte for _, tx := range transactions { if bc.VerifyTransaction(tx) != true { log.Panic("ERROR: Invalid transaction") } } ... } That's all! Let's check again:
$ blockchain_go createwallet Your new address: 1AmVdDvvQ977oVCpUqz7zAPUEiXKrX5avR $ blockchain_go createwallet Your new address: 1NE86r4Esjf53EL7fR86CsfTZpNN42Sfab $ blockchain_go createblockchain -address 1AmVdDvvQ977oVCpUqz7zAPUEiXKrX5avR 000000122348da06c19e5c513710340f4c307d884385da948a205655c6a9d008 Done! $ blockchain_go send -from 1AmVdDvvQ977oVCpUqz7zAPUEiXKrX5avR -to 1NE86r4Esjf53EL7fR86CsfTZpNN42Sfab -amount 6 0000000f3dbb0ab6d56c4e4b9f7479afe8d5a5dad4d2a8823345a1a16cf3347b Success! $ blockchain_go getbalance -address 1AmVdDvvQ977oVCpUqz7zAPUEiXKrX5avR Balance of '1AmVdDvvQ977oVCpUqz7zAPUEiXKrX5avR': 4 $ blockchain_go getbalance -address 1NE86r4Esjf53EL7fR86CsfTZpNN42Sfab Balance of '1NE86r4Esjf53EL7fR86CsfTZpNN42Sfab': 6 We didn't even break anything, amazing!
Let's comment out the
bc.SignTransaction (& tx, wallet.PrivateKey) in NewUTXOTransaction , to ensure that unsigned transactions cannot be minted: func NewUTXOTransaction(from, to string, amount int, bc *Blockchain) *Transaction { ... tx := Transaction{nil, inputs, outputs} tx.ID = tx.Hash() // bc.SignTransaction(&tx, wallet.PrivateKey) return &tx } $ go install $ blockchain_go send -from 1AmVdDvvQ977oVCpUqz7zAPUEiXKrX5avR -to 1NE86r4Esjf53EL7fR86CsfTZpNN42Sfab -amount 1 2017/09/12 16:28:15 ERROR: Invalid transaction Conclusion
We have implemented almost all the key features of Bitcoin and this is amazing. And in the next part, we will finally complete the implementation of transactions.
Links
Source: https://habr.com/ru/post/351834/
All Articles