Triton vs Kao's Toy Project. We continue a good tradition

This article will discuss SMT solvers. It so happened that a good tradition appeared in the research materials devoted to this topic. Already several times, different researchers have chosen the same example as the experimental algorithm for SMT solvers - the cracks that were invented once by a person with the nickname kao . Well, let's continue this tradition and try to use another symbolic tool to solve this cracks - Triton .

A couple of words about SMT-solvers

The task of satisfiability of formulas in theories (SMT) is the task of satisfiability for logical formulas taking into account the theories underlying them. Examples of such theories for SMT formulas are: theories of integers and real numbers, the theory of lists, arrays, bit vectors, etc. - wikipedia

The SMT task is an extension of the SAT task (the Boolean satisfiability problem or the Propositional Satisfiability Problem, in the English-language literature it is called the SATISFIABILITY or SAT, in Russian literature it is sometimes called EX).

Another quote from Wikipedia:

An instance of the SAT task is a boolean formula consisting only of variable names, parentheses, and AND, OR, and HE operations. The problem is the following: is it possible to assign all the variables found in the formula the values ​​"false" and "true" so that the formula becomes true. - wikipedia

Since SMT solvers work with different theories, it becomes possible to use them for algorithms in traditional processor architectures. Thus, SMT solvers solve two problems:

• to answer the question whether the data is possible output values ​​of the algorithm with the given input values;
• to determine at what input values ​​the result of the algorithm will be the given output values.

SMT solvers have applied applications in various fields of science and technology. There are separate tools for solving SMT formulas, for example, Z3 , miniSAT , CVC4 , etc., and for representing algorithms in machine language in the syntax of an SMT formula , for example, BAP , radare2, or angr . The tools are constantly being improved, the API is becoming more powerful, and now just a few clicks are enough to apply the entire SMT mathematical apparatus in reverse engineering tasks.

Note also that there are several types of symbolic execution. Static symbolic execution (SSE, Static symbolic execution) is based only on symbolic variables and uses only symbolic formulas. Dynamic symbolic execution (DSE, Dynamic symbolic execution), also called concolic execution, uses symbolic computations along with specific values ​​of numerical variables during program execution. In this paper we will use only static symbolic execution.

Quack history Kao's Toy Project

Cracks Kao's Toy Project is extremely simple. In one window, it displays some hexadecimal sequence and offers to enter a key that is valid for the sequence.

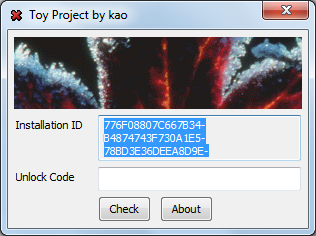
His story can be presented as the following chronicle:

03/04/2012 - Kao's Toy Project and Algebraic Cryptanalysis - dcoder, andrewl - Algebraic Cryptanalysis, SAT

The first work devoted to this quack, appeared in 2012. In it, a person with the nickname dcoder published a solution using algebraic cryptanalysis, and the co-author of this work andrewl successfully applied the SAT solver.

03/06/2012 - Rolf Rolles - z3, Self-Writing Converter

Then the famous researcher Rolf Rolles first applied the SMT solver to the solution. First, he manually compiled a formula in Z3, and then presented in OCaml a tool for automatically generating a formula from an intermediate representation of machine code. The intermediate language he used was developed by himself.

I used an BitBlaze and BAP, but I wrote my own IR translator rather than using VEX. My implementation is written with the open-source framework. - openrce.org

11.2013 - SMT Solvers for Software Security - Georgy Nosenko - BAP, z3

Then came the work of my colleague Georgy Nosenko, where the BAP framework and the same solver Z3 were already used to generate the formula.

03.2015 - Automated algebraic cryptanalysis with OpenREIL and Z3 - Cr4sh - OpenREIL, z3

Dmitry Oleksyuk, also known as Cr4sh, in his study used the conversion into the intermediate language OpenREIL with the subsequent generation of the formula in Z3.

04.2016 - Extreme Coders Blog - Solr

And finally, another work appeared in 2016, and it describes the solution using the framework angr. Angr uses the intermediate language VEX and the claripy library for symbolic performance.

At the SMT arena, another player has now appeared - Triton, and we will use it in this paper to solve the famous quacks.

Triton

Triton was created by Quarkslab , which created many interesting tools for reverse engineering.

First, a little about how Triton works. In the course of his work, he performs the following actions:

1. parses the trace of the binary code execution and generates an abstract syntax tree of the code taking into account all the side effects of machine instructions;
2. bypasses the abstract syntax tree and generates an SMT formula in SMT-LIB format;
3. Solves a formula with the solver z3.

When building an abstract syntax tree, Triton does not use an intermediate representation of machine code (unlike bap or angr), and currently supports only work with x86 and x86-64 architectures.

Triton can work in one of two modes. In the first one, online mode, the execution trace is recorded using a special tracer, which is part of Triton and uses the DBI framework pin . In the second - offline mode - the track is recorded by external means. The route must contain a sequence of instructions and their opcodes. In the second case, it is already necessary to independently create the initial context, that is, to determine the values ​​of the registers and the memory used.

The API that Triton provides is very rich and ... very unstable. Since the advent of the API has changed four times already, of course, not retaining backward compatibility. Because of this, the code of old tools using Triton must be rewritten to run on new versions. The nice thing is that the API has binding for Python. There are several examples in the repository that demonstrate the use of API in C ++ and Python, thanks to which it is quite easy to deal with it.

So let's get down to the solution.

Decision

First we need to find the algorithm by which the entered key is checked. Skimming through the code, we see that the generated sequence is actually eight 32-bit integers, and lies in memory sequentially in the little-endian representation, while the window is shown as big-endian. We learn that the key has the format XXXXXXXX-XXXXXXXX, where X is a hexadecimal digit. If the key is entered in this format, the verification procedure is called. So it looks like in the IDA Pro disassembler.

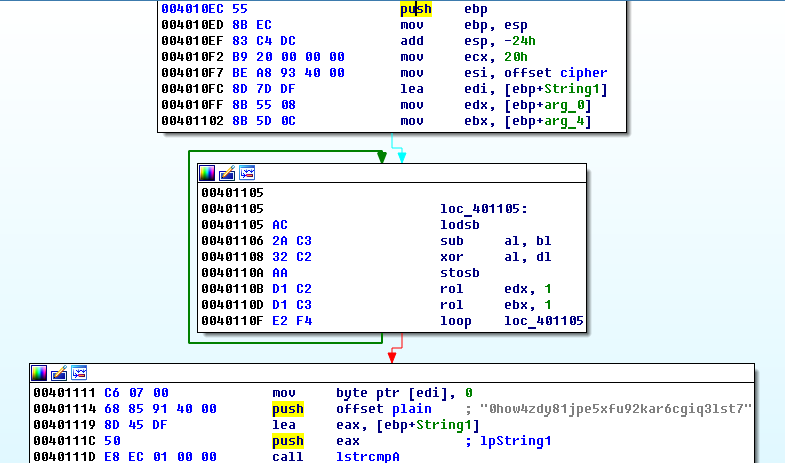
The verification procedure first initializes the input data: cipher is a 32-byte source sequence in little-endian view, String1 is the buffer for the output sequence after conversion, in the edx and ebx registers there are two key halves, represented as 32-bit integers. Next comes the conversion algorithm itself - 32 cycles with xor and rol operations - and then the resulting string from the String1 buffer is compared with the string “0how4zdy81jpe5xfu92kar6cgiq3lst7”. If they are identical, the key is considered valid.

Thus, the following problem is formed for the SMT solver: to determine on which input values ​​of the edx and ebx registers a given hexadecimal sequence after the execution of the algorithm is converted into the string “0how4zdy81jpe5xfu92kar6cgiq3lst7”.

Since cracks are written for Windows, the Triton tracer is not suitable, because it is supplied only compiled for Linux. You can, of course, try to compile it yourself for Windows, but these are still adventures. Therefore, we will use offline mode and Triton's Binding for Python.

First we introduce the necessary constants:

ADDR_CIPHER = 0x4093A8 ADDR_TEXT = 0x409185 ADDR_EBP = 0x18f980 TEXT = "0how4zdy81jpe5xfu92kar6cgiq3lst7" cipher = None 

and perform the initial initialization:

 ctx = TritonContext() ctx.setArchitecture(ARCH.X86) ctx.setConcreteRegisterValue(ctx.registers.ebp, ADDR_EBP) ctx.setConcreteRegisterValue(ctx.registers.esp, 0x18f95b) ctx.setConcreteRegisterValue(ctx.registers.eip, 0x4010ec) ctx.setConcreteMemoryAreaValue(ADDR_CIPHER, cipher) ctx.setConcreteMemoryAreaValue(ADDR_TEXT, list(map(ord, TEXT))) edx = ctx.convertRegisterToSymbolicVariable(ctx.getRegister(REG.X86.EDX)) ebx = ctx.convertRegisterToSymbolicVariable(ctx.getRegister(REG.X86.EBX)) keys = [ctx.convertMemoryToSymbolicVariable(MemoryAccess(ADDR_EBP-0x21, 1)) for i in xrange(32)] 

During initialization, we create the context, set the architecture, initialize the registers and memory, and of course, create character variables: the edx and ebx registers and the buffer for the transformed sequence, the values ​​of which will be constrained in the formula.

Now we create the execution trace. To do this, offline download the binary code:

 code = {0x4010EC: '\x55', # push ebp 0x4010ED: '\x8b\xec', # mov ebp, esp 0x4010EF: '\x83\xc4\xdc', # add esp, -24h 0x4010F2: '\xb9\x20\x00\x00\x00', # mov ecx, 20h 0x4010F7: '\xbe\xa8\x93\x40\x00', # mov esi, offset cipher 0x4010FC: '\x8d\x7d\xdf', # lea edi, [ebp+string1] 0x4010FF: '\x8b\x55\x08', # mov edx, [ebp+arg_0] 0x401102: '\x8b\x5d\x0c', # mov ebx, [ebp+arg_4] # loc_401105: 0x401105: '\xac', # lodsb 0x401106: '\x2a\xc3', # sub al, bl 0x401108: '\x32\xc2', # xor al, dl 0x40110A: '\xaa', # stosb 0x40110B: '\xd1\xc2', # rol edx, 1 0x40110D: '\xd1\xc3', # rol ebx, 1 0x40110F: '\xe2\xf4'} # loop loc_401105 

and start processing instructions:

 ip = 0x4010ec while ip < 0x401111: inst = Instruction() inst.setOpcode(code[ip]) inst.setAddress(ip) ctx.processing(inst) ip = ctx.buildSymbolicRegister(ctx.registers.eip).evaluate() 

During the processing of instructions, Triton translates them into symbolic form and adds the resulting symbolic instructions to the context. In this code, we also use the symbolic emulation of the ip register to calculate the next instruction in the order of execution.

After that, it remains to introduce into the context the necessary restrictions on the values ​​of variables. We have this condition for the equality of the converted string with the string “0how4zdy81jpe5xfu92kar6cgiq3lst7”, which we placed in the TEXT constant.

 for i in xrange(32): r_ast = ast.bv(ord(TEXT[i]), 8) l_id = ctx.getSymbolicMemoryId(ADDR_EBP-0x21 + i) l_ast = ctx.getAstFromId(l_id) ex = ast.equal(l_ast, r_ast) expr.append(ex) expr = ast.land(expr) 

Constraints are defined as nodes of an abstract syntax tree (ASD). In our cycle, an ASD node is created for one character from a string and an ASD node for one element of the transformed sequence. Then a new ASD node is created with the operation of comparing these two nodes. Since we need to ensure that the equality conditions for all elements are fulfilled simultaneously, after receiving them in a cycle, they are combined into one SDA under the logical AND operation, expr = ast.land (expr).

Everything is ready to calculate the solution. We obtain the data model for the symbol formula with the given constraints expr.

 model = ctx.getModel(expr) 

You can download the entire keygen script from here .

Run the script and ... nothing happens. Debugging shows that execution loops through the processing of instructions, and it quickly becomes clear that the loop instruction is not being processed. It turns out that Triton does not even know this instruction . How to deal with this problem? You can add the semantics of the new instruction to the Triton source code and rebuild it. But we have already noted that rebuilding on Windows is a rather painstaking job. Hmm, well, let's not get upset right away, and try to redo our code. You can try to replace the loop with the same set of instructions in action, for example:

 dec ecx jz 0401105h 

And you can try to expand the loop manually, and do not process the block with the loop inside, but only the body of the loop as many times as recorded in the ecx register, that is, 32. Then the code will look like this:

 code = ['\xac', # lodsb '\x2a\xc3', # sub al, bl '\x32\xc2', # xor al, dl '\xaa', # stosb '\xd1\xc2', # rol edx, 1 '\xd1\xc3'] # rol ebx, 1 ctx.setConcreteRegisterValue(ctx.registers.esi, ADDR_CIPHER) ctx.setConcreteRegisterValue(ctx.registers.edi, ADDR_EBP - 0x21) ctx.setConcreteRegisterValue(ctx.registers.eip, 0x401105) ctx.setConcreteMemoryAreaValue(ADDR_CIPHER, cipher) ctx.setConcreteMemoryAreaValue(ADDR_TEXT, list(map(ord, TEXT))) edx = ctx.convertRegisterToSymbolicVariable(ctx.registers.edx) ebx = ctx.convertRegisterToSymbolicVariable(ctx.registers.ebx) ip = 0x401105 for i in xrange(32): for c in code: inst = Instruction() inst.setOpcode(c) inst.setAddress(ip) ctx.processing(inst) ip = ctx.buildSymbolicRegister(ctx.registers.eip).evaluate() 

So, we launch a new version. At this time, processing is performed entirely and successfully reaches the calculation of the model in which it is immersed, as expected, for a while. We are waiting ... waiting ... waiting for a very long time. I did not wait. This time, the problem is in the function of calculating the model, and here the error may not be so easy to detect. It can be assumed that the resulting formula is very large, and its calculation can indeed take a very long time. To verify this, reduce the number of iterations in the loop where the processing takes place. Indeed, with a smaller number of iterations, the result is given. By the selection method, it was found that the upper limit of the number of iterations, at which the calculations take the foreseeable time, on an experienced laptop is 12. Yes, this is very small, and as they increase, time grows exponentially. 32 iterations are much more than 12, and it seems that even if you rewrite the code in C ++, it will still be unacceptably long to calculate the model.

If you try to look in debugging, what takes so much time in the getModel function, we will see that these are recursive calls to triton::ast::TritonToZ3Ast::convert .

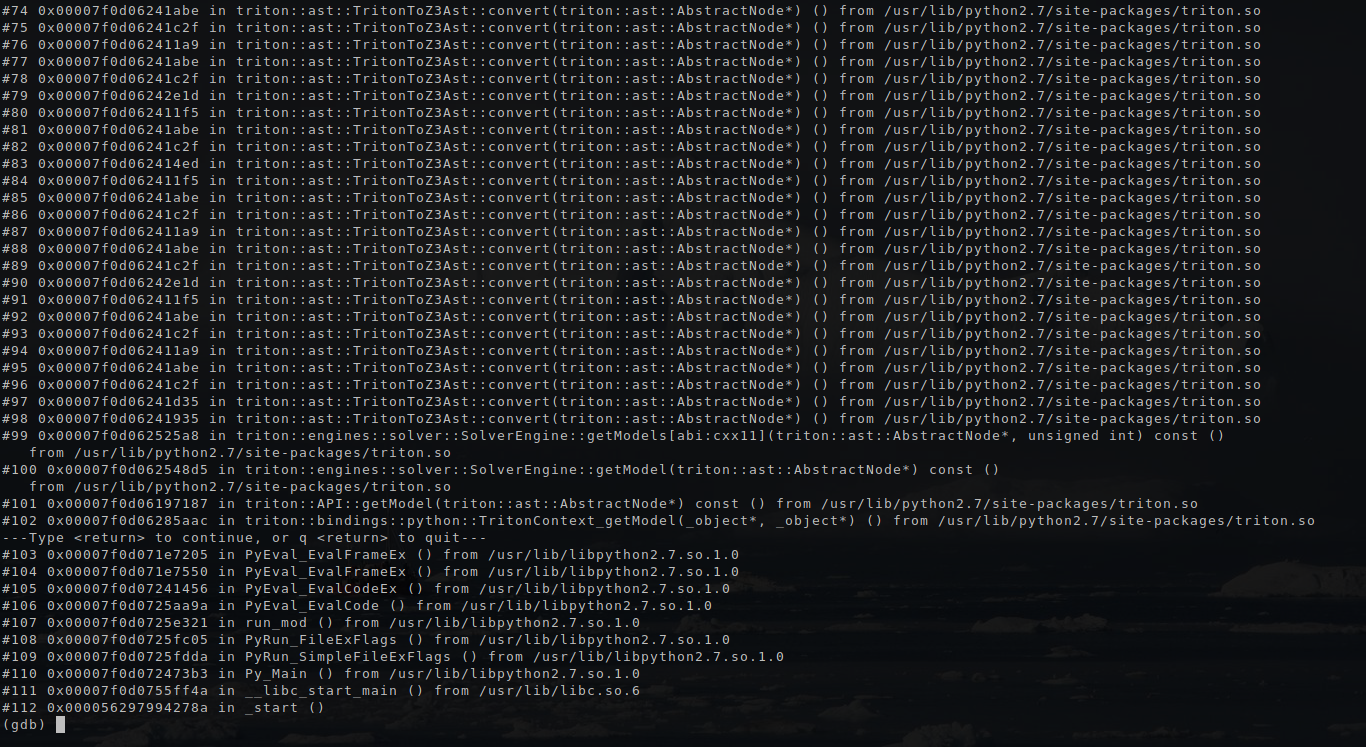
As written in the documentation, Triton uses its custom ASD tree:

An abstract syntax tree (AST) is a representation of a grammar as tree. Triton uses a custom AST for its expressions. AST is available at each program point. - Triton documentation

This function converts Triton's ASD into an expression for z3.
You can try to look at the expressions that make up Triton's SDA. Add the following lines before getting the model:

 tsym = ctx.getSymbolicExpressions() for ek in sorted(tsym.keys()): e = tsym[ek].getAst() print str(e) 

After that, Triton’s expressions will appear in the console:

 ref!0 = SymVar_0 ref!1 = SymVar_1 ref!2 = SymVar_33 ; Byte reference ref!3 = (concat ((_ extract 31 8) (_ bv0 32)) (_ bv29 8)) ; LODSB operation ref!4 = (ite (= (_ bv0 1) (_ bv0 1)) (bvadd (_ bv4232104 32) (_ bv1 32)) (bvsub (_ bv4232104 32) (_ bv1 32))) ; Index operation ref!5 = (_ bv4198662 32) ; Program Counter ref!6 = (concat ((_ extract 31 8) ref!3) (bvsub ((_ extract 7 0) ref!3) ((_ extract 7 0) ref!1))) ; SUB operation ref!7 = (ite (= (_ bv16 8) (bvand (_ bv16 8) (bvxor ((_ extract 7 … 

To get expressions in the SMT-LIB syntax, you need to add another call.

 print ctx.unrollAst(e) 

In this place - unrollAst - the same conversion of Triton's expressions into SMT-LIB expressions takes place, and here you will not wait for completion either, as with the getModel function.
Those familiar with the SMT-LIB syntax will notice that Triton's expressions are SMT-LIB expressions, only in the form of SSA (Single Static Assignment). There is no variable assignment operation in SMT-LIB - they are replaced by the let function operator. But what if you try to independently convert the Triton syntax into the SMT-LIB syntax without deploying the SDA, but replacing the SSA form with a form with let operators, and then try to feed it with z3py? It sounds rather cumbersome and redundant, but it is necessary to get out of this situation, until the developers have finished Triton.

So, with the resulting expression, we perform the following actions:

• Declare variables in the SMT-LIB syntax;
• Replace assignment statements with let statements;
• The resulting expressions are combined into a general formula in SMT-LIB.

The result is a conversion function from the Triton syntax to the SMT-LIB syntax. Of course, it is not universal, but, at least, it works for our task.

 def convert(ctx, asserts): zsym = "" tsym = ctx.getSymbolicExpressions() for ek in sorted(tsym.keys()): e = tsym[ek].getAst() if e.getKind() == AST_NODE.VARIABLE: zsym += "(declare-fun ref!%d () (_ BitVec %d))\n" % (ek, e.getBitvectorSize()) nodes = [] for ek in sorted(tsym.keys()): e = tsym[ek].getAst() if e.getKind() <> AST_NODE.VARIABLE: nodes.append("let ((ref!%d %s))" % (ek, e)) # print reduce(lambda x, y: "%s (%s)" % (x, y), reversed(nodes)) def fold(x, y): if not isinstance(y, list): raise TypeError if len(y) == 1: return y[0] return "%s\n(%s)" % (x, fold(y[0], y[1:])) nodes = ["assert"] + nodes nodes[-1] += '\n' + str(asserts) zsym = zsym + '(' + fold(nodes[0], nodes[1:]) + ')' return zsym 

The result of the function must be sent to the z3py solver for calculation.

 s = z3.Solver() cs = z3.parse_smt2_string(expr) s.assert_exprs(cs) s.check() m = s.model() edx, ebx = m.decls() 

Now the edx and ebx variables store objects of the class z3.z3.FuncDeclRef . We get their numerical representation, and since transformations to quacks are performed after they have been poked with each other, they must also be poxorized.

 edx, ebx = m[edx].as_long(), m[ebx].as_long() print "%x-%x" % (edx, edx ^ ebx) 

The code for the second version can also be taken from the githab .

So, we get a string that you just need to copy in the input field in the crack window. Itching to do it already.

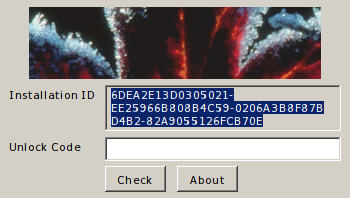
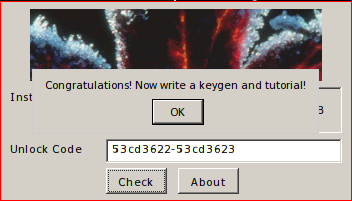
Hooray! Our keygen works correctly.

Ponce

On the basis of Triton built another cool tool - Ponce plugin for IDA Pro. It allows you to do very tempting things - symbolic execution and taint analysis right in the IDA disassembler. Unfortunately, due to the presence of loop instructions in our cracks, we cannot check Ponce on it. Maybe there are people who want to add a loop to Triton? :) Or there is another option. Since kao cracks comes with source code in assembler, you can replace the loop there with the aforementioned similar set of instructions. Then you can use Ponce and feel its power. For an interested reader, this will be a cool task.

findings

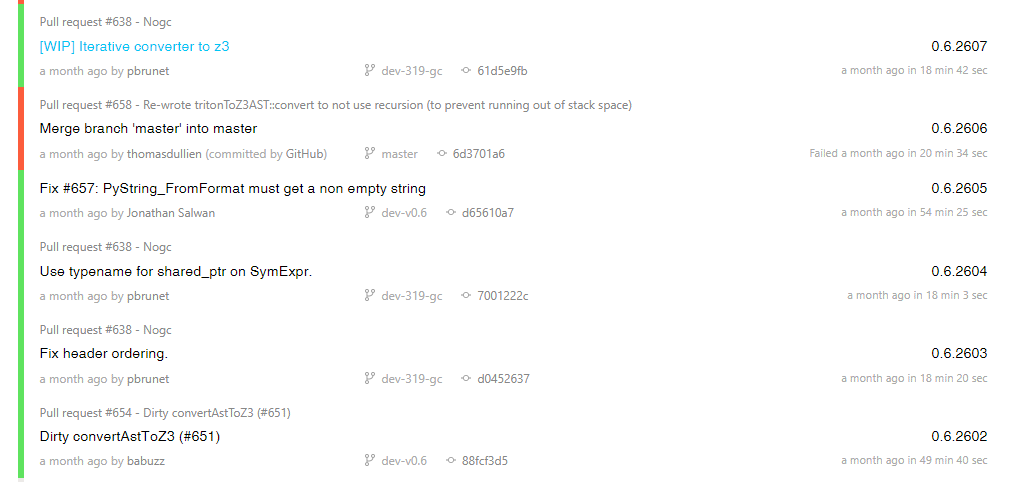
Frankly, Triton did not cope with the task. But let's not be too strict: it is easy to add the loop instruction yourself, and the conversion of the formula, judging by the build history, the developers have already begun to do iterative .

Modern reverse engineering and search for vulnerabilities in software without symbolic execution are a thing of the past. This is proved, for example, by automatic systems for finding vulnerabilities and generating exploits created during the DARPA Cyber ​​Grand Challenge contest. Therefore, tools such as Triton, are now in great demand. As they develop, they become more and more simple to use, so that the symbolic execution becomes a very accessible and effective tool in the work of the researcher.