Quantum Computing: Reference Materials
Do you like cribs? We adore and therefore today we are publishing an article that contains all the most important information about quantum computing. We have collected it from five articles on the topic that came out before. But the most important thing is just a cheat sheet, not a quick-guide for beginners. Beginners are advised to study all the articles entirely, the links are in the list under the cut!

Here you can find information about ground states, gates and matrices, useful mathematical formulas and other information that have already appeared in the publications of this series.
')
Any unitary transformation of the vector | ψ〉 can be visually represented as a simple displacement of a point (marked as | ψ〉) along the Bloch sphere *. Unfortunately, this visual representation is only suitable for one-qubit states: they have not yet come up with a simple generalization for multi-qubit systems. The scope of the Flea is sometimes called the unit sphere.
* To pure states there correspond points on the surface of the sphere, to mixed states - points inside the sphere. A detailed explanation is provided in our publication Basics of Quantum Computing: Pure and Mixed States .
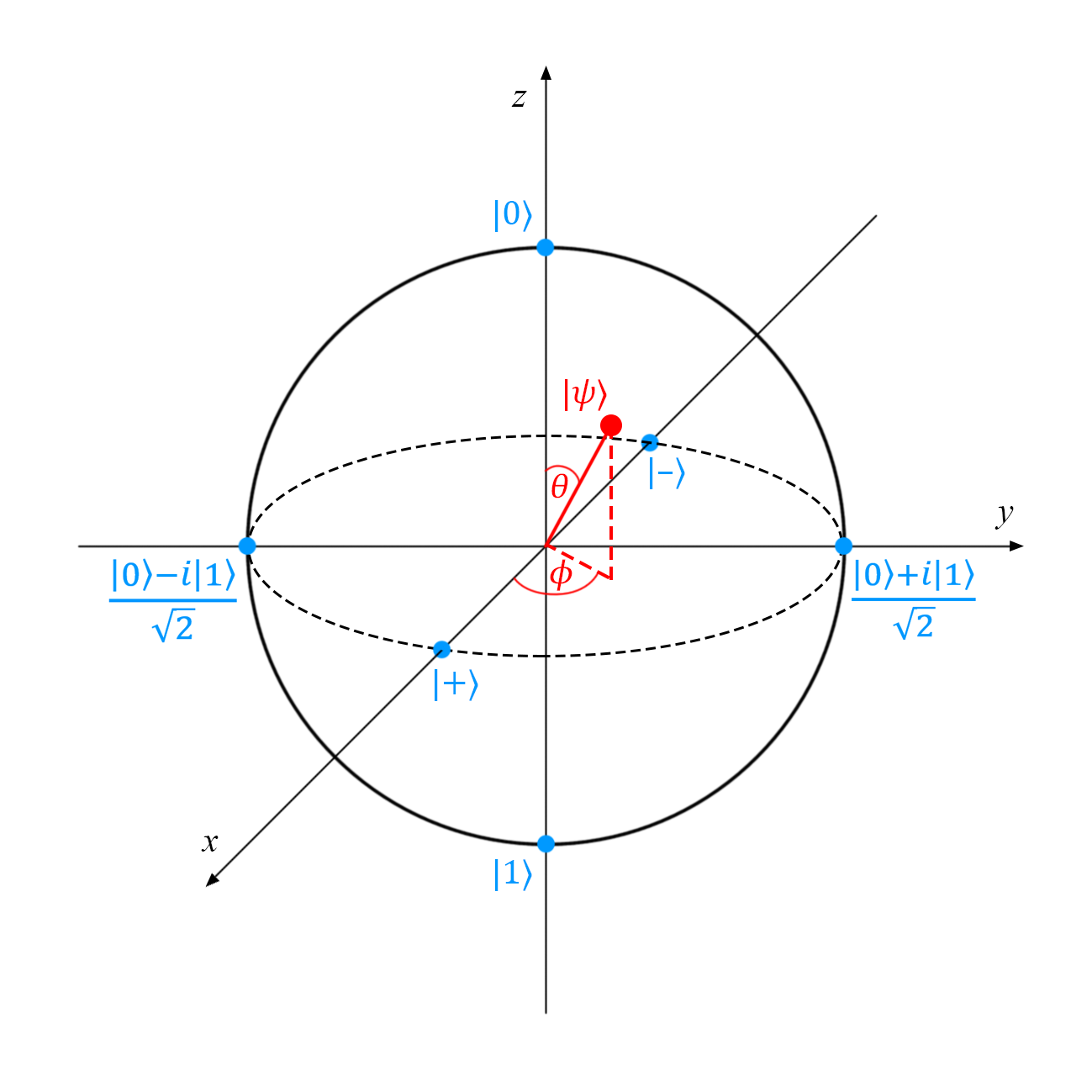
Single qubit states

Bell states (EPR pairs) are the simplest examples of entangled systems consisting of two qubits:
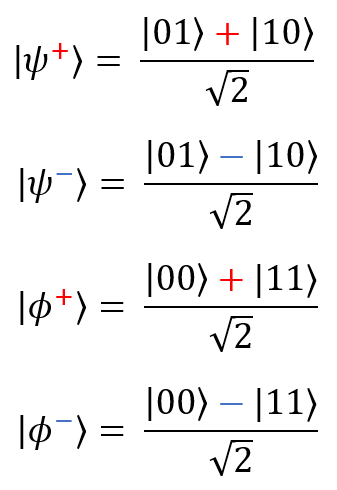
The states of the GHZ (Greenberger – Horn – Zeilinger) in the general form (for n qubits) and in the simplest form (for three qubits):
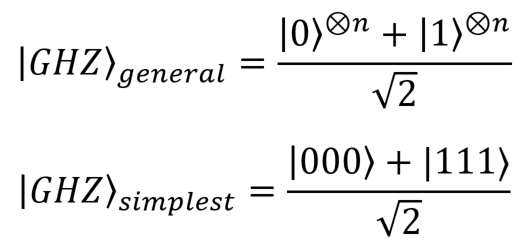
Below is a summary of the most important valves that were presented in our previous publication on valves and circuits . We added information about operations for all one and two-qubit gates (if there are three or more operations, the formulas become too long). In the expressions for controlled valves, the single matrix (II) is highlighted in red, the matrix of the original valve is highlighted in blue, as in a previous publication .
Pauli matrices are reverse to themselves:
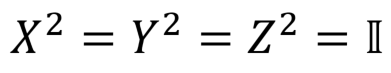
The density operator can be defined as
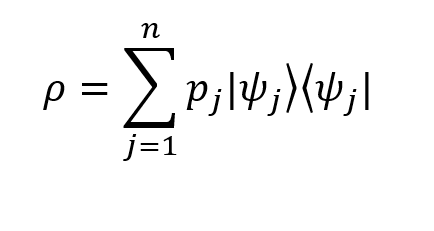
Here:

Articles from the cycle:
Here you can find information about ground states, gates and matrices, useful mathematical formulas and other information that have already appeared in the publications of this series.
')
Table of contents
- Sphere of Flea
- Ground quantum states
- Gates, dies and operations
- Useful relations and equations
Sphere of Flea
Any unitary transformation of the vector | ψ〉 can be visually represented as a simple displacement of a point (marked as | ψ〉) along the Bloch sphere *. Unfortunately, this visual representation is only suitable for one-qubit states: they have not yet come up with a simple generalization for multi-qubit systems. The scope of the Flea is sometimes called the unit sphere.
* To pure states there correspond points on the surface of the sphere, to mixed states - points inside the sphere. A detailed explanation is provided in our publication Basics of Quantum Computing: Pure and Mixed States .

Ground quantum states
Single qubit states


Bell states (EPR pairs) are the simplest examples of entangled systems consisting of two qubits:
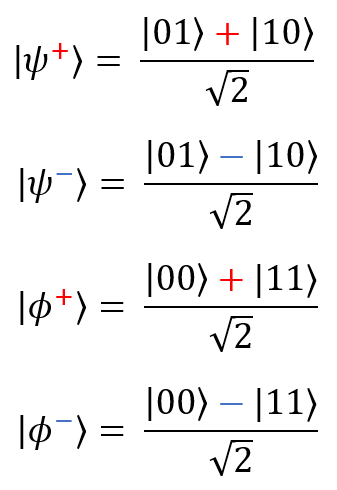
The states of the GHZ (Greenberger – Horn – Zeilinger) in the general form (for n qubits) and in the simplest form (for three qubits):
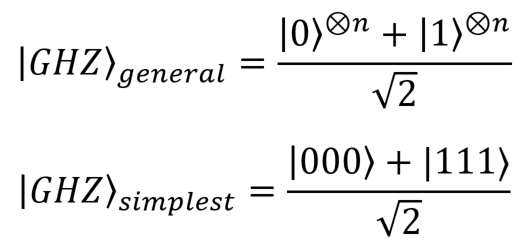
Gates, dies and operations
Below is a summary of the most important valves that were presented in our previous publication on valves and circuits . We added information about operations for all one and two-qubit gates (if there are three or more operations, the formulas become too long). In the expressions for controlled valves, the single matrix (II) is highlighted in red, the matrix of the original valve is highlighted in blue, as in a previous publication .
| Titles | Matrix representation | Legend | Q # presentation | Basic operations |
|---|---|---|---|---|
Pauli gate X, X, NOT, bit switching, 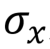 | 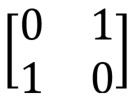 | 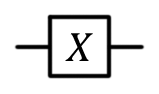 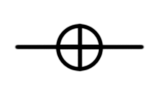 | X (qubit: Qubit) | 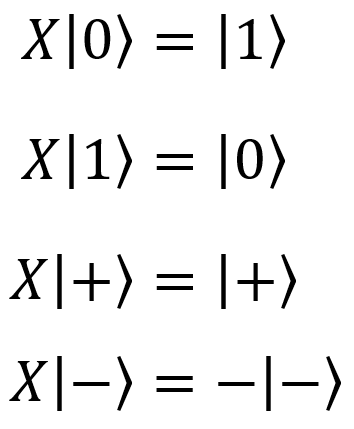 |
Pauli valve Y, Y, 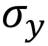 |  |  | Y (qubit: Qubit) | 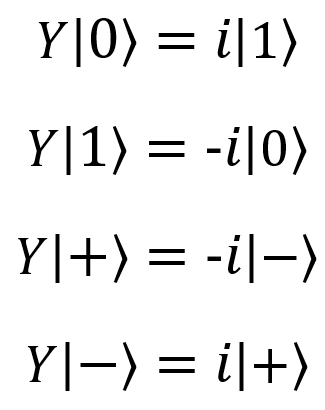 |
Pauli valve Z, Z, phase switching, 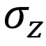 |  |  | Z (qubit: Qubit) | 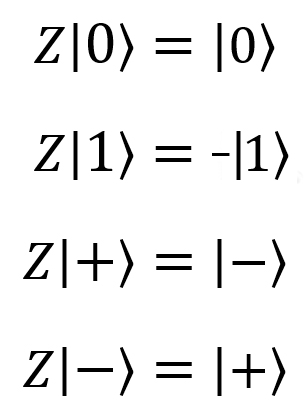 |
| Hadamard valve, H | 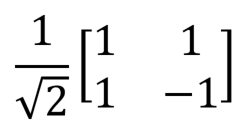 | 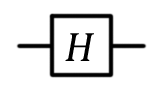 | H (qubit: Qubit) | 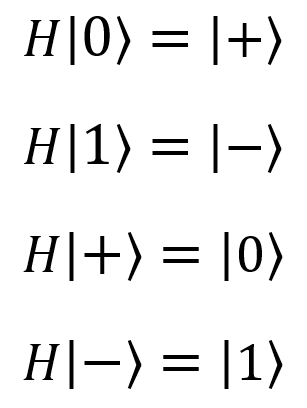 |
Phase shift 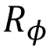 | 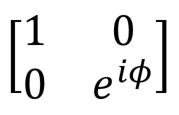 |  | R1 (theta: Double, qubit: Qubit) More generally R (pauli: Pauli, theta: Double, qubit: Qubit) | 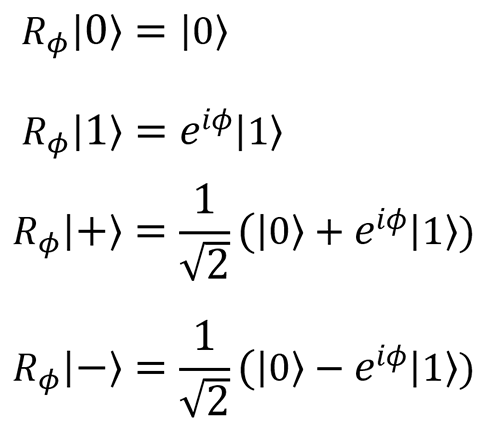 |
Phase shift 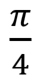 S S | 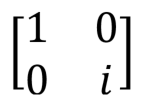 | 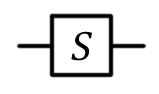 | S (qubit: Qubit) | 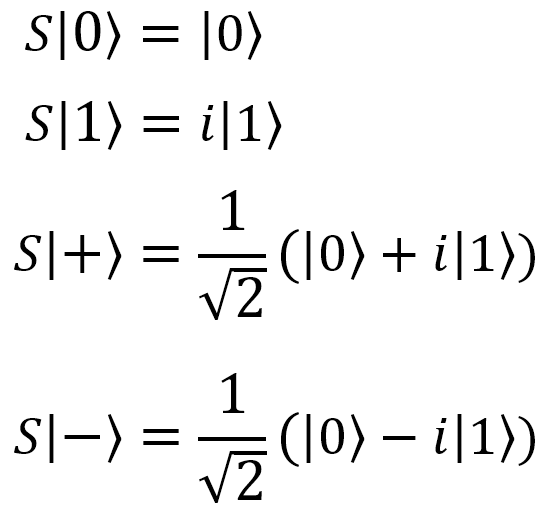 |
 , T , T | 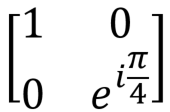 | 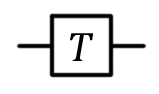 | T (qubit: Qubit) | 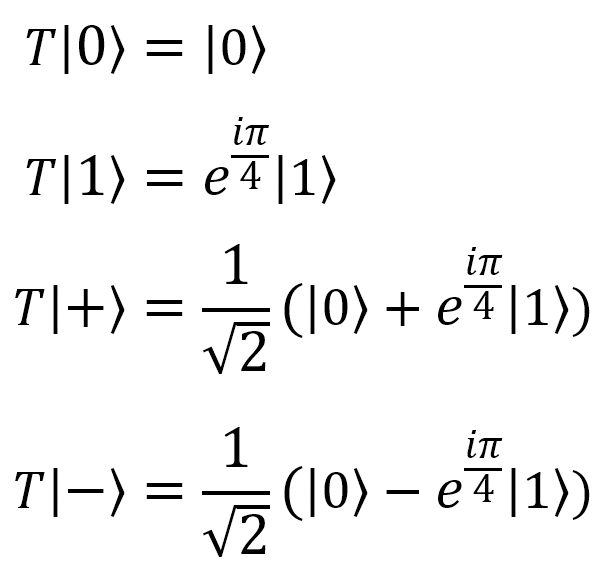 |
| Swap | 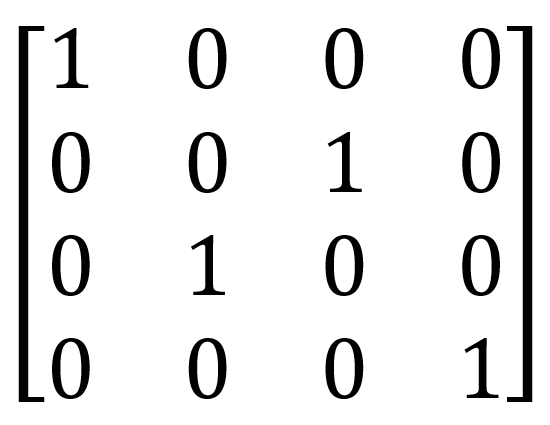 | 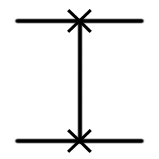 | SWAP (qubit1: Qubit, qubit2: Qubit) | 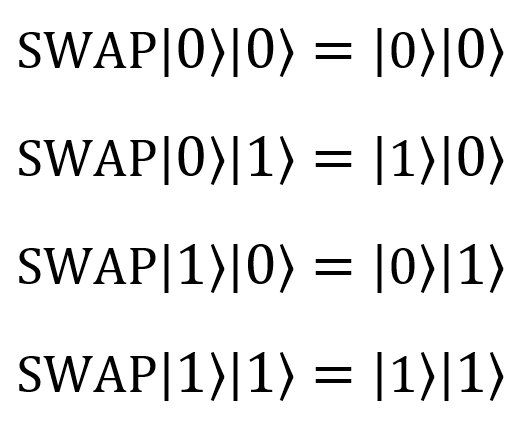 |
| CNOT |  | 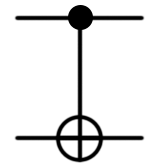 | CNOT (control: Qubit, target: Qubit) or (Controlled X) ([control], (target)); | 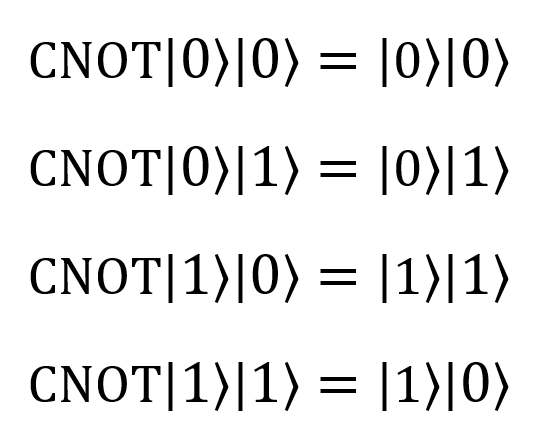 |
| CCNOT, Toffoli valve |  |  | CCNOT (control1: Qubit, control2: Qubit, target: Qubit) or (Controlled X) ([control1; control2], target); | - |
| CSWAP, Fredkin valve |  | 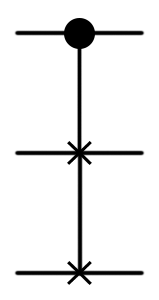 | (Controlled SWAP) ([control], (target)); | - |
Useful relations and equations
Pauli Matrix
Pauli matrices are reverse to themselves:
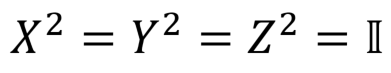
Density operator
The density operator can be defined as
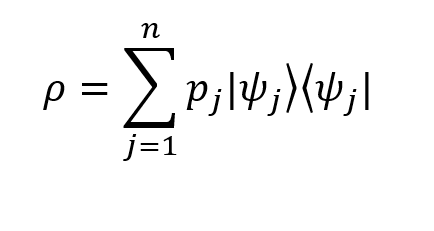
Here:
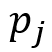 - the probability that the system is in the initial moment of time
- the probability that the system is in the initial moment of time 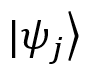 .
.- Element
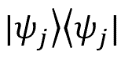 corresponds to the result of the external product of the vector
corresponds to the result of the external product of the vector 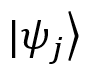 on itself (this transformation is also called the design operator).
on itself (this transformation is also called the design operator). - n is the total number of possible system states (in our example there are 3 of them).
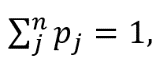 as one would expect (the sum of the probabilities of all possible states is 1).
as one would expect (the sum of the probabilities of all possible states is 1).
Resources
- More information is available on the Microsoft Quantum website.
- Download the Quantum Development Kit
- Subscribe to the Microsoft Quantum Newsletter
- Learn about the latest developments from the Microsoft Quantum blog.
Source: https://habr.com/ru/post/351634/
All Articles