Fundamentals of quantum computing: pure and mixed states
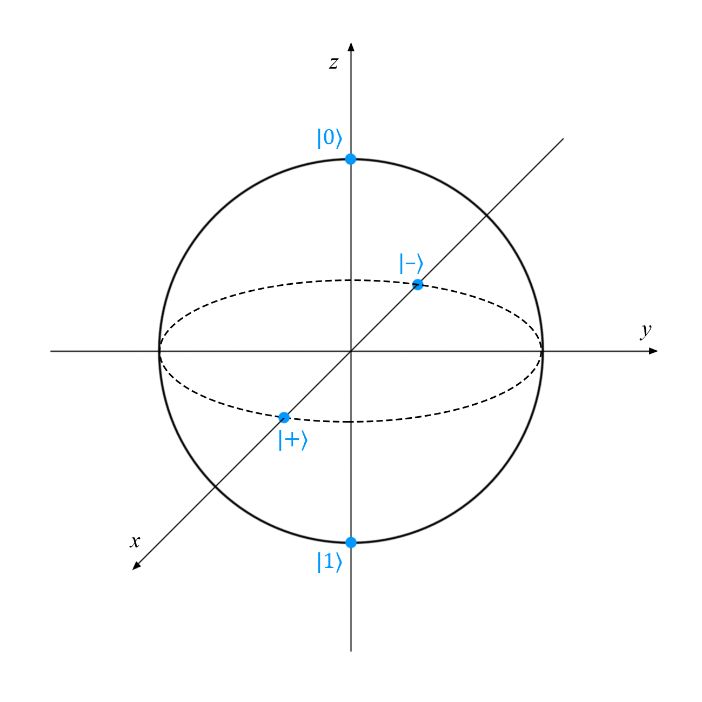
Recently, we talked about the visual representation of single-qubit states - the Bloch sphere. All pure states correspond to points on the surface of the Bloch sphere, and to mixed states, points inside it. In this publication we will try to explain what are in fact pure and mixed states.
A rigorous mathematical explanation is given in the book “Quantum Information and Quantum Computations” by M. Nielsen I. Chang, Section 2.4.1: “Ensembles of Quantum States”, as well as in these remarkable outlines (and corresponding notes of lectures) by Professor Leonard Suskind of Stendford university.
')
A pure state is a state that can be represented by a single state vector | ψι〉. From a practical point of view, this means that at any given time we know (with a probability of 100%) that our system is in the state | ψι〉. In other words, if the system is in a pure state, we have a complete picture of it and know exactly what state it is in.
Examples of pure states: | 0〉, | 1,
, 
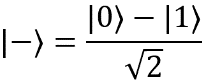. The following points on the surface of the Bloch sphere correspond to them:
If there is no complete picture of the state of the prepared system, then it is said that it is in a mixed state. This situation can be caused by many reasons: for example, incorrect adjustment of laboratory equipment or particle confusion with an external system that is not available to us. However, if the system is in a mixed state, we cannot be 100% sure whether it is in a clean state.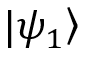
or 
or 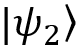in any other possible condition. In this case, the state of the system is described by the probability distribution of all pure states in which it can be with a nonzero probability after preparation.
Consider an example. Suppose our colleague Mary prepared qubits for our experiment. She is trying to sabotage the work and does not tell us what state each qubit is in, but we know that there are only three possible options: these are pure states.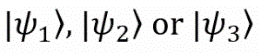
. Therefore, our starting state must be described in the language of probability theory: 
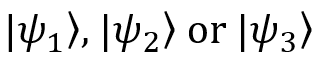. This combination of pure states is called a mixed state.
May we know that Mary (for example) is preparing the state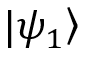 twice as often as 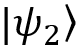or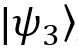 
. We can use this knowledge to describe the probabilities of possible states of our system at the beginning of the experiment. If we do not know exactly how Mary chooses the states being prepared, then we should assume that they are all equally probable. And now it's time to talk about the density matrix (or density operator).
The density operator (ρ) can be used to represent the state of the system, the initial state of which is not known for sure. This operator is a generalization of state vectors (which is used to record pure states). The density matrix for the pure state naturally degenerates into the state vector | ψι〉. For those who are interested, here are some mathematical calculations.
NOTE. It is assumed that the reader has basic concepts of vector and matrix algebra: external and internal product, orthogonality, etc. For acquaintance with them it is recommended to refer to the book of M. Nielsen and I. Chang or to the Standford lectures mentioned at the beginning of the article.
The density operator can be defined as
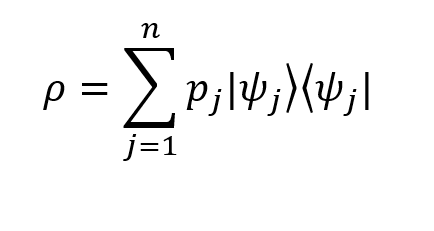
Here :
In our example, the density operator is expanded as follows:
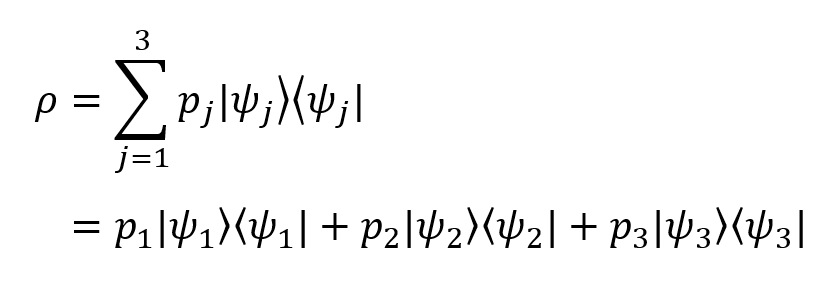
If we substitute the probability values from the above example, we get
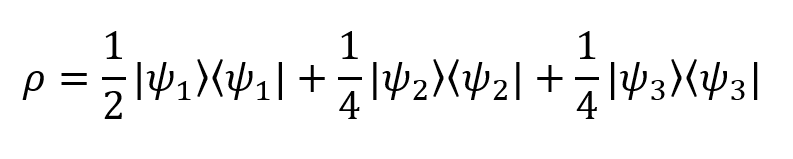
This is the density matrix of our imaginary system! Not so difficult.
Once we have calculated the density operator, it’s very easy to find the probability that the ρ measurement will show some pure quantum state | ψ〉: it is 〈ψ | ρ | ψ〉.
If the state is pure (that is, initially the system can be in only one state), the following equality holds:
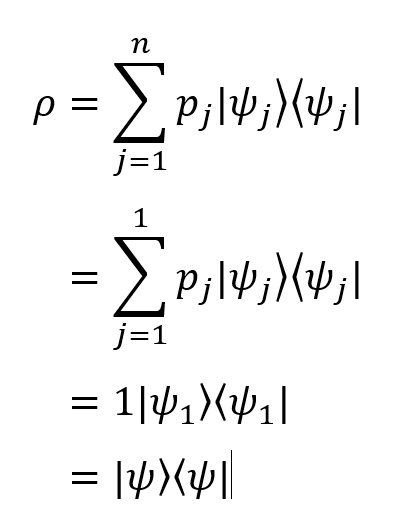
So we get the second, equivalent definition of a pure state: a state in which ρ = |〉 〈ψ | (that is, with a density matrix consisting of a single projector) is clean.
Apply the density operator to our pure state vector:
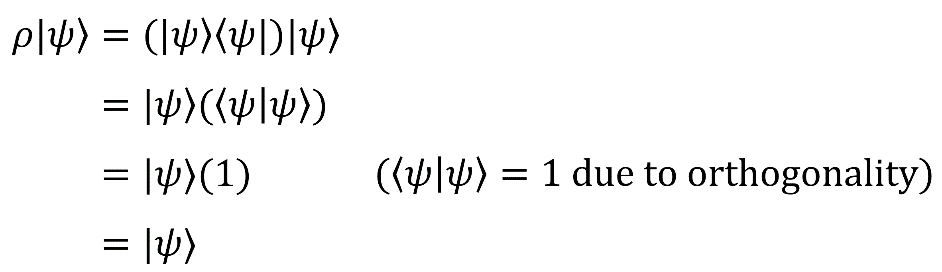
As you can see, the result is only | ψ〉.
By analogy, the probability of detecting a system in a certain state | φ〉 is P = 〈φ | ρ | φ〉 = | 〈φ | ψ〉 | ².
As we see, the rules for calculating probabilities for mixed states are reduced to rules for pure states that we already know. Thus, all the rules for mixed states are expressed through the rules for pure states, as previously stated.
Articles from the cycle:
A rigorous mathematical explanation is given in the book “Quantum Information and Quantum Computations” by M. Nielsen I. Chang, Section 2.4.1: “Ensembles of Quantum States”, as well as in these remarkable outlines (and corresponding notes of lectures) by Professor Leonard Suskind of Stendford university.
')
Pure states
A pure state is a state that can be represented by a single state vector | ψι〉. From a practical point of view, this means that at any given time we know (with a probability of 100%) that our system is in the state | ψι〉. In other words, if the system is in a pure state, we have a complete picture of it and know exactly what state it is in.
Examples of pure states: | 0〉, | 1,
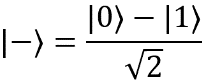, . The following points on the surface of the Bloch sphere correspond to them:Mixed states
If there is no complete picture of the state of the prepared system, then it is said that it is in a mixed state. This situation can be caused by many reasons: for example, incorrect adjustment of laboratory equipment or particle confusion with an external system that is not available to us. However, if the system is in a mixed state, we cannot be 100% sure whether it is in a clean state.
or or in any other possible condition. In this case, the state of the system is described by the probability distribution of all pure states in which it can be with a nonzero probability after preparation.Consider an example. Suppose our colleague Mary prepared qubits for our experiment. She is trying to sabotage the work and does not tell us what state each qubit is in, but we know that there are only three possible options: these are pure states.
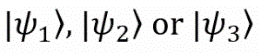. Therefore, our starting state must be described in the language of probability theory: 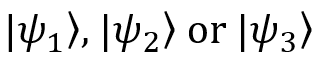. This combination of pure states is called a mixed state.May we know that Mary (for example) is preparing the state
twice as often as or . We can use this knowledge to describe the probabilities of possible states of our system at the beginning of the experiment. If we do not know exactly how Mary chooses the states being prepared, then we should assume that they are all equally probable. And now it's time to talk about the density matrix (or density operator).Density operator, ρ
The density operator (ρ) can be used to represent the state of the system, the initial state of which is not known for sure. This operator is a generalization of state vectors (which is used to record pure states). The density matrix for the pure state naturally degenerates into the state vector | ψι〉. For those who are interested, here are some mathematical calculations.
A bit of math
NOTE. It is assumed that the reader has basic concepts of vector and matrix algebra: external and internal product, orthogonality, etc. For acquaintance with them it is recommended to refer to the book of M. Nielsen and I. Chang or to the Standford lectures mentioned at the beginning of the article.
The density operator can be defined as
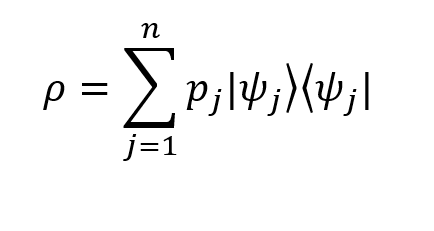
Here :
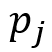- the probability that the system is in the initial moment of time 
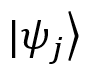.- Element
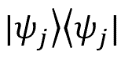corresponds to the result of the external product of the vector 
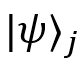on itself (this transformation is also called the design operator). - n is the total number of possible system states (in our example there are three of them).
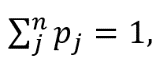, as one would expect (the sum of the probabilities of all possible states is 1).
In our example, the density operator is expanded as follows:
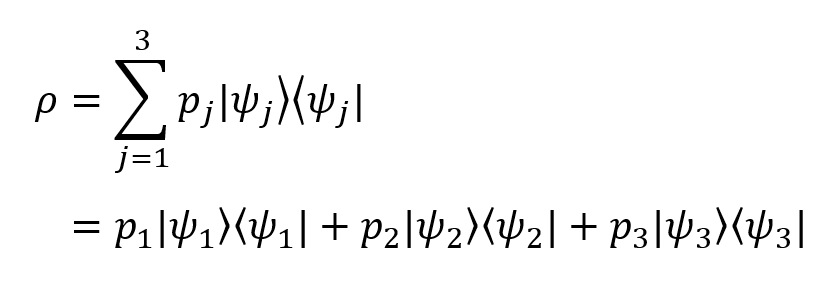
If we substitute the probability values from the above example, we get
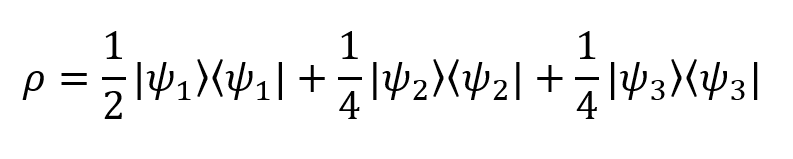
This is the density matrix of our imaginary system! Not so difficult.
Once we have calculated the density operator, it’s very easy to find the probability that the ρ measurement will show some pure quantum state | ψ〉: it is 〈ψ | ρ | ψ〉.
If the state is pure (that is, initially the system can be in only one state), the following equality holds:
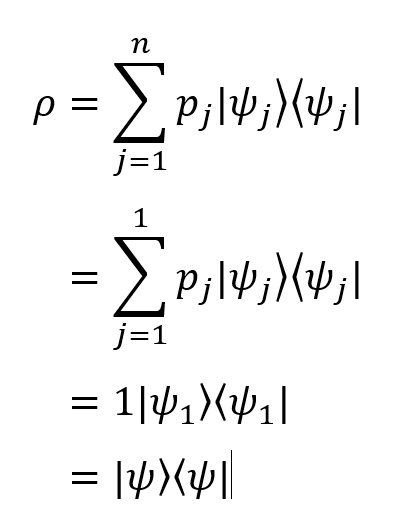
So we get the second, equivalent definition of a pure state: a state in which ρ = |〉 〈ψ | (that is, with a density matrix consisting of a single projector) is clean.
Apply the density operator to our pure state vector:
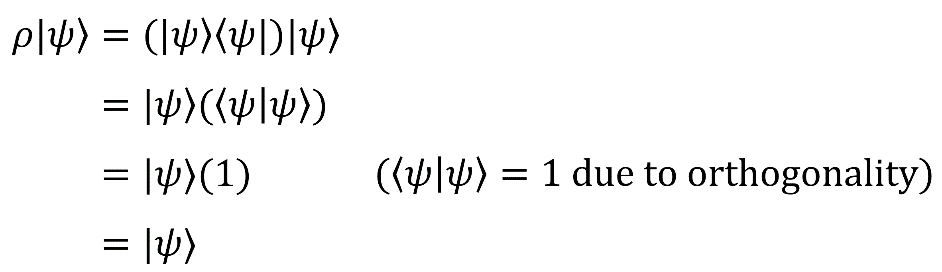
As you can see, the result is only | ψ〉.
By analogy, the probability of detecting a system in a certain state | φ〉 is P = 〈φ | ρ | φ〉 = | 〈φ | ψ〉 | ².
As we see, the rules for calculating probabilities for mixed states are reduced to rules for pure states that we already know. Thus, all the rules for mixed states are expressed through the rules for pure states, as previously stated.
Additional resources
Source: https://habr.com/ru/post/351630/
All Articles