Introduction to quantum computing
Hi, Habr! Most recently, we told you about quantum computing and the Q # language . Today we will go deeper into the theory and consider the history of quantum computing. In addition, in this article you will find 5 requirements for a quantum computer. What properties should have a car of the future? Read under the cut!
As you know, the idea of quantum computing was introduced by Richard Feynman in 1981 during a report at the first conference “Physics of Computing” ( Feynman, 1982 - recommended for familiarization). During the report, Feynman considered a number of difficulties related to the modeling of complex quantum systems using classical computers and put forward the following assumption: to reliably simulate quantum systems, one must strive to create quantum computers.
')
Since then, the scope of quantum computing has evolved very dynamically. Now we have come close to a genuine physical implementation of a scalable quantum computer (for more details, see the following publications).
The most fundamental difference between a classical computer and a quantum one is in the implementation of a bit. Bit (eng. Bit, short for “binary digit” - a binary number) is the minimum unit of digital data. A classical bit at any given time can only take one of two values: 0 or 1. The quantum bit (qubit) obeys the laws of quantum mechanics and therefore can be in a superposition of states 0 and 1.
These classical states 0 and 1 correspond to the Dirac notation | 0 and | 1, and the qubit state formula looks like this:
.
Here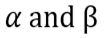
- complex-valued coefficients corresponding to the requirement of normalization 
(this means that the probability of detecting a qubit in one of these two states is 100%, and the probability of detecting it in some other state is 0%).
Insofar as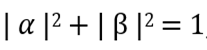
, the wave function | ψ〉 can be rewritten as follows:
As it turns out, the global phase
does not affect the results of experiments, and therefore it can be ignored. However, the local phase 
remains, and the wave function takes the following form:
Writing it in this form, we can represent the superposition of states | 0 and | 1 in visual form using the Bloch sphere:
Now, any unitary transformation of the wave function | ψ〉 can be represented as a simple displacement of a point (it is denoted as | ψ〉) along the surface of the sphere. For example, the state | ψ〉 = | 0〉 corresponds to a point on the z axis, denoted in the figure as | 0. Unfortunately, this visual representation is only suitable for one-qubit states: they have not yet come up with a simple generalization for multi-qubit systems. In this series of articles we will return to the field of Bloch.
The phenomena of superposition and entanglement * allow you to perform certain operations using quantum computers faster than is possible (according to modern concepts) using classical computing systems. Examples of such operations are the decomposition of numbers into prime factors ( Shor, 1997 ) and searching for unstructured data ( Grover, 1997 ). Moreover, thanks to these unique quantum mechanical features, whole new fields of science and technology appear - for example, quantum cryptography ( Bennett & Brassard, 1984 ). In the next section, we will look at the requirements for such systems.
* Superposition is a phenomenon in which the state of a quantum system is described by a probability distribution of possible states of a single qubit, for example,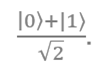
. A state of entanglement requires two or more qubits (or, more generally, degrees of freedom). Einstein described this phenomenon as “eerie effect at a distance” - the interrelation of two particles, in which an operation on one of them can affect the state of the other, regardless of the distance and physical barriers between them (however, the prohibition to transmit information with superluminal speed remains ). An example of a state of entanglement is the Bell state:
In 2008, David Divinchenzo formulated five conditions (they represent a revised version of an article from 1996 ) that a system must meet in order to be considered a scalable quantum computer . We will use these conditions as a basis for further discussions in this series of publications. Below I give their general formulations (a detailed discussion is given in the original article).
A quantum computer should allow increasing the set of qubits to a number sufficient for complex calculations. A “well-described” name is a qubit, the properties and interactions of which with other parts of the system are well known.
By the beginning of the calculations, the system should be in a simple, exactly known state. If we are unable to re-bring the system to this simple initial state (initialize it), then it cannot be considered as a computer at all.
For a number of reasons (for example, due to interaction with external systems), the qubit system is difficult to maintain in a prepared state long enough before it “decorates” because of the appearance of unwanted interactions between the system and its unknown and uncontrolled environment. After decoherence of a quantum system, the results of measurements of quantum bits (0 and 1) will be described not by a quantum distribution, but by a statistical one. It is impossible to restore the decoded state by any quantum operations. Therefore, the period for which the system enters the decoherent state should be much longer than the time required to perform operations on the valves.
A universal is a set of gates, sufficient to perform any quantum computation. Here is the minimum required set of operations: moving single qubits to any point on the Bloch sphere (using single-qubit gates) and entangling system components (this requires multi-qubit gates). For example, a universal set includes a Hadamard valve, a phase shift valve, a CNOT valve, and a π8 valve. With their help, you can perform any quantum computation on an arbitrary set of qubits.
It is necessary to be able to obtain the result of calculations by reading the final state of individual qubits.
There are two additional requirements for quantum communication - they relate to the processing of quantum information:
Currently, active work is underway on several physical models of quantum computing: ion traps, photon qubits, topological qubits, etc. Whatever the basic physical principles, a quantum computer must comply with the five fundamental (and two additional) principles outlined above. .
In a subsequent publication, we will look at some of these potential quantum computers, but first we need to get acquainted with quantum gates and circuit diagrams. My next article will be devoted to them. See you next time!
Articles from the cycle:
Introduction
As you know, the idea of quantum computing was introduced by Richard Feynman in 1981 during a report at the first conference “Physics of Computing” ( Feynman, 1982 - recommended for familiarization). During the report, Feynman considered a number of difficulties related to the modeling of complex quantum systems using classical computers and put forward the following assumption: to reliably simulate quantum systems, one must strive to create quantum computers.
')
Since then, the scope of quantum computing has evolved very dynamically. Now we have come close to a genuine physical implementation of a scalable quantum computer (for more details, see the following publications).
The most fundamental difference between a classical computer and a quantum one is in the implementation of a bit. Bit (eng. Bit, short for “binary digit” - a binary number) is the minimum unit of digital data. A classical bit at any given time can only take one of two values: 0 or 1. The quantum bit (qubit) obeys the laws of quantum mechanics and therefore can be in a superposition of states 0 and 1.
These classical states 0 and 1 correspond to the Dirac notation | 0 and | 1, and the qubit state formula looks like this:
.
Here
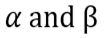- complex-valued coefficients corresponding to the requirement of normalization (this means that the probability of detecting a qubit in one of these two states is 100%, and the probability of detecting it in some other state is 0%).
Insofar as
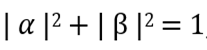, the wave function | ψ〉 can be rewritten as follows:
As it turns out, the global phase
does not affect the results of experiments, and therefore it can be ignored. However, the local phase remains, and the wave function takes the following form:
Writing it in this form, we can represent the superposition of states | 0 and | 1 in visual form using the Bloch sphere:
Now, any unitary transformation of the wave function | ψ〉 can be represented as a simple displacement of a point (it is denoted as | ψ〉) along the surface of the sphere. For example, the state | ψ〉 = | 0〉 corresponds to a point on the z axis, denoted in the figure as | 0. Unfortunately, this visual representation is only suitable for one-qubit states: they have not yet come up with a simple generalization for multi-qubit systems. In this series of articles we will return to the field of Bloch.
The phenomena of superposition and entanglement * allow you to perform certain operations using quantum computers faster than is possible (according to modern concepts) using classical computing systems. Examples of such operations are the decomposition of numbers into prime factors ( Shor, 1997 ) and searching for unstructured data ( Grover, 1997 ). Moreover, thanks to these unique quantum mechanical features, whole new fields of science and technology appear - for example, quantum cryptography ( Bennett & Brassard, 1984 ). In the next section, we will look at the requirements for such systems.
* Superposition is a phenomenon in which the state of a quantum system is described by a probability distribution of possible states of a single qubit, for example,
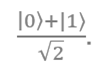. A state of entanglement requires two or more qubits (or, more generally, degrees of freedom). Einstein described this phenomenon as “eerie effect at a distance” - the interrelation of two particles, in which an operation on one of them can affect the state of the other, regardless of the distance and physical barriers between them (however, the prohibition to transmit information with superluminal speed remains ). An example of a state of entanglement is the Bell state:
Five requirements for a quantum computer (and two additional)
In 2008, David Divinchenzo formulated five conditions (they represent a revised version of an article from 1996 ) that a system must meet in order to be considered a scalable quantum computer . We will use these conditions as a basis for further discussions in this series of publications. Below I give their general formulations (a detailed discussion is given in the original article).
1. The physical system must be scalable, and the state of the qubits must be known.
A quantum computer should allow increasing the set of qubits to a number sufficient for complex calculations. A “well-described” name is a qubit, the properties and interactions of which with other parts of the system are well known.
2. A quantum computer must allow to reliably prepare sets of qubits in a simple initial state (for example, | 000 ...)
By the beginning of the calculations, the system should be in a simple, exactly known state. If we are unable to re-bring the system to this simple initial state (initialize it), then it cannot be considered as a computer at all.
3. The system must have sufficient durability to perform operations on qubits.
For a number of reasons (for example, due to interaction with external systems), the qubit system is difficult to maintain in a prepared state long enough before it “decorates” because of the appearance of unwanted interactions between the system and its unknown and uncontrolled environment. After decoherence of a quantum system, the results of measurements of quantum bits (0 and 1) will be described not by a quantum distribution, but by a statistical one. It is impossible to restore the decoded state by any quantum operations. Therefore, the period for which the system enters the decoherent state should be much longer than the time required to perform operations on the valves.
4. The system should allow the implementation of a “universal set” of valves.
A universal is a set of gates, sufficient to perform any quantum computation. Here is the minimum required set of operations: moving single qubits to any point on the Bloch sphere (using single-qubit gates) and entangling system components (this requires multi-qubit gates). For example, a universal set includes a Hadamard valve, a phase shift valve, a CNOT valve, and a π8 valve. With their help, you can perform any quantum computation on an arbitrary set of qubits.
5. The system must support the measurement of individual qubits.
It is necessary to be able to obtain the result of calculations by reading the final state of individual qubits.
There are two additional requirements for quantum communication - they relate to the processing of quantum information:
- The system must have the ability to reliably convert data stored as stationary (computational) qubits into network (transmitted) qubits (for example, photons) and back.
- The system must have the ability to correctly transfer network qubits between endpoints.
Currently, active work is underway on several physical models of quantum computing: ion traps, photon qubits, topological qubits, etc. Whatever the basic physical principles, a quantum computer must comply with the five fundamental (and two additional) principles outlined above. .
In a subsequent publication, we will look at some of these potential quantum computers, but first we need to get acquainted with quantum gates and circuit diagrams. My next article will be devoted to them. See you next time!
Additional resources
- Author page on GitHub.
- Personal blog of the author.
- Posted on LinkedIn .
- Microsoft Quantum .
- Microsoft Quantum Development Kit .
- Microsoft Quantum blog .
- Telegram-channel of Stas Pavlov with news from the world of quantum computers Qubit (Quantum Daily) .
- The nearest event on the topic is DotNext (St. Petersburg, April 22-23), speaker Rolf Huisman (Microsoft MVP), a report on Programming quantum computers in .NET using Microsoft Q # .
Source: https://habr.com/ru/post/351624/
All Articles