About probabilities

( source )
Sometimes I have to tell other people how machine learning works and, in particular, neural networks. I usually start with gradient descent and linear regression, gradually moving to multilayer perceptrons, auto-encoders and convolutional networks. Everyone nods their heads knowingly, but at some point someone shrewd is sure to ask:
And why is it so important that the variables in the linear regression are independent?
or
And why exactly convolutional networks are used for images, but not ordinary fully connected ones?
“Oh, it's simple,” I want to answer. - "because if the variables were dependent, then we would have to model the conditional probability distribution between them" or "because in a small local area it is much easier to learn the joint distribution of pixels." But here’s the problem: my listeners still don’t know anything about probability distributions and random variables, so you have to get out in other ways, explaining more difficult, but with fewer concepts and terms. And what to do if they are asked to tell about normalization or generative models about batch, I won’t even think for it.
So let's not torture ourselves and others and just remember the basic concepts of probability theory.
Random variables
Imagine that we have profiles of people, where their age, height, sex and number of children are indicated:
| age | height | gender | children |
|---|---|---|---|
| 32 | 175 | one | 2 |
| 28 | 180 | one | one |
| 17 | 164 | 0 | 0 |
| ... | ... | .... | .... |
Each line in such a table is an object. Each cell is the value of a variable characterizing this object. For example, the age of the first person is 32 years, and the growth of the second is 180cm. And what if we want to describe some variable at once for all our objects, i.e. take a whole column? In this case, we will have not one specific value, but several at once, each with its own frequency of occurrence. The list of possible values + the corresponding probability is called a random variable (random variable, rv).
Discrete and continuous random variables
To put this in my head, I will repeat once again: a random variable is completely defined by the probability distribution of its values. There are 2 main types of random variables: discrete (discrete) and continuous (continuous).
Discrete variables can take a set of clearly separable values. I usually portray them like this (probability mass function, pmf):
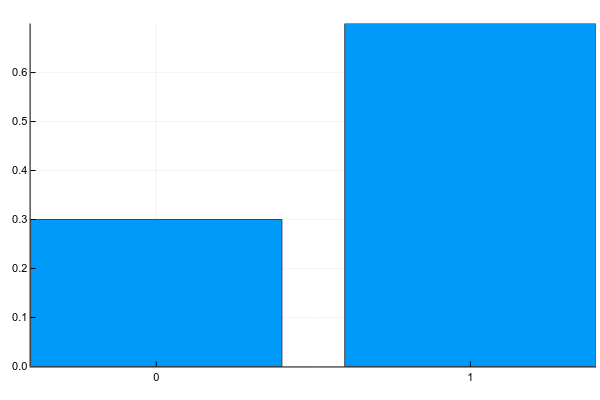
Pkg.add("Plots") using Plots plotly() plot(["0","1"], [0.3, 0.7], linetype=:bar, legend=false) And the text is usually written like this (g - gender):
p(g=0)=0.3p(g=1)=0.7
Those. the probability that a randomly taken person from our sample will be a woman ( g=0 ) is equal to 0.3, and a man ( g=1 ) - 0.7, which is equivalent to the fact that in the sample there were 30% of women and 70% of men.
Discrete variables include the number of children in a person, the frequency of occurrence of words in the text, the number of views of the film, etc. The result of classification into a finite number of classes, by the way, is also a discrete random variable.
Continuous variables can take any value in a certain interval. For example, even if we record that a person’s height is 175 cm, i.e. rounded up to 1 centimeter, in fact, it can be 175.8231cm. They represent continuous variables usually using a probability density function (pdf):
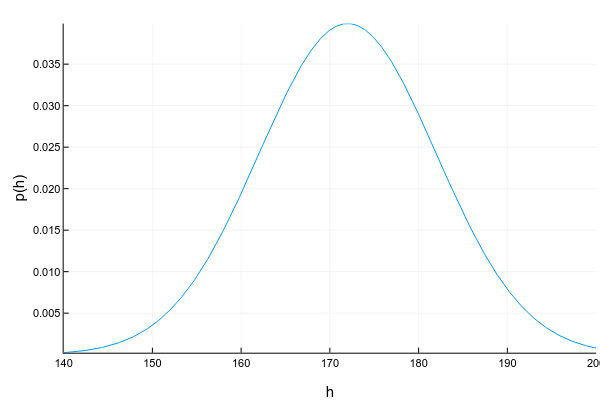
Pkg.add("Distributions") using Distributions xs = 140:0.1:200 ys = [pdf(Normal(172, 10), x) for x in xs] plot(xs, ys; xlabel="h", ylabel="p(h)", legend=false, show=true) The probability density graph is a tricky thing: unlike the probability mass graph for discrete variables, where the height of each column directly shows the probability of obtaining such a value, the probability density shows the relative amount of probability around a certain point. The probability itself in this case can be calculated only for the interval. For example, in this example, the probability that a randomly taken person from our sample will be between 160 and 170 cm tall is about 0.3.
d = Normal(172, 10) prob = cdf(d, 170) - cdf(d, 160) Question: can the probability density at some point be greater than one? The answer is yes, of course, the main thing is that the total area under the graph (or, mathematically speaking, the integral of the probability density) is equal to unity.
Another difficulty with continuous variables is that it is not always possible to describe their probability density beautifully. For discrete variables, we simply had a table of value -> probability. For continuous, this is no longer a ride, since, generally speaking, they have an infinite set of values. Therefore, they usually try to approximate the dataset by some well-studied parametric distribution. For example, the graph above is an example of a so-called. normal distribution. The probability density for it is given by the formula:
p(x)= frac1 sqrt2 pi sigma2e− frac(x− mu)22 sigma2
Where mu (mat. expectation, mean) and sigma2 (variance, variance) - distribution parameters. Those. Having only 2 numbers, we can fully describe the distribution, calculate its probability density at any point or the total fidelity between two values. Unfortunately, there is not a distribution for any data set that can describe it beautifully. There are many ways to deal with this (take at least a mixture of normal distributions ), but this is a completely different topic.
Other examples of continuous distribution are: age of a person, intensity of a pixel in an image, response time from a server, etc.
Joint, marginal and conditional distribution
Usually we consider the properties of an object not one by one, but in combination with others, and here the notion of joint distribution of several variables appears. For two discrete variables, we can portray it as a table (g - gender, c - # of children):
| c = 0 | c = 1 | c = 2 | |
|---|---|---|---|
| g = 0 | 0.1 | 0.1 | 0.1 |
| g = 1 | 0.2 | 0.4 | 0.1 |
According to this distribution, the probability of finding a woman with 2 children in our data set is equal to p(g=0,c=2)=0.1 , and a childless man - p(g=1,c=0)=0.2 .
For two continuous variables, such as height and age, we will again have to set the analytical distribution function p(h,a) by approximating it,
for example, multidimensional normal . You can't write it down with a table, but you can draw:
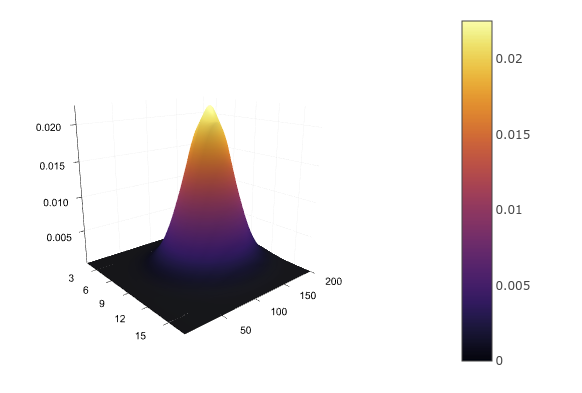
d = MvNormal([172.0, 30.0], [10 0; 0 5]) xs = 160:0.1:180 ys = 22:1:38 zs = [pdf(d, [x, y]) for x in xs, y in ys] surface(zs) Having a joint distribution, we can find the distribution of each variable separately, simply by summing up (in the case of discrete) or integrating (in the case of continuous) the remaining variables:
p(g)= sumcp(g,c)p(h)= intp(a,h)da
This can be represented as a summation over each row or column of a table and putting the result on the table fields:
| c = 0 | c = 1 | c = 2 | ||
|---|---|---|---|---|
| g = 0 | 0.1 | 0.1 | 0.1 | 0.3 |
| g = 1 | 0.2 | 0.4 | 0.1 | 0.7 |
So we get again p(g=0)=0.3 and p(g=1)=0.7 . The margining process gives a name to the most distributable distribution — marginal probability.
But what if we already know the value of one of the variables? For example, we see that we are in front of a man and want to get a probability distribution of the number of his children? The joint probability table will help us here too: since we already know for sure that we are a man, i.e. g=1 , we can throw out from consideration all other options and consider only one line:
| c = 0 | c = 1 | c = 2 | |
|---|---|---|---|
| g = 1 | 0.2 | 0.4 | 0.1 |
barp(c=0|g=1)=0.2 barp(c=1|g=1)=0.4 barp(c=2|g=1)=0.1
Since the probabilities must be summed up in one way or another, the resulting values need to be normalized, and then we get:
p(c=0|g=1)=0.29p(c=1|g=1)=0.57p(c=2|g=1)=0.14
The distribution of one variable with a known value of the other is called conditional (conditional probability).
Chain rule
And all these probabilities are connected by one simple formula, which is called a chain rule (chain rule, not to be confused with the rule of differentiation):
p(x,y)=p(y|x)p(x)
This formula is symmetric, so you can also:
p(x,y)=p(x|y)p(y)
The interpretation of the rule is very simple: if p(x) - the likelihood that I will go to a red light, and p(y|x) - the probability that a person switching to a red light will be shot down, then the joint probability of going on a red light and being shot down is exactly equal to the product of the probabilities of these two events. But generally go to the green better.
Dependent and independent variables
As already mentioned, if we have a table of joint distribution, then we know everything about the system: you can calculate the marginal fidelity of any variable, you can conditional distribution of one variable with another known, etc. Unfortunately, in practice it is impossible to compile such a table (or calculate the parameters of continuous distribution). For example, if we want to calculate the joint distribution of the occurrence of 1000 words, we will need a table from
107150860718626732094842504906000181056140481170553360744375038837035105112493612
249319837881569585812759467291755314682518714528569231404359845775746985748039345
677748242309854210746050623711418779541821530464749835819412673987675591655439460
77062914571196477686542167660429831652624386837205668069376
(slightly more than 1e301) cells. For comparison, the number of atoms in the observable universe is approximately 1e81. Perhaps, buying an additional strap of memory is not enough.
But there is one nice detail: not all variables depend on each other. The probability of whether it will rain tomorrow will hardly depend on whether I turn the road to a red light. For independent variables, the conditional distribution of one from the other is simply a marginal distribution:
p(y|x)=p(y)
To be honest, the joint probability of 1000 words is written as follows:
p(w1,w2,...,w1000)=p(w1) timesp(w2|w1) timesp(w3|w1,w2) times... timesp(w1000|w1,w2,...)
But if we "naively" assume that the words are independent of each other, the formula will turn into:
p(w1,w2,...,w1000)=p(w1) timesp(w2) timesp(w3) times... timesp(w1000)
And to save probabilities p(wi) for 1000 words you need a table with only 1000 cells, which is quite acceptable.
Why then do not consider all variables independent? Alas, so we lose a lot of information. Imagine that we want to calculate the probability that a patient has the flu, depending on two variables: sore throat and fever. Separately, a sore throat can talk about both the disease and the fact that the patient was just singing loudly. Separately, the fever can talk about both the disease and the fact that the person has just returned from a run. But if we simultaneously observe the temperature and sore throat, then this is already a serious reason for the patient to be discharged from hospital.
Logarithm
Very often in the literature one can see that not just probability is used, but its logarithm. What for? Everything is pretty prosaic:
- Logarithm is a monotonically increasing function, i.e. for any p(x1) and p(x2) if a p(x1)>p(x2) , then logp(x1)> logp(x2) .
- The logarithm of the product is equal to the sum of logarithms: log(p(x1)p(x2))= logp(x1)+ logp(x2) .
In the example with the words, the probability of meeting any word p(wi) As a rule, much less than one. If we try to multiply a lot of small probabilities on a computer with limited accuracy of calculations, guess what will happen? Yeah, very quickly our probabilities are rounded off to zero. But if we add a lot of individual logarithms, then it will be almost impossible to go beyond the limits of accuracy of calculations.
Conditional probability as a function
If after all these examples you have the impression that the conditional probability is always calculated by counting the number of times that a certain value is met, then I hasten to dispel this error: in the general case, the conditional probability is a function of one random variable from another:
p(y|x)=f(x)+ epsilon
Where epsilon - this is some noise. Types of noise are also a separate topic, which we will not get into now, but on the function f(x) let's stop in more detail. In the examples with discrete variables above, as a function, we used a simple calculation of the occurrence. This in itself works well in many cases, for example, in the naive Bayes classifier for text or user behavior. A slightly more complicated model is linear regression:
p(y|x)=f(x)+ epsilon= theta0+ sumi thetaixi+ epsilon
Here, too, it is assumed that the variables xi independent of each other but the distribution p(y| mathbfx) already modeled using a linear function whose parameters mathbf theta Need to find.
The multilayer perceptron is also a function, but thanks to intermediate layers that are affected by all input variables at once, MLP allows you to simulate the dependence of the output variable on the input combination, and not just on each of them separately (remember the example of a sore throat and temperature).
The convolutional network works with the distribution of pixels in the local area covered by the size of the filter. Recurrent networks model the conditional distribution of the next state from the previous and input data, as well as the output variable from the current state. Well, in general, you get the idea.
Bayes theorem and multiplication of continuous variables
Remember the network rule?
p(x,y)=p(y|x)p(x)=p(x|y)p(y)
If we remove the left side, we get a simple and obvious equality:
p(y|x)p(x)=p(x|y)p(y)
And if we now transfer p(x) to the right, we get the famous Bayes formula:
p(y|x)= fracp(x|y)p(y)p(x)
An interesting fact: the English pronunciation of "Bayes" in English sounds like the word "bias", i.e. "bias". But the surname of the scientist "Bayes" reads like "base" or "bayes" (it is better to listen to Yandex Translate).
The formula is so battered that every part of it has its own name:
- p(y) is called the prior distribution (prior). This is what we know even before we saw a particular object, for example, the total number of people who repaid the loan on time.
- p(x|y) bears the name of likelihood. This is the probability to see such an object (described by the variable x ) with this value of the output variable y . For example, the likelihood that a person who has given a loan has two children.
- p(x)= intp(x,y)dy - marginal likelihood, the probability of seeing such an object at all. It is the same for everyone. y , so it is most often not considered, but simply maximizing the numerator of the Bayes formula.
- p(y|x) - posterior distribution. This is the probability distribution of the variable. y after we saw the object. For example, the likelihood that a person with two children will give the loan on time.
Bayesian statistics are terribly interesting, but we will not get into it now. The only question that I would like to touch upon is the multiplication of two distributions of continuous variables, which we find, for example, in the numerator of the Bayes formula, and indeed in every second formula over continuous variables.
Suppose we have two distributions p1(y) and p2(y) :
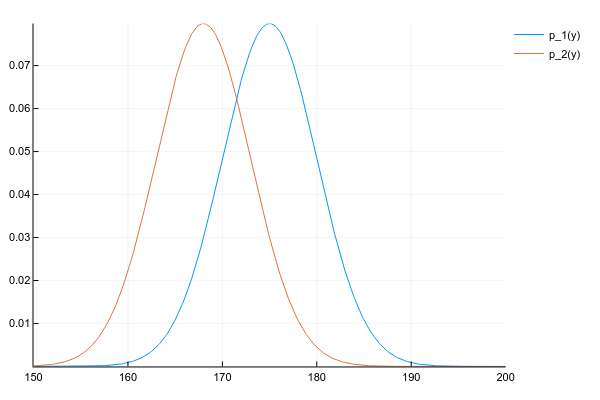
d1 = Normal(175, 5) d2 = Normal(168, 5) space = 150:0.1:200 y1 = [pdf(d1, y) for y in space] y2 = [pdf(d2, y) for y in space] plot(space, y1, label="p_1(y)") plot!(space, y2, label="p_2(y)") And we want to get their product:
p(y)=p1(y)p2(y)
We know the probability density of both distributions at each point, so, honestly and in general, we need to multiply the densities at each point. But, if we behaved well, then p1(y) and p2(y) we are given parameters, for example, for a normal distribution of 2 numbers - the expectation and variance, and for their product will have to consider the probability at each point?
Fortunately, the product of many well-known distributions provides another well-known distribution with easily computable parameters. The key word here is conjugate prior .
No matter how we calculate, the product of two normal distributions gives another normal distribution (albeit not normalized):
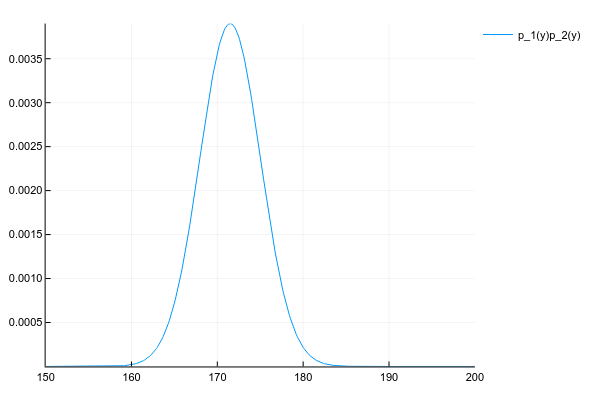
# # , plot(space, y1 .* y2, label="p_1(y)p_2(y)") Well, just for comparison, the distribution of the mixture of 3 normal distributions:

plot(space, [pdf(Normal(130, 5), x) for x in space] .+ [pdf(Normal(150, 20), x) for x in space] .+ [pdf(Normal(190, 3), x) for x in space]) Questions
Since this is a tutorial and someone will certainly want to remember what was written here, here are a few questions for securing the material.
Let a person's height be a normally distributed random variable with parameters mu=172 and sigma2=10 . What is the probability to meet a person exactly 178cm tall?
The correct answers can be considered "0", "infinitely small" or "undefined". And all because the probability of a continuous variable is considered at some interval. For a point, the interval is its width, depending on where you studied mathematics, the length of a point can be considered zero, infinitely small, or not defined at all.
Let be x - the number of children in the borrower of the loan (3 possible values), y - a sign of whether a person has given a loan (2 possible values). We use the Bayes formula to predict whether a particular customer with one child will give a loan. How many possible values can take a priori and a posteriori distribution, as well as likelihood and marginal likelihood?
The table of joint distribution of two variables in this case is small and looks like:
| c = 0 | c = 1 | c = 2 | |
|---|---|---|---|
| s = 0 | p (s = 0, c = 0) | p (s = 0, c = 1) | p (s = 0, c = 2) |
| s = 1 | p (s = 1, c = 0) | p (s = 1, c = 1) | p (s = 1, c = 2) |
Where s - a sign of a successful loan.
The Bayes formula in this case is:
p(s|c)= fracp(c|s)p(s)p(c)
If all values are known, then:
- p(c) - this is the marginal probability of seeing a person with one child, counted as the sum of the column c=1 and is just a number.
- p(s) - a prior / marginal probability that a randomly taken person, about whom we do not know, will give a loan. May have 2 values corresponding to the sum of the first and the second row of the table.
- p(c|s) - credibility, conditional distribution of the number of children depending on the success of the loan. It may seem that since this is a distribution of the number of children, then there should be 3 possible values, but this is not so: we already know for sure that a person with one child came to us, therefore we consider only one column of the table. But the success of the loan is still in question, so there are 2 options - 2 lines of the table.
- p(s|c) - a posteriori distribution, where we know c , but we consider 2 possible options s .
Neural networks that optimize the distance between two distributions q(x) and p(x) , often used as an optimization goal, cross-entropy (cross entropy) or Kullback-Leibler divergence. The latter is defined as:
KL(q||p)= intq(x) log fracq(x)p(x)dx
intq(x)(.)dx - this is mate. waiting by q(x) and why in the main part - log fracq(x)p(x) - division is used, not just the difference between the densities of the two functions q(x)−p(x) ?
log fracq(x)p(x)= logq(x)− logp(x)
In other words, this is the difference between densities, but in a logarithmic space that is computationally more stable.
')
Source: https://habr.com/ru/post/351400/
All Articles