Negative selection of personnel in the hierarchical structure of the enterprise

Introduction

We all know how important the selection of personnel in the organization. But often we have rather vague ideas about how exactly the structure of the organization affects the efficiency of this personnel. Or, for example, how the distribution of employees with different parameters in the staffing table affects the work efficiency.

When this question is raised, these are usually some kind of common words, heuristics from boring textbooks with qualitative descriptions , such as the hierarchical structure pushing forward and motivating daffodils who are more interested in their own progress than in the prosperity of the enterprise.

It turns out that some aspects of this question are fairly easy to simulate mathematically, which can open up opportunities for new options for managing companies. Under the conditions of fairly simple assumptions about the properties of personnel, a huge number of important and interesting properties crawl out by themselves, simply by setting the structure of the organization. And then the question can be put like this - Is there an opportunity to use this for the benefit of the organization?
')

Model Description

Step by step how the large organization develops. $$$O$ in which each working person at each level of the hierarchy is described by two variables and two subsets:

$$

$$H_i = \ {C, D, E, W_i \},$$

Where $$$\ {... \}$ - lots of, $$$S$ - the set of all the chiefs of this person, $$$D$ - The set of all subordinates of a given person.

$$$W_i$ - the degree of personal effectiveness (productivity) of how a person performs his tasks on $$$i$ m level At each level $$$W_i = U (0,1) + 0.5$ where $$$U (0,1)$ - uniform distribution. Thus, the average personal productivity of all together is 1. It is appropriate to recall the principle of Peter , who, in the case of this task of effectiveness, begins to sound like this: “In the hierarchical system, each individual tends to rise to the lower level of his incompetence.” That is, not the fact that a person is not effective even higher. It just rises just to where he has a failure in efficiency. The most effective collective farm chairman is not always even a tolerable milkmaid, as we know. However, as we shall see later, this principle also describes an absolutely idealistic situation (especially since it was justly criticized ).
$$$E = U (0,1)$ - the degree of human selfishness. By selfishness, here we mean only some kind of “distilled” ability to do things that are not related to productivity or the performance of work functions, but in the opinion of a person should contribute to his career advancement.

In the organization model is generated $$$N$ a person with the characteristics described above, which are initially randomly distributed over $$$L$ levels. The capacity of each level is set from the following considerations:

We all know the joke about mathematicians who order a beer in a bar , asking half of what the previous one asked for:

$$

$$\ sum_ {i = 1} ^ {\ infty} {\ frac {1} {2 ^ i}} = 1$$

So for $$$i$ -th level the number of people at the level can be calculated by the following formula:

$$

$$N_i = \ lfloor \ frac {N} {S \ cdot 2 ^ i} + 0.5 \ rfloor, S = \ sum_ {i = 1} ^ {L} {\ frac {1} {2 ^ i}}.$$

Where $$$\ lfloor x \ rfloor$ - rounding down (floor). $$$S$ - the normalization amount to get exactly the final $$$N$ person.

Accordingly, the entire organization $$$O$ set as a dimension vector $$$L$ where $$$i$ level is given by many employees $$$O_i = \ {H_i ^ 1, H_i ^ 2, ..., H_i ^ {N_i} \}.$

Each person has a set of chiefs (except for the upper level) and a set of subordinates (except for the lower level) - $$$C, D$ . To set this list for each person, we use the following algorithm:

Let organization be given $$$O$ . Then for each person $$$H \ in O$ also owned $$$O_i$ list $$$D$ of $$$K$ subordinates are given as follows:

HD=[] if Hi != 0: HD = random.shuffle(O[i-1])[:K] for dependant in HD: dependant.C.append(H) 

It turns out a graph expanding from the top of the hierarchy in the spirit of a tree, but not a tree, because there can be more than one path between two vertices.

At each iteration, the performance of each person $$$H_i$ is calculated according to the following formula:

$$

$$P_ {H_i} = (1-E ^ K) \ cdot W_i \ cdot min (1 \ cup P_D),$$

Where $$$P_D = \ {P_ {D_0}, P_ {D_1}, ... \}$ - a lot of productivity of all subordinates. The essence of this formula is that the egoism of individual subordinates is leveled by their number. $$$K$ while the overall system performance without selfishness is the performance of the weakest link in submission $$$min (1 \ cup P_D)$ .

Further, at each iteration, the performance of all people is considered:

$$

$$P = \ sum_ {i = 0} ^ {N} {P_i}.$$

As the main measure of the effectiveness of the structure, productivity normalized to the number of people is used: $$$P '= P / N$ . This indicator shows how much the obtained result is less than what should have been obtained if no one was an egoist and the productivity of each would be equal to 1.

At the end of each iteration, a frame advance stage occurs. Every turn $$$R$ random people are fired (retire or something else), after which their direct subordinates compete for the vacant places, and the very bottom of the pyramid is added $$$R$ laid off with the hierarchy lowered to the bottom level. This is done in order not to introduce new entities and to avoid additional random walks of the result.

Three modifications of the competition were considered:

1. Scenario with selfish progress, when promotion depends only on the egoism of the employee,
   
2. A scenario with idealistic progress, when promotion depends only on employee productivity at the level of a displaced boss,
   
3. The mixed promotion scenario, the more complex promotion model, described below.
   

Scenario with selfish progress
The competition lies in the fact that every direct subordinate of the dismissed has the opportunity to participate in the struggle for advancement with some probability. The winner is considered in accordance with the following formula:

$$

$$Winner = max (E_ {D_H} * Rnd (K)),$$

Where $$$E_ {D_H}$ - vector of all egoisms in subordinates $$$D_H$ former chief $$$H$ , * - elementwise multiplication, $$$Rnd (K)$ - vector of random values ​​from $$$U (0,1)$ dimensions $$$K$ .

Scenario with idealistic advancement
The winner is considered in accordance with the following formula:

$$

$$Winner = max (W_ {D_H, i} * Rnd (K)),$$

Where $$$W_ {D_H, i}$ - vector of all potential performance of subordinates $$$D_H$ for $$$i$ level of the former chief $$$H$ .

Mixed Promotional Scenario
It was proposed to take the model of competition adopted in one of the developed countries. “The pyramid is divided into two halves. From below, the advance correlates with performance. From above, advancement is determined by the product of egoism and total performance down the chain. The transition from the lower to the upper half is pure egoism. ”

It can be implemented like this:

 prob = [] center = round(L/2) for D in HD: if Di<center: prob.append(DE + DW) elif Di == center: prob.append(DE) else: prob.append(DE*(D.P+Col(D))) s = sum(prob) r = random.random() for p in prob: r = r - p/s if r<0: winner = HD[i] 

The Col (D) function is a recurrent function that summarizes the performance of all the subject subordinates:

 def Col(H): result = 0 for D in HD: result += DP + Col(D)    return result 

What happens with the simulation?

Scenario with selfish progress
Consider the result of the calculation according to the scenario with egoistic advancement, where 60 iterations are lived for a population of 10,000 people. The first chart is how performance changes over the years. It is worth noting that the value of 1 would be only if all employees had perfect efficiency at all levels. And second, this is how the distribution of egoists changes over the years (you can see that initially all egoists are at the level of 20% of the entire population of the level, which seems to be quite optimistic).



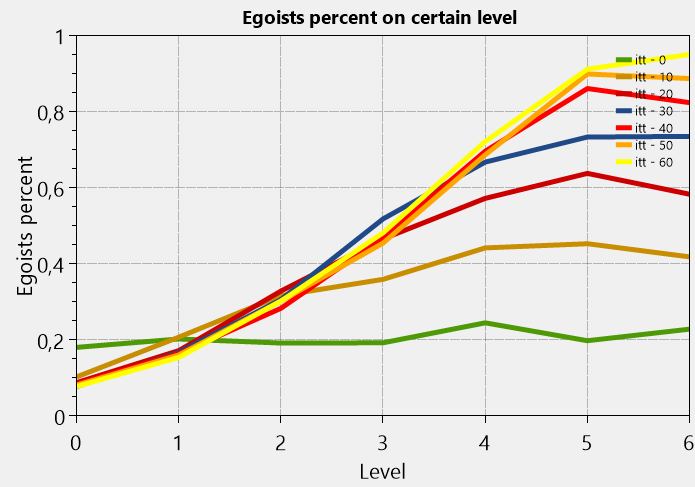
Productivity is more than doubled. The number of egoists in the upper levels is growing, exponentially striving to completely fill the upper levels.

Well, the obvious conclusion is that the number of egoists at the upper levels is growing, and productivity is falling, because egoism is not always combined with good performance. Who would doubt that.

Scenario with idealistic advancement
All the same options. 10,000 people, 60 iterations, 20% of egoists at any level at the beginning. In the code one line is changed. The criterion by which the competition for the place. Instead of selfishness, there is now a level of potential performance at the level of a displaced boss. In the particular case it turns out like this.



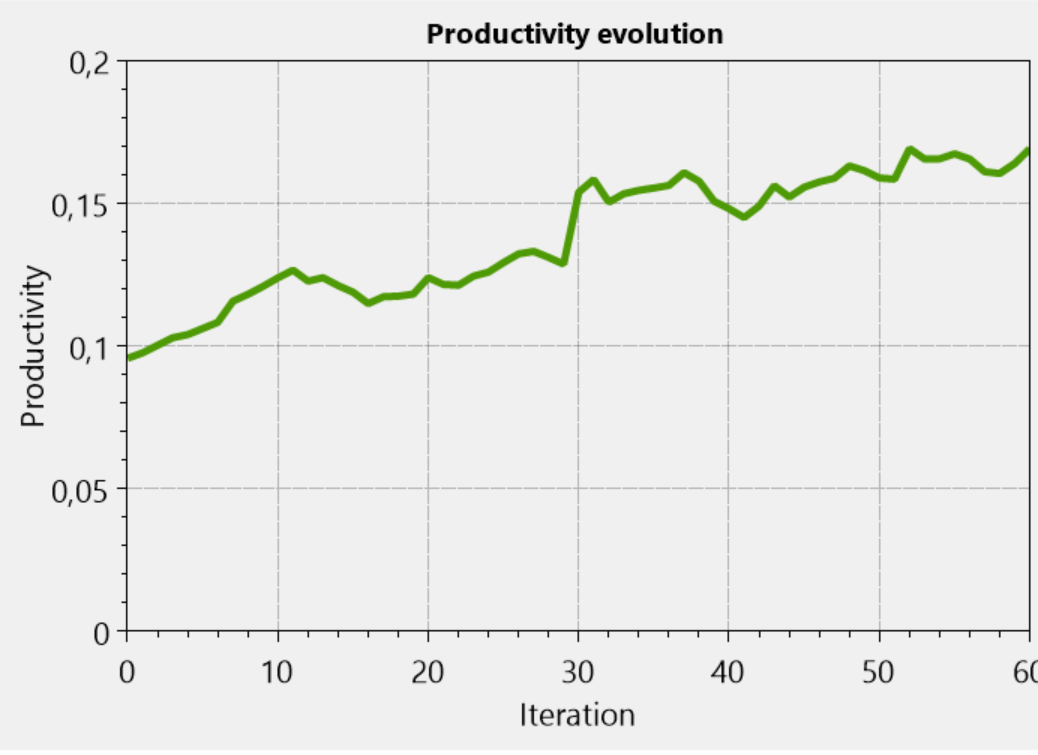
Since the level of egoism is not correlated in any way with the level of productivity, the redistribution of productive people to the upper levels does not affect the egoism of this level. But at the same time, the productivity of all grows due to the promotion of the talented.

Mixed Promotional Scenario
The parameters are the same. Just another rule. Complicated scheme of separation of assessment of different levels of hierarchy



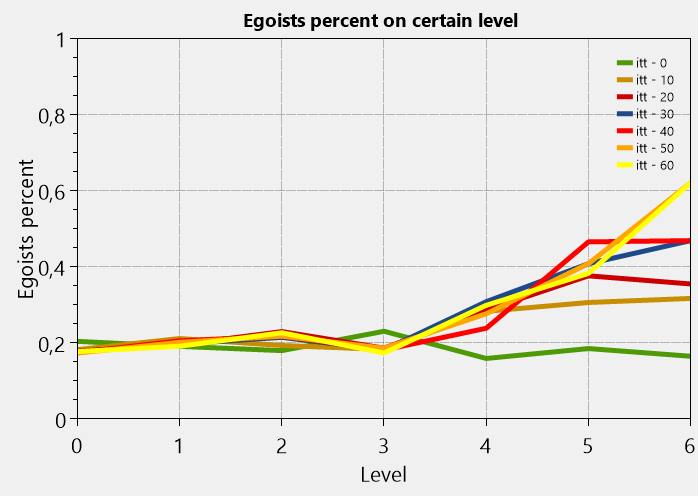
As can be seen, in such an organization the number of egoists on the board is also growing, but not to such glaring values ​​as in the selfish scenario. Moreover, the process does not converge to 1 at the highest level. Accordingly, the drop in productivity from the dominance of selfishness is much lower. Up to 0.06, not up to 0.04, as in the selfish way.

Generalizations and confidence intervals

A number of questions may arise about how exactly these graphs may vary, depending on the different implementations of the random process. Maybe there is no such big difference between egoism and a mixed version? Just two maximally different implementations.

To do this, each of the scenarios was driven 20 times with the same parameters. After that, graphs with confidence intervals for the average of each process are plotted. Results on the chart.


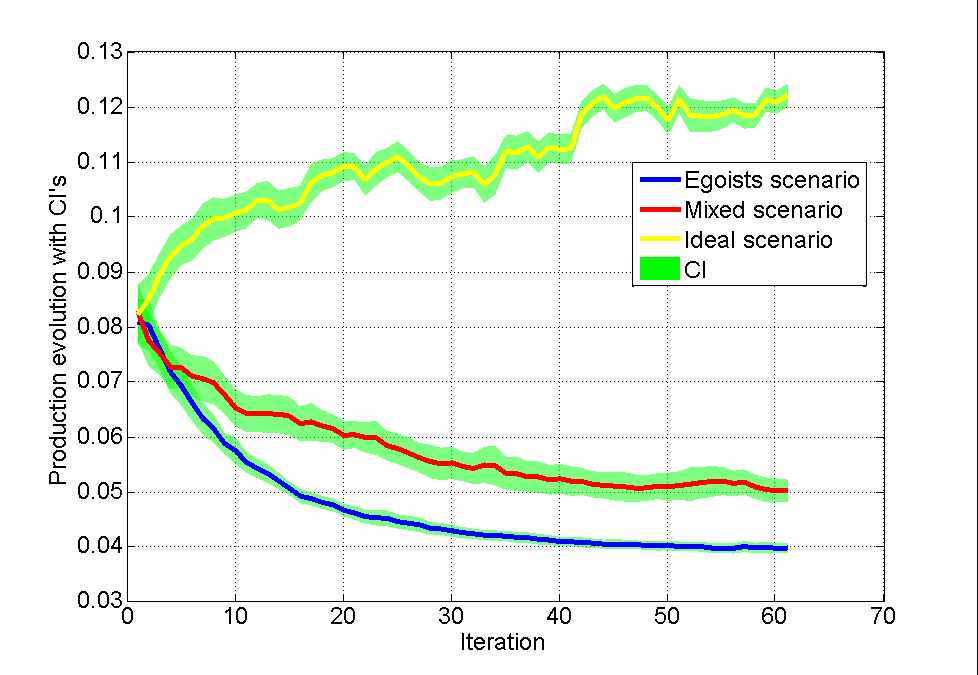
It may be noted a number of interesting features of these dependencies.
Confidence intervals for the selfish scenario are narrower than in other cases. This is because the process after the second iteration is quite homogeneous. Some significant number of people with random performance characteristics will fall to a higher level than they will ensure a decrease in performance to all their subordinates. This is because on the one hand they are selfish enough to make it even higher than they were. On the other hand, in the graph there is a fairly wide branching and connectedness of the grid of subordination, which will create a situation where the egoists will be more likely to get into one of the “competitions” for a new place higher in the hierarchy. And with each level, this probability is more and more, until the top level is filled with the most desperate egoists. At this point, the process will begin to converge.

The reason for the wide confidence interval of the mixed version is explained (for the most part) by the fact that for this structure, the rotation of personnel at the highest levels rather quickly “throws off” the egoists, who generate inefficient production chains. A person selfishly reached the top level and nothing prevented him, and then suddenly (after another increase) his decisions make the work of a huge number of subordinates ineffective. And at the very next iteration, this person does not win the promotion with respect to a more productive opponent. And when this happens, the improvement happens rather spasmodically, which can be seen on the chart with a particular case (however, sometimes a decrease happens the same way). In principle, the scheme itself is not directly ideal, but we see a significant difference with egoism.

findings

Uncontrolled promotion of employees can cause significant harm to the company and contribute to the degradation and reduce efficiency. As shown above, the algorithm chosen by the enterprise for personnel rotation significantly affects the work of the entire organization.

In this article, we tried to give readers the opportunity to see and see the problem where it was possible no one had noticed before, and also to formulate it as an applied task, which may have a number of adequate solutions.

But it is obvious that an idealistic model with the promotion of only effective at the new level of employees is not very realistic. Problems begin with the question, how to understand - will the employee be effective in a new position? What are his talents? Therefore, at this stage, we are not entitled to throw tips, how to optimize the situation. Transferring model implementations to a specific real structure is always an extremely delicate thing and requires a fair amount of practical tests and evidence of the effectiveness of such a transfer.

However, finally, it would be appropriate to recall that in 2010 the Snobel Prize was given to researchers from Italy, who, using the Peter principle, proved that the most effective algorithm of advancement (if this principle is adequate to reality) would be the promotion of a random employee chosen by the random generator numbers It’s probably completely random, probably not worth it, but perhaps it would be more useful for everyone to choose a random from the short list. But it is not exactly.

---

Article author: Alexander Bespalov, Data scientist, Maxilect

PS We publish our articles on several runet sites. Subscribe to our pages on the VK , FB or Telegram channel to learn about all our publications and other news from Maxilect.