Count Joseph Flavius: whom to kill first

Long ago, during the time of the Roman Empire, a group of Jewish soldiers was surrounded by the Roman army. The choice is small - to surrender or die. Sly Jews invented a system so as not to give up alive and not commit a sin of suicide. And so on until only one is left alive, and he will have to commit suicide. In the story I heard, the hero, Joseph , wanted to save his life and surrender, not die. And so he decided to find a cherished place.

(At the time of writing the post dofiga painted soldiers).

“I was in high school when Professor Phil told me to solve this problem.
He proposed to solve it manually, on paper. Take a different number of people and find a pattern, where n is the number of seats, and w (n) is the winner. ”
')


Consider what happens on the example of seven people: 1 kills 2. 3 kills 4, 5 kills 6. Well, but for 7 there is no 8, so 7 kills 1. Then 3 kills 5, 7 kills 3. 7 won.


This is Joseph, he wants to live.


Joseph in the detachment was 41 people. And this is serious.

Consider an example when there are 5 people in a group. 1 kills 2, 3 kills 4, 5 kills 1, 3 kills 5. The winner is 3.

For six. 1 kills 2, 3 kills 4, 5 kills 6, 1 kills 3, and 5 kills 1. The winner is 5.


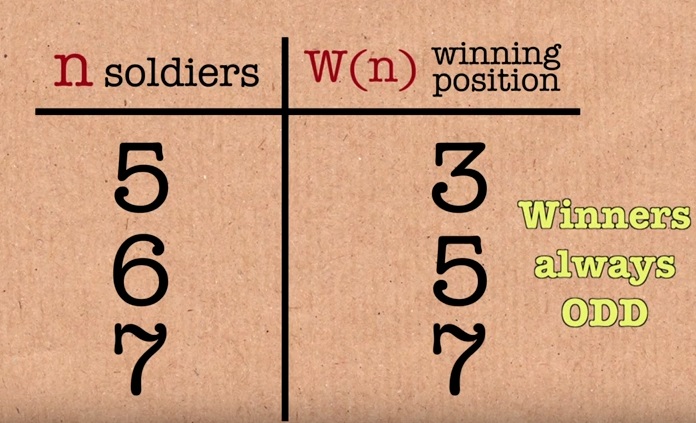
There are strange patterns. So far, the winner is an odd number.


Got to an even place - cranes.

Now complete the table.

Take one person. Well. This man won, so it was easy.

If there are two people: 1 kills 2. 1 - the winner.

If there are three people: 1 kills 2, 3 kills 1. 3 won.



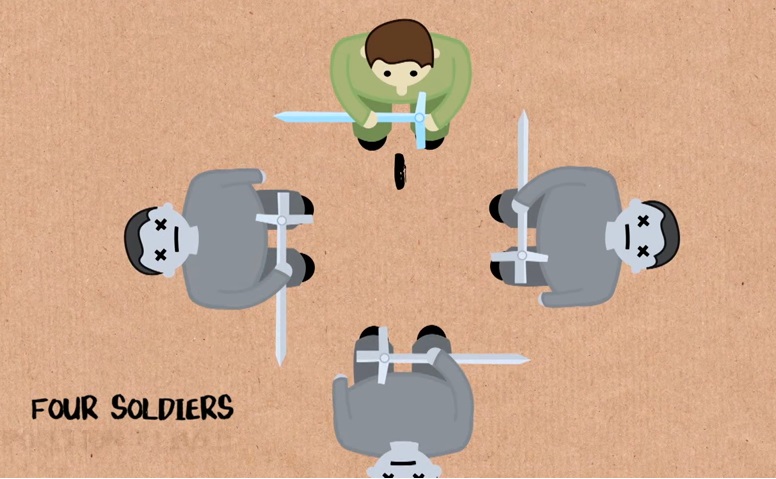
If there are four people: 1 kills 2, 3 kills 4, 1 kills 3.

If there are eight people: 1 kills 2, 3 kills 4, 5 kills 6, 7 kills 8, 1 kills 3, 5 kills 7, 1 kills 5. The winner becomes 1.

Well, the results are as follows: 1, 1, 3, 1, 3, 5, 7, 9.
The result all the time increases by 2, but then it is reset at some point.



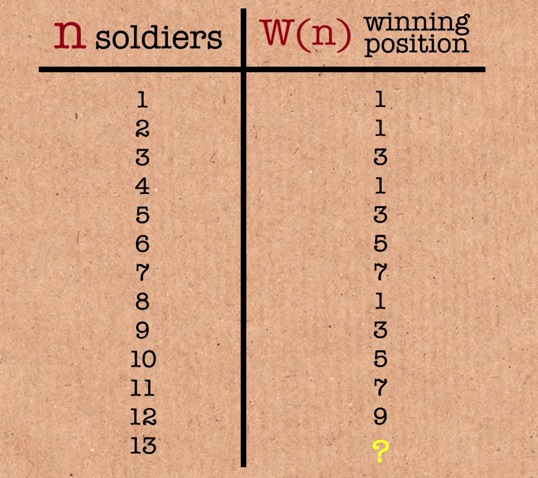
We'll do it quickly to 13, we get 11, and 14 will have 13.

Now let's see when a reset happens to one. Pay attention to the numbers that give you a unit. Already you can guess that the 16 winner will be 1.

We conclude:
If n (number of people) is 2 to the power, then the winning place is number one.

Now I will draw a bigger scheme. Scheme for 16 people.
After the first round of killings, half as many people will remain, that is 8. Now, again, we start with the first. We pass in a circle, and again half as much, that is, 4. We make another circle. There are two people left. We start with the number one, and he wins.

Now consider what happens to the numbers, between 4 and 8.

The result is increased by two. But, when I add 2 to 7, then it turns out 9. Here it happens and the reset to 1. And now I can say that, any combination can be written as 2 to the power plus some other number.



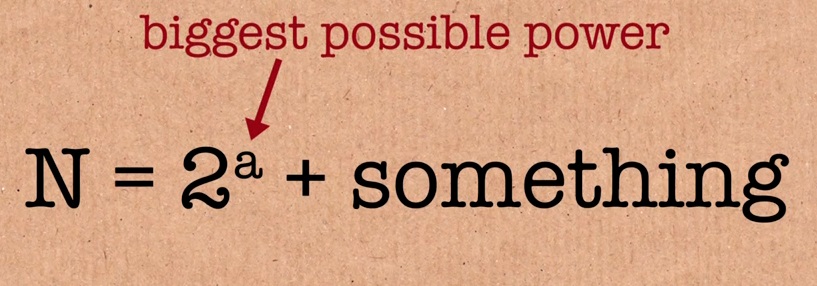
Take the number 77. The largest number from which I can extract the root is 64. Then we get the sum: 64 + 13.

Then we shall write out the largest roots of the same pattern for the number 13: 8 + 4 + 1. The sum of the twos in degrees is obtained. 77 = 2⁶ + 2³ + 2² + 2⁰. The key point is that the degrees do not repeat, so we did everything right.

And now we derive the formula, where 64 (n) is 2 to the power of A + 13 is L, we get n = 2ͣ + l

13 we write as the sum: 8 + 4 + 1 and substitute the formula n = 2ͣ + l (13 = 8 + 5)
And an odd number is the number of moves, after which you need to stop.
I will take five steps. So: 1 kills 2, 3 kills 4, 5 kills 6, 7 kills 8, 9 kills 10. I stopped at number 11. Now look what happens: how many people are left? What remains is the root of the two. And as we know, the one who wins at the root of the two is the one who starts!

Now we look: 11 kills 12, 13 kills 1, 3 kills 5, 7 kills 9. Again we come back to the eleventh, now only four people are left. 11 kills 13, 3 kills 7. There are 2 people left and the eleventh begins. The 11th won.

The theory is to paint a number using a formula where L is less than 2 to the power of a. And the winning place is 2L + 1.
Our last sum was 13 = 8 + 5, where 5 was L. We substitute in the formula and see that everything converges: 2 * 5 + 1 = 11

Let's return to our task. There were 41 people in the squad. 41 = 32 + 9
Take our formula 2L + 1. Get 19

Draw a circle.
So, 1 kills 2 ...
We lose our even numbers.
41 kills 1, 3 kills 5 ... 19 kills 35, 35 kills 1 and 19 kills 35.

The formula that I wrote can be painted in binary code. We write the sum of degrees: 41 = 2⁵ + 2³ + 2⁰. The code is nothing more than two to a degree. And the code is one or zero. Let us write in order of two in the degree on the left the largest at the end of two in degree 0. Where the degree corresponds to our value, then we set 1, otherwise - 0. Thus we get: 2⁵ 2⁴ 2³ 2² 2 2 2⁰. The binary code will be: 2⁵ - this is 1, 2⁴ - this is 0, etc. ... And we get: 101001.

And now I will show the main feature in solving the problem. The winning position will be your binary code, but the first digit needs to be moved back: 010011. It turns out: 2⁰ + 2¹ + (I missed 2² and 2³) + 2⁴. And here is the sum: 16 + 2 + 1, where the answer is 19.

That's all the solution for our problem.

PS

And in this position, Joseph did not abandon his prudence: in the hope of God's mercy, he decided to risk his life and said: “If it is decided to die, so let's give lots to decide who should kill whom. The one to whom the die falls will die at the hands of the one nearest him, and in this way we will all take turns in order to die one by one and avoid having to kill ourselves; Of course, it will be unfair if, after the others die, one will think and survive. ” With this proposal, he again regained their confidence; persuading others, he himself also participated in the draw. Each person who drew a lot, in turn, voluntarily gave himself to slaughter another companion who followed him, as soon after that the commander also had to die, and death together with Joseph seemed to them better than life. By a lucky chance, and maybe, by divine predestination, it was Joseph who was the last with one more. And since he did not want to be killed by the lot himself, or to stain his hands with the blood of his compatriot, he convinced the latter to surrender to the Romans and save his life. The Jewish War, book 3, chapter 8, 7

Read more

• Josephus Problem on the site of Wolfram
• Video lecture by Professor Steven Skiena
• Josephus problem on Wikipedia

About GoTo

• Competition GoTo Algorithms Challenge Spring 2018 (until March 21)
• Spring School GoTo 2018 (March 25-31)
• Group in VK
• Subscribe to the newsletter