Content

opening speech
Principle of operation
Program description
Final program code
Advantages of working with digitized functions with examples
Epilogue

---

opening speech

In various fields related to science and education, engineering encounters a task related to obtaining data from graphs created at the time when digital media did not exist, or real data for which graphs were created were lost, or, finally, the schedule is the final form of work of some devices that do not give a set of coordinates of points in an explicit form.

In order to get data, you need to “ digitize ” such a graph (or graphic object), in other words, you need to get a set of abscissas and ordinates of the graph points - then you can perform various manipulations on them: build a new (qualitative) graph, perform calculations, translating it into a new format (for example, building a spline), etc.
')
In the project " Tutor: Mathematics " (read the article on Habrahabr - "Tutor: Mathematics" to prepare for the EGE and CDF - from idea to release. A story about a unique educational project ) we met this problem in two main ways:

• “Digitizing” the graphics in order to make it fit our style or just make it look decent;
• obtaining a set of base points for constructing geometric drawings, histograms, etc., based on the author’s freehand drawing (or using simple graphic systems).

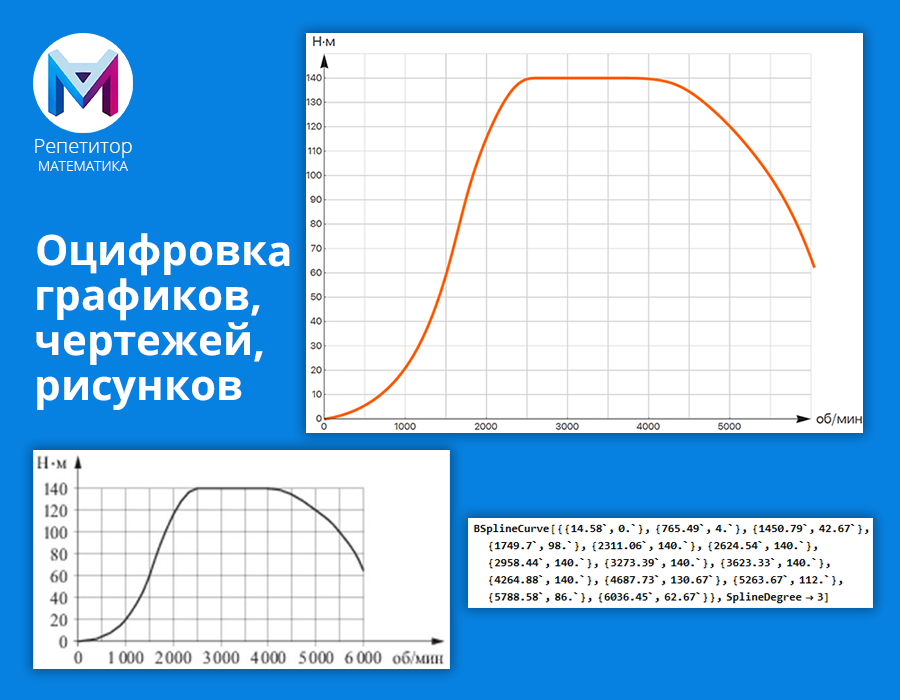
This post contains the code for the graphicsDigitizing function created for this, and also briefly describes how it works. You can also see how it works live .

Principle of operation

The work of the program is quite simple. It is necessary to put a digital illustration (scan, photo, screenshot, another picture) on some field on the “first” layer. Then it is processed manually:

• selection of the working area (rectangle) with the specification of the “real” coordinates of its left lower and right upper vertex - in other words, the domain of definition and the values ​​of that function (graph, set of points), which we get as a result;
• setting the control points on which the B-spline of a given degree will be built;
• preview the result;
• output of the result in a calculated form for further work.

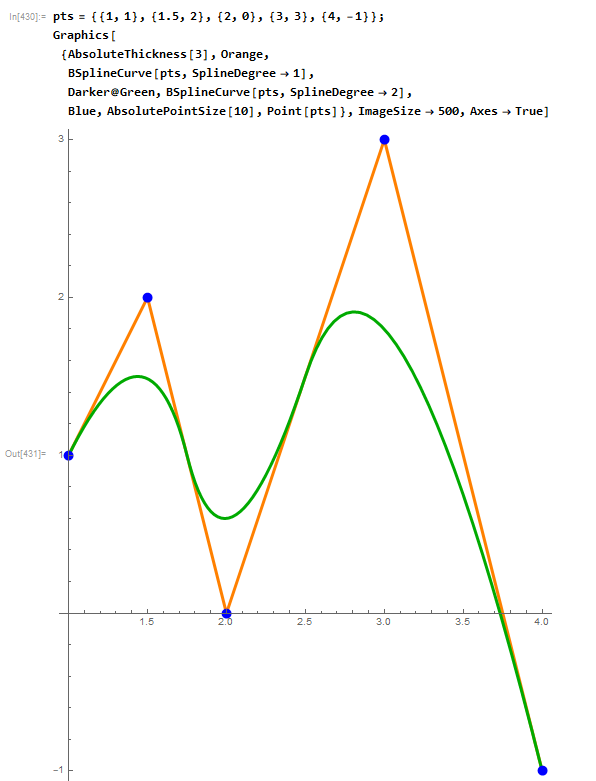
We chose B-splines for several reasons:

• they give flexible curves (if the degree of the B-spline is higher than 1st),
• give compact analytical representations of curves ( Bezier curves are a degenerate case of B-splines, in which each point, speaking simply, influences the whole look of the curve);
• they are easy to use (they are implemented in many packages and are not that complicated if you need to program them from scratch on your own).

The figure below shows a set of points (control points), a set of B-splines of the 1st, 2nd and 3rd degrees, as well as a Bezier curve (in the case shown, this is essentially a B-spline of the 7th degree).



To create a program for digitizing graphs - like for many other tasks - we use the Wolfram Language .

Program description

Of course, we will not describe how the entire code of the program presented below works in steps, it would be very long and, as it seems to us, those who are interested in the issue under consideration or, moreover, those whom he is acutely aware of will be able to understand in all the "cogs" of the code, good, it is short.

We will pay attention to its main elements.

Let's start with a set of functions that will be required for implementation. You can look at what each of them does in the documentation:

CompoundExpression , ClearAll , SetDelayed , Optional , Pattern , Blank , Image , ImageResize , List , Rule , ColorSpace , With , Set , ImageDimensions , CreateDialog , ExpressionCell , DynamicModule , Grid , DefaultButton , DialogReturn , If , Less , Length , None , Drop , Transpose , Part , Span , ReplaceAll , Rescale , All , Min , Max , RuleDelayed , Real , Round , CopyToClipboard , BSplineCurve , SplineDegree , TabView , Row , Slider , Dynamic , Times , Pi , Power , ImageSize , Small , Slider2D , SetterBar , InputField , FieldSize , Alignment , Left , Spacings , Automatic , LocatorPane , Framed , Graphics , Inset , Cos , Sin , EdgeForm , Directive , AbsoluteThickness , RGB Color , Opacity , Yellow , Rectangle , Dashed , Blue , PlotRange , Plus , LocatorAutoCreate , True , Center , Top , Axes , AspectRatio , Initialization , Null , Condition , String , FileExists , Import , BlankNullSequence , Echo , Inactive , Nothing

One of the main functions in the work of this program is the DynamicModule function for creating interactive spaces and objects. With its help, the "revival" of the whole structure occurs.

The Grid function is necessary for organizing space - it allows you to build tables of various shapes and place content in their cells: texts, sliders, illustrations, interactive objects, etc.

The LocatorPane , Slider , Slider2D , InputField functions are used to make interactive elements — a field with a selection of points, sliders (one- and two-dimensional, respectively), a text input field (for the function definition area).

To “draw” graphic primitives, use the Graphics function (and, if necessary in 3D, use Graphics3D ).

And, of course, the most important here is the BSplineCurve function, which allows you to represent a set of points as a finished B-spline curve.



In the video below you can see how the program works live:

Final program code

The final function is actually not as great as it might seem. Although this, of course, a direct consequence of the great opportunities Wolfram Language:

Advantages of working with digitized functions with examples

Naturally, with the graphics before digitizing, any work is extremely difficult, however, after you have digitized the schedule, say, with the help of our program, you can already do a lot. Let us show some examples.

For example, let the schedule be given:



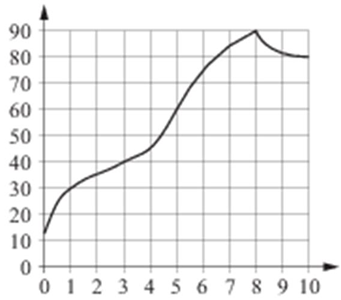
Let's digitize it (see video above ) and make calculations.

For a start, just replace the head part of the expression obtained during the operation of the program from BSplineCurve with BSplineFunction , which builds an analytical expression with which you can already perform calculations:



The only drawback is that such a function is normalized to 1, that is, the function f (t), when t is changed from 0 to 1, runs through all its values, which are B-spline points:



However, this is easy to deal with. It is enough to construct an interpolation polynomial:



After that, you can do anything.

Build a graph, say, from 1 to 9:



Integrate the function across the entire task area:



Build a graph of the derivative:



Find the length of the curve:



Or the analytical representation of the curve (in parametric form):



And you can, of course, simply improve the original schedule:

Epilogue

We hope that the story about the digitization function will be useful to you and you can use our algorithm. Ahead, as we promised in the previous article, you will find many more new stories about our application and algorithms that are under his hood.

---

An article of their series of articles on the project " Tutor: Mathematics " to prepare for the EGE and the CDF.