Effective data compression methods when training neural networks. Lecture in Yandex
Not so long ago, Gennady Pekhimenko, a professor at the University of Toronto and a PhD from Carnegie Mellon University, came to Yandex. He gave a lecture on coding algorithms that allow to bypass the problem of limited memory of a GPU when learning deep neural networks.
- I belong to several groups of the University of Toronto. One of them is Computer Systems and Networking Group. There is also my own group - EcoSystem Group. As can be seen from the names of the groups, I am not an expert directly in machine learning. But neural networks are now quite popular, and people who are engaged in computer architecture and networks, computer systems, have to deal with these applications on an ongoing basis. Therefore, the last one and a half or two years I have been closely involved in this topic.
I'll tell you how to properly do compression in memory, in the processor cache. This was the topic of my doctoral thesis in America at Carnegie Mellon. And it will help to understand what problems we encountered when we wanted to apply similar mechanisms for other applications, such as neural networks.
One of the main problems in computer architecture is that we want to get high-performance systems - graphics cards, coprocessors, phones, laptops - with good energy efficiency parameters.
')
At the moment, it is easy to get a fairly high performance, if you do not limit yourself to memory. You can get and exoflop computer, if necessary. The question is how much electricity you have to spend. Therefore, one of the main problems is to get good results on performance with the available resources and at the same time not to disturb the balance of energy efficiency.
One of the main problems in the path of energy efficiency is that many key applications used in cloud computing and on various mobile devices have significant data costs, both for shipping and storage. These include modern databases, graphic cards, and, of course, machine learning. All this requires very serious resources from all levels of the stack, from the core down to network resources.
Here is one of the key problems that arise when you have to perform various optimizations: you can actually replace one type of resource with another. In the past, in computing architecture, computing resources themselves, such as addition, multiplication, and arithmetic operations, were very expensive. However, this situation has changed in recent years, and this is due to the fact that the development of the processor core has progressed much faster than the speed of access to memory.

As a result, one arithmetic addition operation in terms of energy will cost you approximately 1 picojoule. In this case, a single floating point operation, floating point, will cost approximately 20 pj. If you want to read 4 or 8 bytes from memory, it will cost you at least two orders of magnitude more in energy. And this is a significant problem. Any attempt to work with memory is quite expensive. And it doesn’t matter what devices we are talking about. The situation is the same for mobile phones, that for large clusters and supercomputers.
It follows from this that very many resources that even the current mobile phone does not have can be fully utilized for energy resources. If you take a modern phone, it does not matter, Android or iPhone, we can use the available bandwidth between memory and the core in peak and only by about 50%. If we do not do this, the phone will overheat, or rather, no one will overheat to it - the bus frequency will be reduced when communicating between the memory and the core, and the performance will also fall.
Many resources are now impossible to use if you do not apply clever optimization.
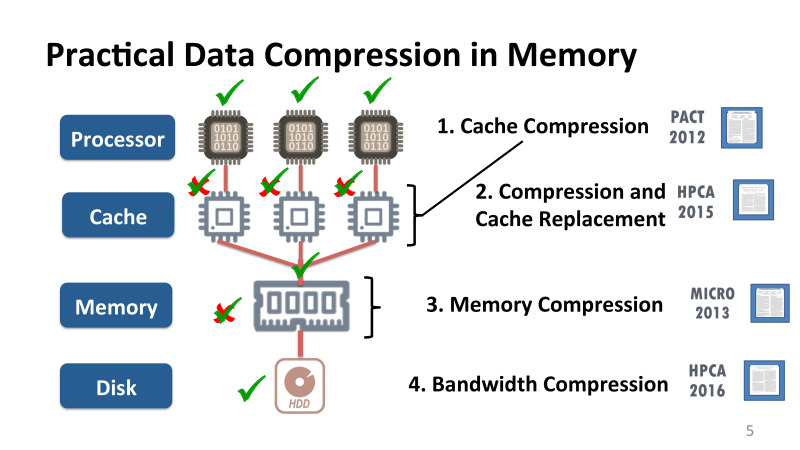
One way to deal with the lack of different resources at different levels is data compression. This is not a new optimization, it has been successfully applied both to networks and to disks, we all used various utilities. Say, on Linux, many have used gzip or bzip2 utilities. All these utilities have been very successfully applied at this level. Algorithms are usually applied either on the basis of Huffman encoding or Lempel-Ziv.
All of these algorithms usually require a large vocabulary, and the problem is that their algorithms are very consistent, and do not really fall on modern architecture, which is very parallel. If we look at existing hardware, memory-level, cache, or processor-level compression has hardly ever been applied, at least until some of our first jobs five years ago.
I will tell why this happened, and what can be done to make compression available at various levels, that is, compression directly in the cache. Cache compression - meaning that the compression takes place directly in the hardware, that is, a part of the logic of the processor cache itself is changing. Briefly tell you what this bonuses. I'll tell you about the compression in memory, what problems are there. It seems that this is the same thing, but to effectively implement compression in memory is quite different, not the same as in the cache. I'll tell you about the collaboration with NVidia, where we made Bandwidth Compression in real hardware for modern GPUs, and the optimization that we did is in the latest generation of GPU cards - Volt. And I’ll tell you about a completely radical optimization, when execution takes place directly on compressed data without decompression at all.
A few words about the compression in the cache. This was an article at the PACT conference in 2012, and the work was done in conjunction with Intel. To make it clear what the main problem is, if you want to turn your 2 MB or 4 MB processor cache into 4 MB or 8 MB. You did L-compression, and what's the problem?
Roughly speaking, when you have a memory access operation, if we are talking about the x86 architecture, load or store in memory, then if there is no data on the registers, then we go to the first level cache. Usually it is three or four clock cycles on a modern processor. If the data is there, they go back to the CPU. If they are not there, then the request to memory goes further along the hierarchy, comes to the L2 cache.
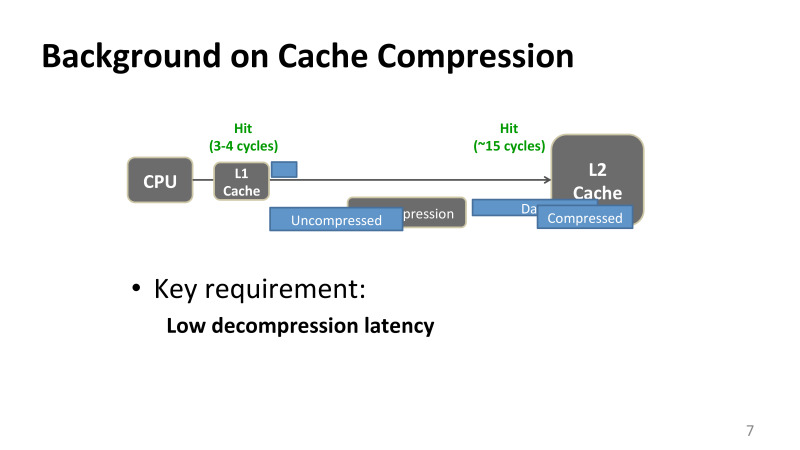
L2-cache on most Intel processors 15-20 cycles, depending on the size of the cache. And then the data usually go back, if they were found in the L2 cache, if you did not go to the memory. The data goes both to the processor immediately and to the L1 cache, if you continue to reuse this data so that they are closer to the processor.
The problem is that if the data is compressed, then it doesn't matter how you optimize the compression process, decompression is always on the critical launch path. If earlier a second level cache call took 15 cycles, then any delay associated with decompression is added to the delay of your request. And this restriction is true for almost all applications of compression, and in memory, and when we use for real-world applications, such as training neural networks, decompression is always on a critical path, and its delays, the time for its execution is very critical.
What does this mean for us? If you understand that the cache latency is at 15 cycles, decompression should be very optimized. We can afford only a few processor cycles. To understand how small it is, one plus takes about two cycles, one such simple operation. That is, you can not do anything super complex.
Largely because of this, Intel at some point focused on developing cache compression. They had a whole group that worked there, and in 2005-2006 they developed an algorithm that gave decompression of about 5 cycles. This delay increased by approximately 30%, but the cache became almost twice as large. Nevertheless, their designers looked at most applications and said it was too expensive.
When I started working on this topic in 2011, they said that if you can do something in 1–2 cycles, you can do it in real hardware, try it.
I tried different algorithms, and one of the reasons why it was not possible to use the algorithms that already existed in the literature is that they were all made originally in the software. In the software, other restrictions, people use different dictionaries and other similar techniques. If these techniques try to do in real hardware, they are quite slow. IBM made the Lempel-Ziv algorithm completely the same as in gzip used, completely in hardware, and decompression took 64 clocks. Clearly, in the cache you will not use this, only in memory.
I tried to change the strategy. Instead of trying to optimize software algorithms, I decided to see what kind of data is actually stored in the cache, and try to make an algorithm that will work well for this data.

I saw that paradoxically a lot of zeros, from 20% to 30%. If you take a large package of applications from Intel, there are 200 different applications that people use for computing - there are a lot of zeros. This is initialization, these are matrices with a large number of zeros, these are null pointers. There are many reasons for this.
Very often there are duplicate values. In some small area of memory, in the cache, very similar values can be repeated. This, for example, and if you work with graphics, you have a bunch of pixels, and if you have a part of a picture with the same colors, then you have all the pixels that are in a row going to be the same. In addition, narrow values, single-byte and two-byte values, which are stored in 2, 4 and 8 bytes. Why is this happening and whose error is this? Where does such redundancy come from?
Redundancy is related to how we program the code. We use some language, for example, C ++. If we want to allocate memory for some object, say, for a whole array, imagine that in the array we store statistics about some events, and these events can be both very frequent, say, billions, and single. For example, reference to memory with a specific instruction. Most instructions are not memorized, but some can be accessed billions of times during startup.
The programmer is forced to allocate an array of eight-byte numbers, because in the worst case, his integer values can take large values. However, this is redundant. Many of these values are not really needed, and there will be a bunch of incomplete zeros, but some of the leading zeros.
In addition, we have many other values that also have different types of redundancy. For example, pointers. Anyone who once debugged the code and looked at the pointers, you can see that they are changing quite large. But if you have pointers with approximately one memory area, then most of the bits ahead will be the same. This type of redundancy is also evident.
I have seen many types of redundancy. The first question is how many are there?
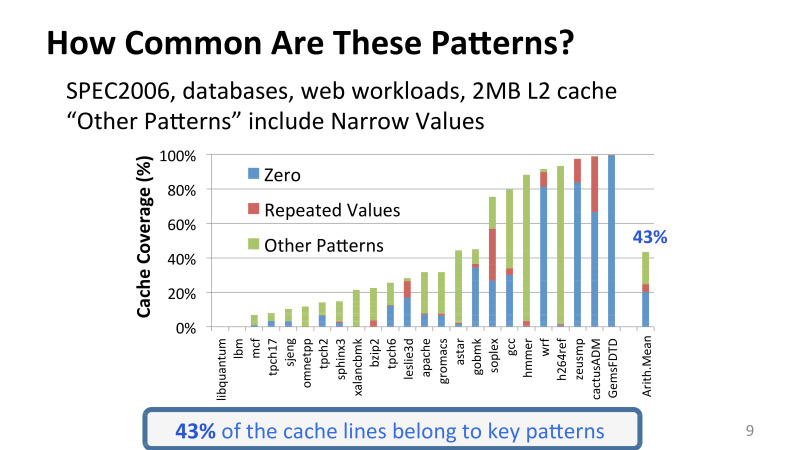
Here, the experiment in which I periodically took data from the second-level cache saved the snapshot of this cache and watched how many zeros there were, repeated values. On the X axis, various applications from the SPEC2006 package, which is actively used in the computer architecture, as well as other various applications from Intel, include both the database and various web workflows, such as the Apachi server, for example. And here is the assumption that this is a 2 megabyte L2 cache.
You may notice that there is a large variation between redundancy in different applications, but even these very simple patterns are quite common. Only they cover 43% of all cache lines, all data that is stored in the cache.
You can come up with something quite simple that will cover these and maybe some other patterns, and give us good compression performance.
However, the question is, what makes these patterns related? Will I have to do some kind of compression algorithm that will work specifically for each of these patterns, or can I do something in common?
The general was the idea of observation. All these values, they can be both large and small, there is very little difference between them. Roughly speaking, the dynamic range of values in each specific cache line is very small. And you can imagine the values stored in the cache, for example, the 32-byte cache line can be represented simply using Base + Delta Encoding.
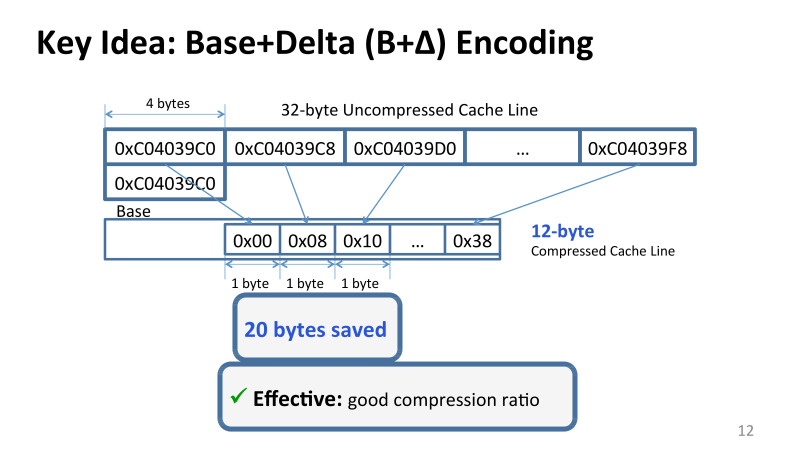
Take, for example, the first value for the base, and all the others as an offset from this base. And since the values from each other differ in most cases not much, then our delta fits in one byte, and instead of 32 or 64 bytes we can do with only 12 bytes and save about 20 bytes of space.
I will not talk about all the details of how to implement it in real hardware. We made a real prototype, wrote a prototype on Verilog, drove it on modern FPGAs, talked to Intel about implementation. You can make an algorithm based on this idea, which will require only one or two clocks in decompression. This algorithm is applicable, and it gives a good compression ...
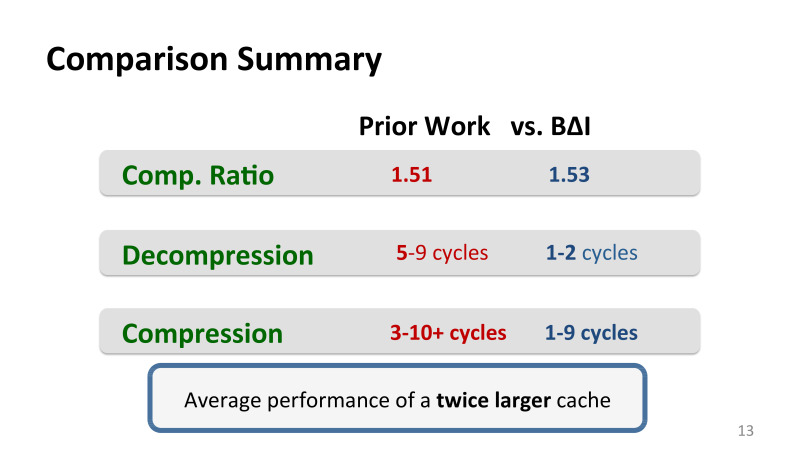
The best previous works that were used in the cache, gave about 50% of additional space. This is not a pure compression - it can give a lot more - this is a real bonus to effective compression, that is, how much cache looks to users. There are still any problems with fragmentation and so on that need to be addressed.
Compression is at the level of the best previous mechanisms that Intel had, but the main gain in the middle of the slide is decompression. The previous algorithms, they had the best decompression was 5-9 cycles. We managed to do it in 1-2 clocks, while the compression is also quite effective.
Algorithms of this kind can be done in real hardware and applied in the cache, for example, in memory.
The effect of applying such optimization in the cache leads to the fact that the cache looks to the user often almost twice as much in efficiency. What does it mean? If you look at the modern processor, in the photos, there are almost no cores themselves. There, most of the space is occupied by processor caches - 40-50% easily from both IBM and Intel. In fact, Intel can not just take and double the cache, there is simply no room for more cache. And such optimizations that cost only a few percent of the core itself are, of course, very interesting.
We worked with various optimizations in the second work, which I will not talk about today, about how to work with such caches, which now can have different cache line sizes. All these problems have been successfully resolved.
I want to talk about our third work, which was also done with Intel, about how to compress memory.
What problems are there?
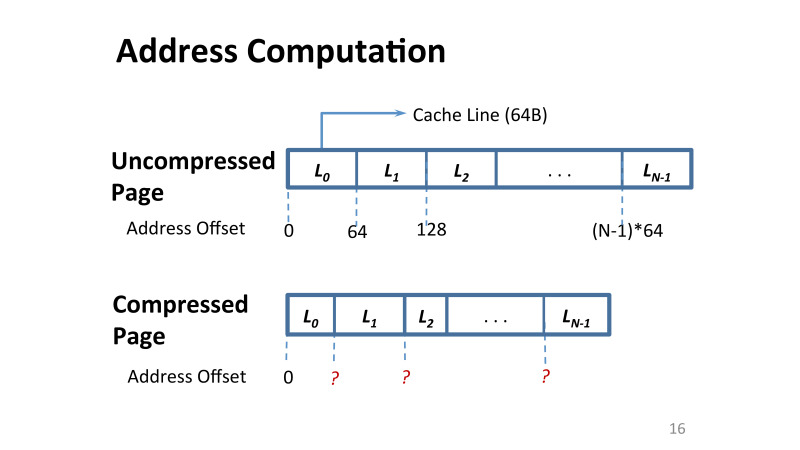
The main problem is that if in Linux or Windows I have a 4 KB memory page, then in order to compress it, I need to solve the following problem: I need to solve the problem of how the data addresses on this page change. Initially, you have 4 KB, and each cache line in it is also 64 bytes. And the offset of any cache line inside this memory page is trivial to find: you take 64 and multiply by the offset you need.
However, if you use compression, each line is now potentially of a different size. And if you need to read some page from the memory now, you do not have these displacements.
We can say that you can save them somewhere. And where to keep them? Either again in memory or in cache. But if you want to save all offsets for each memory, you don’t have enough cache, you need resources of the order of hundreds of MB to serve all the memory. You cannot save this data in the chip, and you don’t want to store it in memory, because each memory access will now be several memory accesses. First you will go for the metadata, and then for the real data.
The second problem that everyone faced when working with the OS is data fragmentation. Here it becomes extremely complex, because each page also occupies a different place in memory. At the same time, in the virtual address space all pages are still 4 Kb, but after compression they all occupy completely different sizes. And this is a problem, how now to work with this empty place. The OS is not aware that we have allowed the pages to be made smaller, it just does not see these fragmented pieces. Just like that, without changing anything, we will not receive bonuses from compression.
What did we suggest to solve this problem? Compression using a linear coefficient. We imposed a set of certain restrictions, which are described in detail in the article, but the bottom line is that if I apply compression to memory, I use an algorithm that ensures that every cache line on this page either compresses with a certain factor, say, 4 to 1, 3 to 1 or not compressed at all.
We potentially lose something in terms of data compression, because we impose additional restrictions, but the main bonus is that the design is very simple, it can be implemented, which we have successfully done, for example, in Linux.
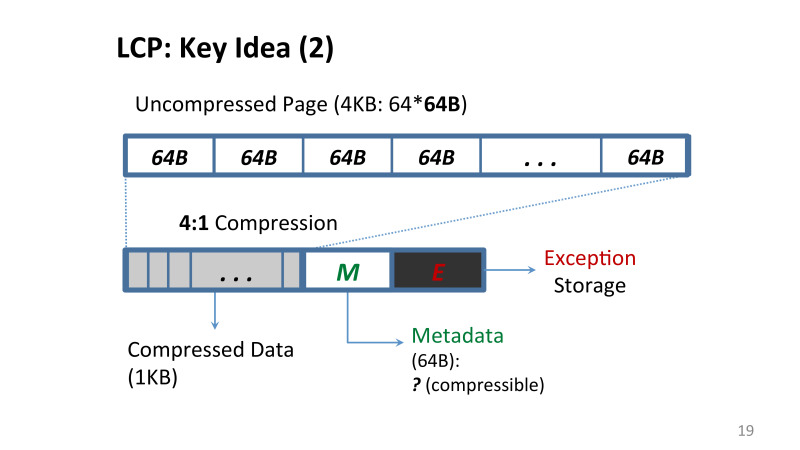
Linearly Compressed Pages (LCP), a technique that we proposed, copes with the main problem that now the addresses of all the data are quite simple. We have a small block of metadata that is stored on the same page, and there are either original data that is stored in a compressed form, or the so-called exception storage, cache lines are stored there, which we could not compress in this way.
Based on these ideas, we managed to get good data compression, and most importantly, I compare it with the best previous works that were made mainly by IBM, they also had good algorithms for compression.
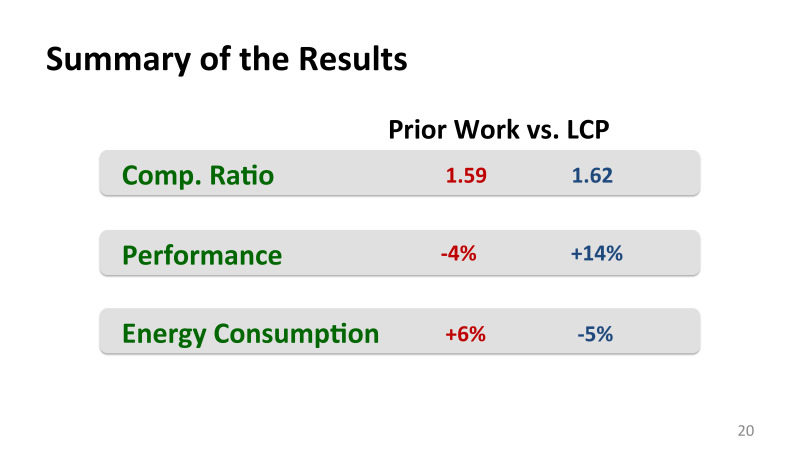
Our compression was not particularly better than theirs, but most importantly, we got more memory without paying extra performance for it. Roughly speaking, they got more memory, but for this they had a loss of performance, albeit small, but there was. . , , .
, . Nvidia. . , , 5-6 . bandwidth, .
, Nvidia, 2014 , , , . , : , DVFS, , , , , , , .
— , , . , , . . , - , , , . Nvidia , .
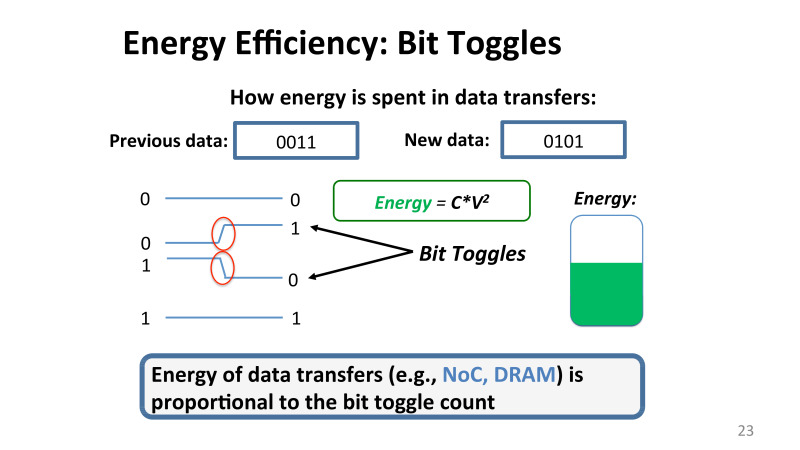
, , . . , , , 0011. . 0101. , 0 0, , bit toggle, , , , , , 0 1 1 0. , . , . , .
— , . , , networks of chip DRM , , .
What is going on? ?
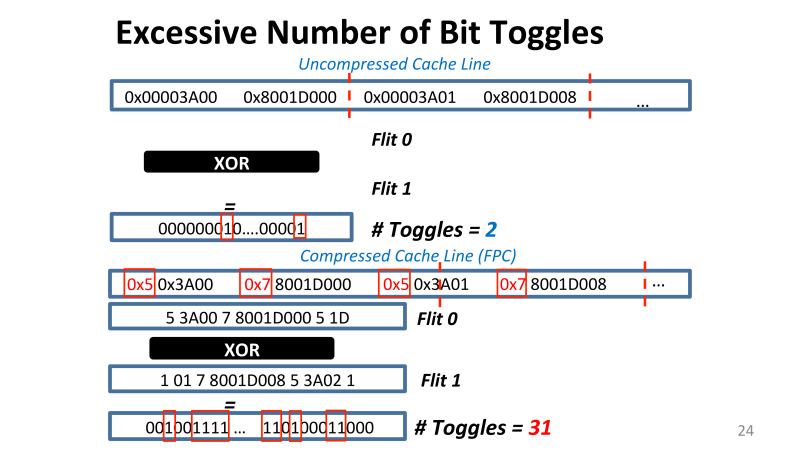
Nvidia, . , 32 16 , . ? , . , , XOR, 16 8 , , .
- , , frequent pattern compression, Intel, , . 15, 16 . , , , alignment. , . , . , Nvidia . , , , , . , 2%, 40%. , .
, . , , , , , , , , , , .

. , , , . , , , - , — , . , , . , , , , , .
, , , Microsoft Research , machine learning.
, , , , . DNNs. . , DNNs — , - Ajura, , , , . , 10%. , , , : TensorFlow, CNTK, MXNet. , , .
DNNs , , , GPU.
DNNs . , , , , . . , , , , . , .
, . , , inference.
, Google TPU , , , inferent , , Microsoft.
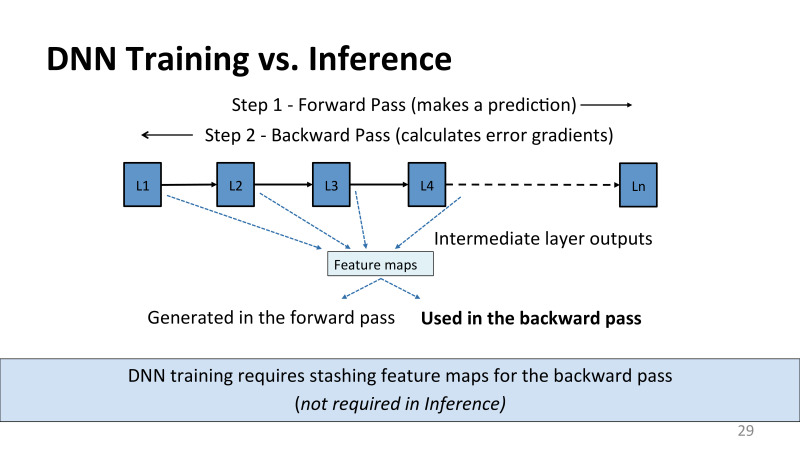
? ? Google, , TPU inference. , . , inference, . forward pass. , - , inference . — . , . backward pass, , , .
, , . , . , , feature maps activations. inference , . back propagation, , , , . , L2, , forward pass , , , , .
, , 100, 200 , , ResNet, image classification. - . — , , ResNet 101 , , , - mini batch , , 64 , , , 16 . , P100 Pascal Volt100, 16 . , .
, Facebook, . , , , . , .
, . GPU, . , .
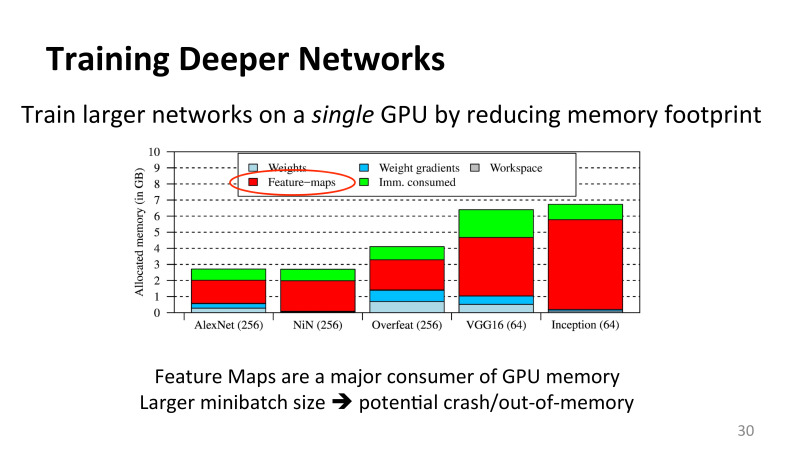
, , , , , . X AlexNet, DNN , : Overfeat, VGG16, Inception ( Google version 3, , Google). mini batch. , , . , , ImageNet, 220 220 3, 1000 : , , .
? AlexNet , 2011 , . , , feature maps, .
? , , mini batch, , , inputs. ? GPU . GPU 8000 threads, , , GPU . , ? , CPU ISAC.
, . , . , , , , , , , DNN inference, , ISCA, MICRO, 2015 15 , deep neural networks, inference, .
-, inference, , forward pass, , , .
, , . , inference, - , , 32- floating point, , 16 , 8 4. , , - stochastic gradient descend, . , . GPU, ISAC, - TPU - FPGA . GPU .
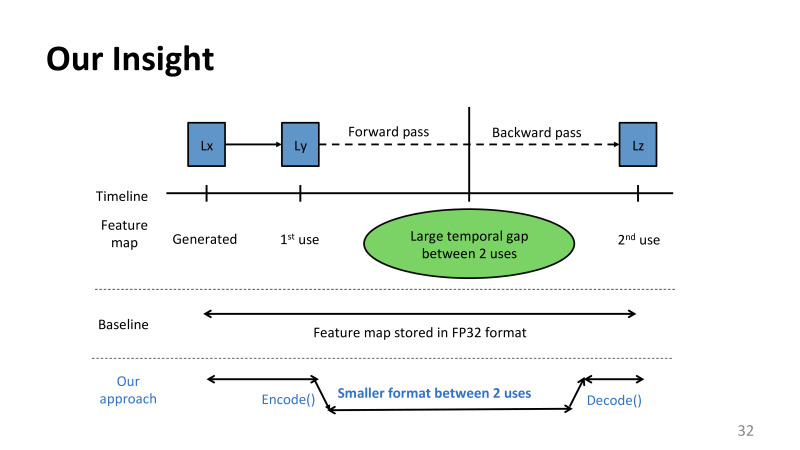
, . , , , , , , , , , , , LX, . , , . . : .
, . - , . , . . . , . , . , . .
, , ? , . , , . , , , . , . - , .
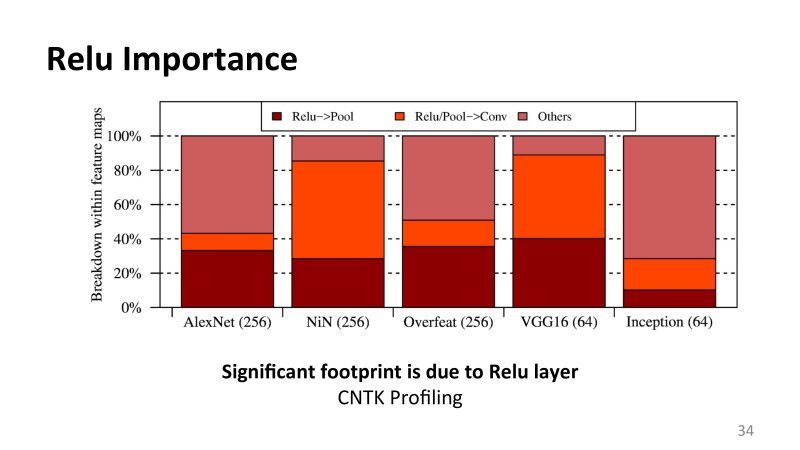
, , : feature maps . , , , , . , , , Relu , rectified linear function pulling layer, , , .
, , . , . , , , Relu, pulling layer. layers, .
, Relu , , - — . — .
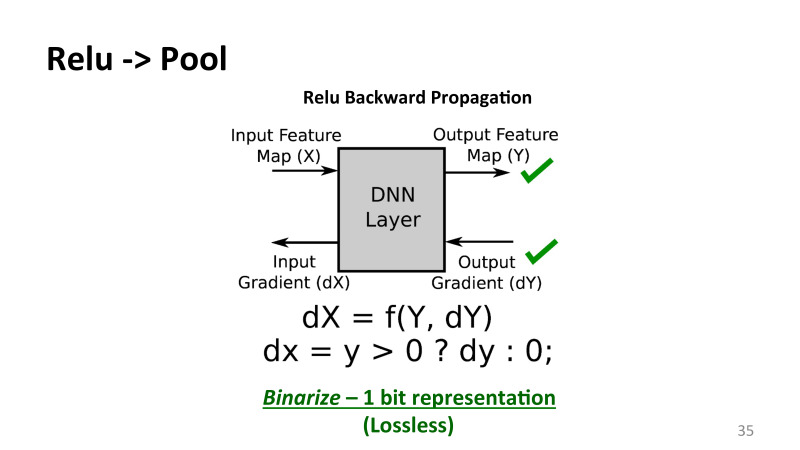
, Relu, . , . Relu — , , , 0, . — , , .
, , , by modal. . , , . , , . - , 32 , , , 31 . , , .
32 , . . , . , pulling layer — 2 2, , 2 2 3 3. , , , . TensorFlow, CNTK, , , . , , machine learning, , . . , , , - , , .
- , , , , . Relu 32 , pulling layer 8 . , , TensorFlow, . - . .
, 32 1 . , , . , . 32-, , . .
, lossless, .
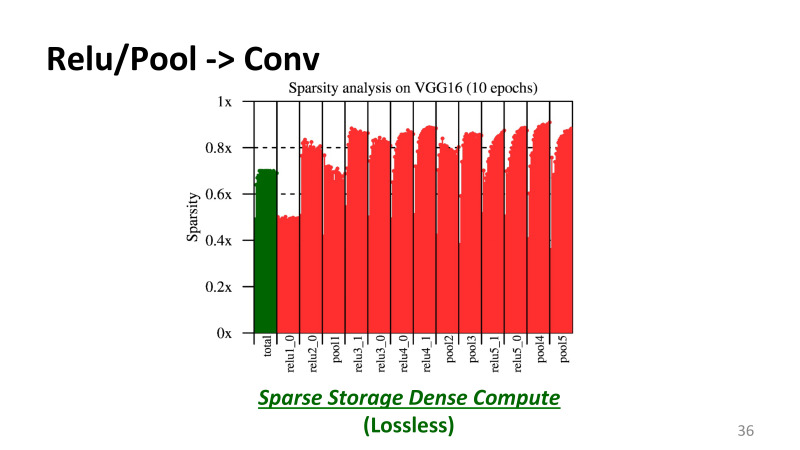
, Relu . . , , VGG16, 10 , , — , . 1 100% , 0,6 — 60% . , .
, , Relu_1, Relu_2 , . , , 60%, 70%. , , , . , .
What does it mean? , . , , GPU. CUDA , . , - CUDA . , NVidia , 99%. . , 50% 80% . , GPU . , , , CUDNN , Nvidia . , CUDA , .
, , , Lossy Encoding, . , IBM . , L1 - . 32 , 8 16, - , .
, 32- 16- , , , , , , AlexNet, 32 16 - , , , , validation. , , . , , , . , , , .
. , , , . , , . — . forward pass . , , backward pass, . backward pass, .
?
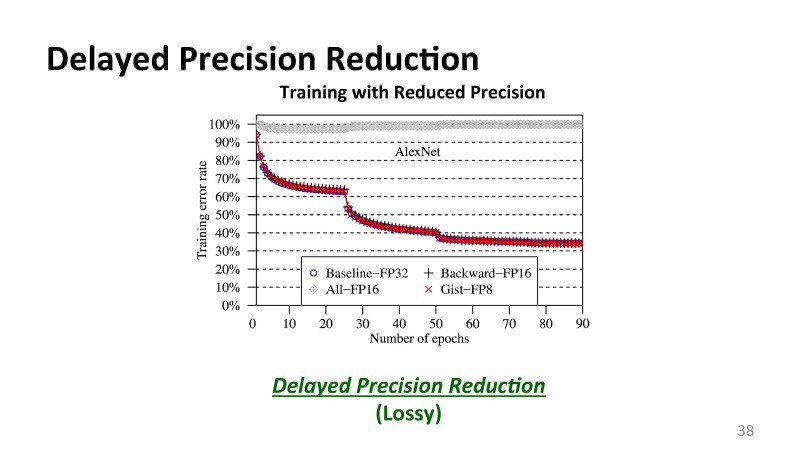
, . — AlexNet FP32, 32 . , IBM , All-FP16, 16 , . - 16 , , 16 , , , - .
, , , , 16 , 8 . , .
, , . , , .
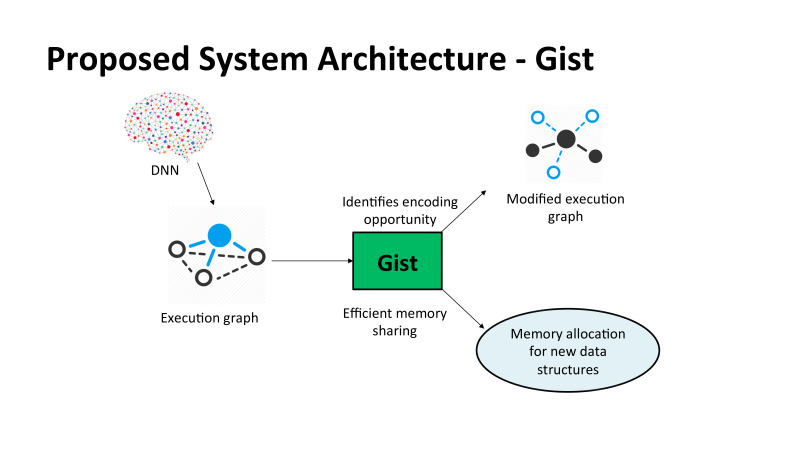
, Gist, «». DNN, execution graph, , , , CNTK , Microsoft. CUDA . execution graph, , TensorFlow, MXNet, . GPU , , . , , .
, , , cuDNN, , . . . , TensorFlow. GIST .
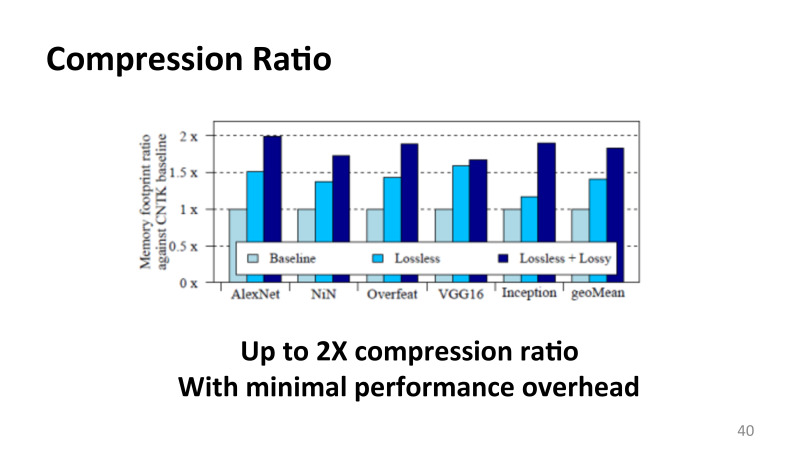
, , ? . , , , , , , 90-100 , . . , , . 6% 8%, , , , . , , Microsoft.
, . , , Microsoft, PhD , , DNN Training, , , , , . . Microsoft , LSTM , speech , , . - -, .
. , , . image classification, AlexNet, ResNet , . Image classification — , , , Facebook. , machine learning .
, , , . , . , MXNet, Amazon, , , TensorFlow. ResNet 50, , «» , 40% , TensorFlow . , MXNet , TensorFlow? . . LSTM, MXNet , TensorFlow, - , Amazon Google, TensorFlow 2,5 . , . .
, . , . , , , , machine learning, .
, , Image Classification, , . object detection, , , Faster RCNNs, 16-17- Google MIT, . : LSTM, , , . nmt — Google, open source. sockeye Amazon. .
Transformer, Attention layers. 2013-, , , , , Attention layers. Google , GPU, , .
speech recognition, LSTM. adversarial networks, reinforcement learning, Google AlphaGo . supervise, n-supervise learning. image classification. , . 16-17- , .
, . TensorFlow, CNTK, MXNet. , , , . TensorFlow , - CNTK MXNet. , , , . , , .
. GPU. , CPU . , , GPU, FPGA, ISAC Google. , TensorFlow, .
: , , , , -. .
, , , , . , , , CNTK. . , . TensorFlow , , 2000 , , , , . . , CNTK, MXNet. TensorFlow , . , Google … , , , , , .
, .
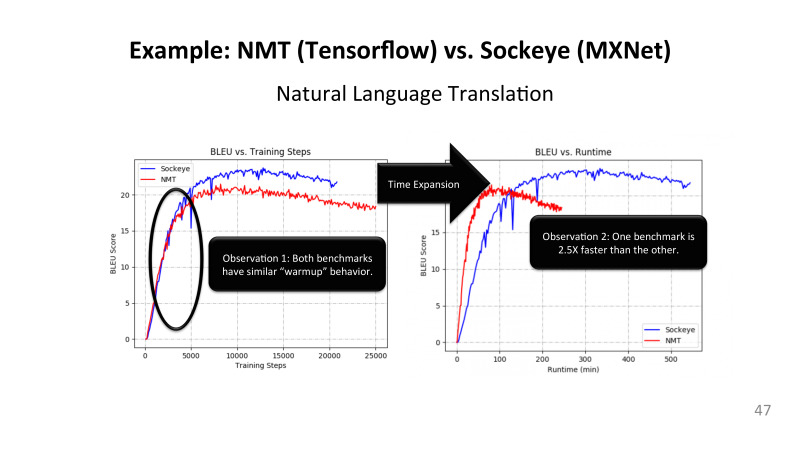
, TensorFlow MXNet . , NMT Google, Sockeye. , - , LSTM , batch, , .
, , , -, Y blue score. , , . , . .
? , , , blue score 20 . , , . SGD. , , - , .
- , learning rate , -, . . , , , , , , . , TensorFlow LSTM . CUDNN, MXNet LSTM. , .
, , TensorFlow, MXNet. , GPU, LSTM , 30% GPU . 70% . , , . TensorFlow 10-15%, . , MXNet. .
LSTM, , Nvidia CUDNN , LSTM . , . -, E , , CUDNN 2,5 LSTM. , «» P100 CUDNN 8 , «» 100 CUDNN 9 . . , . .
reinforcement learning, . , NIPS ICLR, . , machine learning MATLAB . , , . , , , . . Google, , .
, - , . .
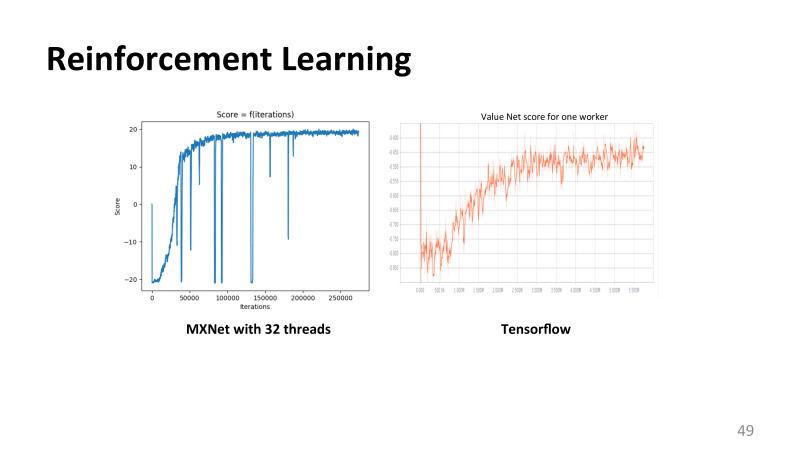
reinforcement learning, MXNet TensorFlow, , .
, . , , , , , , . , , .
, , : , . What does it mean? , , . , - , , . , . , Google , 5-7%.
cloud tax 20–25%, , , . , Google Cloud, 25% — , .
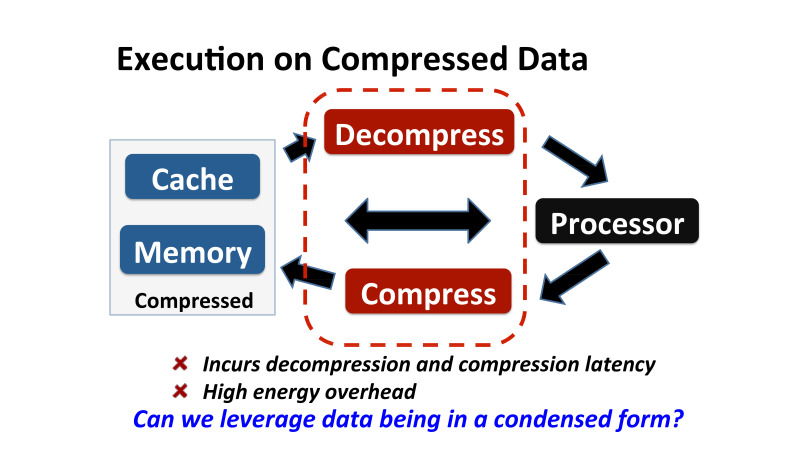
— . , - , ? , , , .
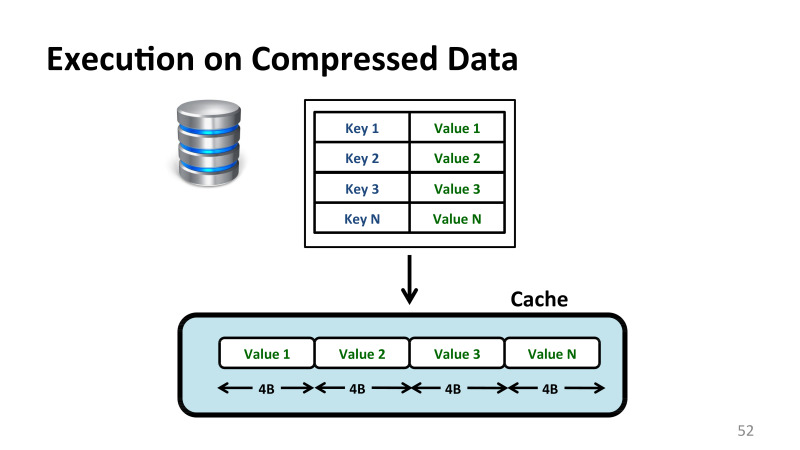
, . . , -, - . - , - . . , , , . , where value = 10, value . , .
, 4 .
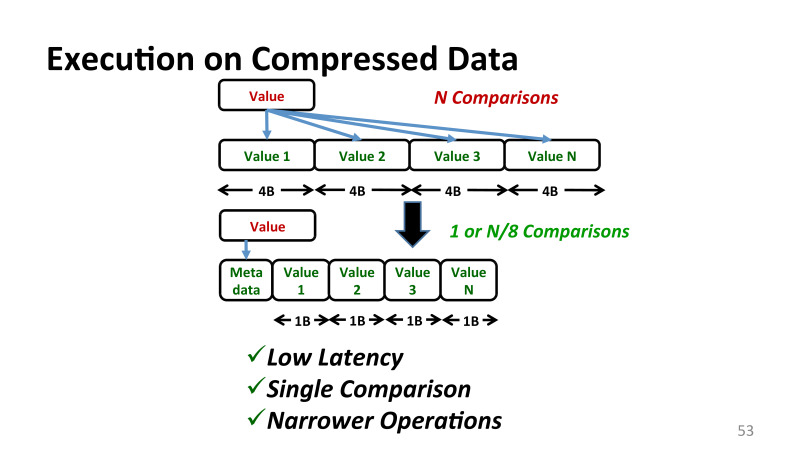
, , , Base+Delta Encoding, - . , 1 , . .
, -. , , ? - , , . , , - , n . , , , . , Base+Delta Encoding . , , Base+Delta Encoding.
What does it mean? , , . .
, , , , , , .
, 1 — , . , , — . , . . , CND- Intel . , 1 , . 4 8 .
, . . , , . , . It's all.
- I belong to several groups of the University of Toronto. One of them is Computer Systems and Networking Group. There is also my own group - EcoSystem Group. As can be seen from the names of the groups, I am not an expert directly in machine learning. But neural networks are now quite popular, and people who are engaged in computer architecture and networks, computer systems, have to deal with these applications on an ongoing basis. Therefore, the last one and a half or two years I have been closely involved in this topic.
I'll tell you how to properly do compression in memory, in the processor cache. This was the topic of my doctoral thesis in America at Carnegie Mellon. And it will help to understand what problems we encountered when we wanted to apply similar mechanisms for other applications, such as neural networks.
One of the main problems in computer architecture is that we want to get high-performance systems - graphics cards, coprocessors, phones, laptops - with good energy efficiency parameters.
')
At the moment, it is easy to get a fairly high performance, if you do not limit yourself to memory. You can get and exoflop computer, if necessary. The question is how much electricity you have to spend. Therefore, one of the main problems is to get good results on performance with the available resources and at the same time not to disturb the balance of energy efficiency.
One of the main problems in the path of energy efficiency is that many key applications used in cloud computing and on various mobile devices have significant data costs, both for shipping and storage. These include modern databases, graphic cards, and, of course, machine learning. All this requires very serious resources from all levels of the stack, from the core down to network resources.
Here is one of the key problems that arise when you have to perform various optimizations: you can actually replace one type of resource with another. In the past, in computing architecture, computing resources themselves, such as addition, multiplication, and arithmetic operations, were very expensive. However, this situation has changed in recent years, and this is due to the fact that the development of the processor core has progressed much faster than the speed of access to memory.

As a result, one arithmetic addition operation in terms of energy will cost you approximately 1 picojoule. In this case, a single floating point operation, floating point, will cost approximately 20 pj. If you want to read 4 or 8 bytes from memory, it will cost you at least two orders of magnitude more in energy. And this is a significant problem. Any attempt to work with memory is quite expensive. And it doesn’t matter what devices we are talking about. The situation is the same for mobile phones, that for large clusters and supercomputers.
It follows from this that very many resources that even the current mobile phone does not have can be fully utilized for energy resources. If you take a modern phone, it does not matter, Android or iPhone, we can use the available bandwidth between memory and the core in peak and only by about 50%. If we do not do this, the phone will overheat, or rather, no one will overheat to it - the bus frequency will be reduced when communicating between the memory and the core, and the performance will also fall.
Many resources are now impossible to use if you do not apply clever optimization.

One way to deal with the lack of different resources at different levels is data compression. This is not a new optimization, it has been successfully applied both to networks and to disks, we all used various utilities. Say, on Linux, many have used gzip or bzip2 utilities. All these utilities have been very successfully applied at this level. Algorithms are usually applied either on the basis of Huffman encoding or Lempel-Ziv.
All of these algorithms usually require a large vocabulary, and the problem is that their algorithms are very consistent, and do not really fall on modern architecture, which is very parallel. If we look at existing hardware, memory-level, cache, or processor-level compression has hardly ever been applied, at least until some of our first jobs five years ago.
I will tell why this happened, and what can be done to make compression available at various levels, that is, compression directly in the cache. Cache compression - meaning that the compression takes place directly in the hardware, that is, a part of the logic of the processor cache itself is changing. Briefly tell you what this bonuses. I'll tell you about the compression in memory, what problems are there. It seems that this is the same thing, but to effectively implement compression in memory is quite different, not the same as in the cache. I'll tell you about the collaboration with NVidia, where we made Bandwidth Compression in real hardware for modern GPUs, and the optimization that we did is in the latest generation of GPU cards - Volt. And I’ll tell you about a completely radical optimization, when execution takes place directly on compressed data without decompression at all.
A few words about the compression in the cache. This was an article at the PACT conference in 2012, and the work was done in conjunction with Intel. To make it clear what the main problem is, if you want to turn your 2 MB or 4 MB processor cache into 4 MB or 8 MB. You did L-compression, and what's the problem?
Roughly speaking, when you have a memory access operation, if we are talking about the x86 architecture, load or store in memory, then if there is no data on the registers, then we go to the first level cache. Usually it is three or four clock cycles on a modern processor. If the data is there, they go back to the CPU. If they are not there, then the request to memory goes further along the hierarchy, comes to the L2 cache.

L2-cache on most Intel processors 15-20 cycles, depending on the size of the cache. And then the data usually go back, if they were found in the L2 cache, if you did not go to the memory. The data goes both to the processor immediately and to the L1 cache, if you continue to reuse this data so that they are closer to the processor.
The problem is that if the data is compressed, then it doesn't matter how you optimize the compression process, decompression is always on the critical launch path. If earlier a second level cache call took 15 cycles, then any delay associated with decompression is added to the delay of your request. And this restriction is true for almost all applications of compression, and in memory, and when we use for real-world applications, such as training neural networks, decompression is always on a critical path, and its delays, the time for its execution is very critical.
What does this mean for us? If you understand that the cache latency is at 15 cycles, decompression should be very optimized. We can afford only a few processor cycles. To understand how small it is, one plus takes about two cycles, one such simple operation. That is, you can not do anything super complex.
Largely because of this, Intel at some point focused on developing cache compression. They had a whole group that worked there, and in 2005-2006 they developed an algorithm that gave decompression of about 5 cycles. This delay increased by approximately 30%, but the cache became almost twice as large. Nevertheless, their designers looked at most applications and said it was too expensive.
When I started working on this topic in 2011, they said that if you can do something in 1–2 cycles, you can do it in real hardware, try it.
I tried different algorithms, and one of the reasons why it was not possible to use the algorithms that already existed in the literature is that they were all made originally in the software. In the software, other restrictions, people use different dictionaries and other similar techniques. If these techniques try to do in real hardware, they are quite slow. IBM made the Lempel-Ziv algorithm completely the same as in gzip used, completely in hardware, and decompression took 64 clocks. Clearly, in the cache you will not use this, only in memory.
I tried to change the strategy. Instead of trying to optimize software algorithms, I decided to see what kind of data is actually stored in the cache, and try to make an algorithm that will work well for this data.

I saw that paradoxically a lot of zeros, from 20% to 30%. If you take a large package of applications from Intel, there are 200 different applications that people use for computing - there are a lot of zeros. This is initialization, these are matrices with a large number of zeros, these are null pointers. There are many reasons for this.
Very often there are duplicate values. In some small area of memory, in the cache, very similar values can be repeated. This, for example, and if you work with graphics, you have a bunch of pixels, and if you have a part of a picture with the same colors, then you have all the pixels that are in a row going to be the same. In addition, narrow values, single-byte and two-byte values, which are stored in 2, 4 and 8 bytes. Why is this happening and whose error is this? Where does such redundancy come from?
Redundancy is related to how we program the code. We use some language, for example, C ++. If we want to allocate memory for some object, say, for a whole array, imagine that in the array we store statistics about some events, and these events can be both very frequent, say, billions, and single. For example, reference to memory with a specific instruction. Most instructions are not memorized, but some can be accessed billions of times during startup.
The programmer is forced to allocate an array of eight-byte numbers, because in the worst case, his integer values can take large values. However, this is redundant. Many of these values are not really needed, and there will be a bunch of incomplete zeros, but some of the leading zeros.
In addition, we have many other values that also have different types of redundancy. For example, pointers. Anyone who once debugged the code and looked at the pointers, you can see that they are changing quite large. But if you have pointers with approximately one memory area, then most of the bits ahead will be the same. This type of redundancy is also evident.
I have seen many types of redundancy. The first question is how many are there?

Here, the experiment in which I periodically took data from the second-level cache saved the snapshot of this cache and watched how many zeros there were, repeated values. On the X axis, various applications from the SPEC2006 package, which is actively used in the computer architecture, as well as other various applications from Intel, include both the database and various web workflows, such as the Apachi server, for example. And here is the assumption that this is a 2 megabyte L2 cache.
You may notice that there is a large variation between redundancy in different applications, but even these very simple patterns are quite common. Only they cover 43% of all cache lines, all data that is stored in the cache.
You can come up with something quite simple that will cover these and maybe some other patterns, and give us good compression performance.
However, the question is, what makes these patterns related? Will I have to do some kind of compression algorithm that will work specifically for each of these patterns, or can I do something in common?
The general was the idea of observation. All these values, they can be both large and small, there is very little difference between them. Roughly speaking, the dynamic range of values in each specific cache line is very small. And you can imagine the values stored in the cache, for example, the 32-byte cache line can be represented simply using Base + Delta Encoding.

Take, for example, the first value for the base, and all the others as an offset from this base. And since the values from each other differ in most cases not much, then our delta fits in one byte, and instead of 32 or 64 bytes we can do with only 12 bytes and save about 20 bytes of space.
I will not talk about all the details of how to implement it in real hardware. We made a real prototype, wrote a prototype on Verilog, drove it on modern FPGAs, talked to Intel about implementation. You can make an algorithm based on this idea, which will require only one or two clocks in decompression. This algorithm is applicable, and it gives a good compression ...

The best previous works that were used in the cache, gave about 50% of additional space. This is not a pure compression - it can give a lot more - this is a real bonus to effective compression, that is, how much cache looks to users. There are still any problems with fragmentation and so on that need to be addressed.
Compression is at the level of the best previous mechanisms that Intel had, but the main gain in the middle of the slide is decompression. The previous algorithms, they had the best decompression was 5-9 cycles. We managed to do it in 1-2 clocks, while the compression is also quite effective.
Algorithms of this kind can be done in real hardware and applied in the cache, for example, in memory.
The effect of applying such optimization in the cache leads to the fact that the cache looks to the user often almost twice as much in efficiency. What does it mean? If you look at the modern processor, in the photos, there are almost no cores themselves. There, most of the space is occupied by processor caches - 40-50% easily from both IBM and Intel. In fact, Intel can not just take and double the cache, there is simply no room for more cache. And such optimizations that cost only a few percent of the core itself are, of course, very interesting.
We worked with various optimizations in the second work, which I will not talk about today, about how to work with such caches, which now can have different cache line sizes. All these problems have been successfully resolved.
I want to talk about our third work, which was also done with Intel, about how to compress memory.
What problems are there?

The main problem is that if in Linux or Windows I have a 4 KB memory page, then in order to compress it, I need to solve the following problem: I need to solve the problem of how the data addresses on this page change. Initially, you have 4 KB, and each cache line in it is also 64 bytes. And the offset of any cache line inside this memory page is trivial to find: you take 64 and multiply by the offset you need.
However, if you use compression, each line is now potentially of a different size. And if you need to read some page from the memory now, you do not have these displacements.
We can say that you can save them somewhere. And where to keep them? Either again in memory or in cache. But if you want to save all offsets for each memory, you don’t have enough cache, you need resources of the order of hundreds of MB to serve all the memory. You cannot save this data in the chip, and you don’t want to store it in memory, because each memory access will now be several memory accesses. First you will go for the metadata, and then for the real data.

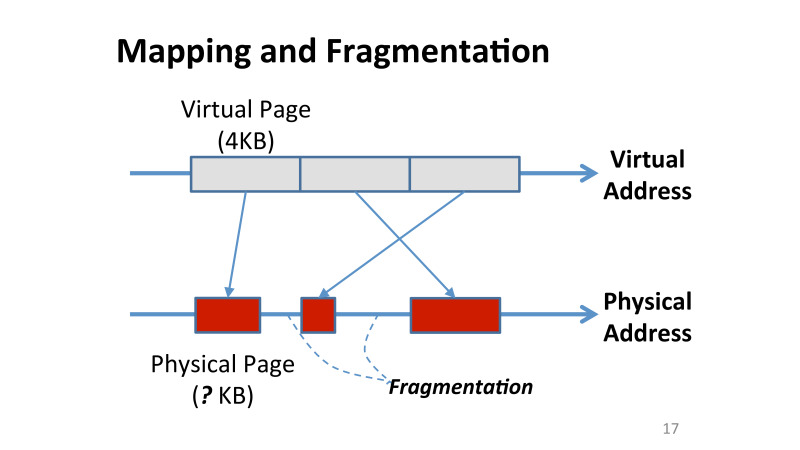
The second problem that everyone faced when working with the OS is data fragmentation. Here it becomes extremely complex, because each page also occupies a different place in memory. At the same time, in the virtual address space all pages are still 4 Kb, but after compression they all occupy completely different sizes. And this is a problem, how now to work with this empty place. The OS is not aware that we have allowed the pages to be made smaller, it just does not see these fragmented pieces. Just like that, without changing anything, we will not receive bonuses from compression.

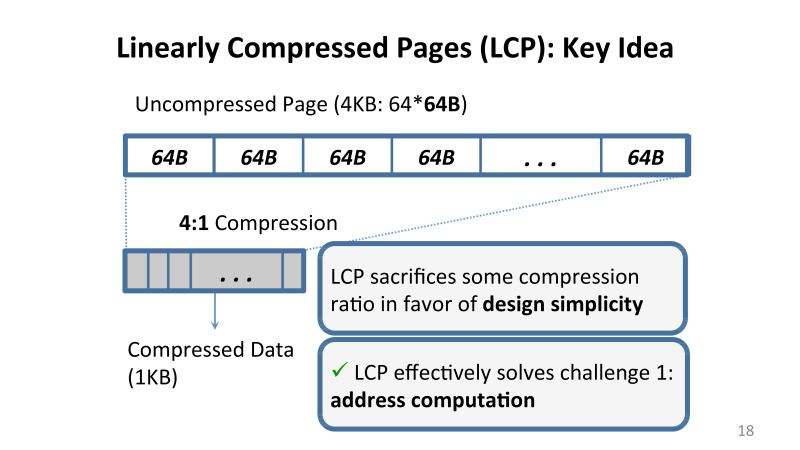
What did we suggest to solve this problem? Compression using a linear coefficient. We imposed a set of certain restrictions, which are described in detail in the article, but the bottom line is that if I apply compression to memory, I use an algorithm that ensures that every cache line on this page either compresses with a certain factor, say, 4 to 1, 3 to 1 or not compressed at all.
We potentially lose something in terms of data compression, because we impose additional restrictions, but the main bonus is that the design is very simple, it can be implemented, which we have successfully done, for example, in Linux.

Linearly Compressed Pages (LCP), a technique that we proposed, copes with the main problem that now the addresses of all the data are quite simple. We have a small block of metadata that is stored on the same page, and there are either original data that is stored in a compressed form, or the so-called exception storage, cache lines are stored there, which we could not compress in this way.
Based on these ideas, we managed to get good data compression, and most importantly, I compare it with the best previous works that were made mainly by IBM, they also had good algorithms for compression.

Our compression was not particularly better than theirs, but most importantly, we got more memory without paying extra performance for it. Roughly speaking, they got more memory, but for this they had a loss of performance, albeit small, but there was. . , , .
, . Nvidia. . , , 5-6 . bandwidth, .
, Nvidia, 2014 , , , . , : , DVFS, , , , , , , .
— , , . , , . . , - , , , . Nvidia , .

, , . . , , , 0011. . 0101. , 0 0, , bit toggle, , , , , , 0 1 1 0. , . , . , .
— , . , , networks of chip DRM , , .
What is going on? ?

Nvidia, . , 32 16 , . ? , . , , XOR, 16 8 , , .
- , , frequent pattern compression, Intel, , . 15, 16 . , , , alignment. , . , . , Nvidia . , , , , . , 2%, 40%. , .
, . , , , , , , , , , , .

. , , , . , , , - , — , . , , . , , , , , .
, , , Microsoft Research , machine learning.
, , , , . DNNs. . , DNNs — , - Ajura, , , , . , 10%. , , , : TensorFlow, CNTK, MXNet. , , .
DNNs , , , GPU.

DNNs . , , , , . . , , , , . , .
, . , , inference.

, Google TPU , , , inferent , , Microsoft.
? ? Google, , TPU inference. , . , inference, . forward pass. , - , inference . — . , . backward pass, , , .
, , . , . , , feature maps activations. inference , . back propagation, , , , . , L2, , forward pass , , , , .
, , 100, 200 , , ResNet, image classification. - . — , , ResNet 101 , , , - mini batch , , 64 , , , 16 . , P100 Pascal Volt100, 16 . , .
, Facebook, . , , , . , .
, . GPU, . , .

, , , , , . X AlexNet, DNN , : Overfeat, VGG16, Inception ( Google version 3, , Google). mini batch. , , . , , ImageNet, 220 220 3, 1000 : , , .
? AlexNet , 2011 , . , , feature maps, .
? , , mini batch, , , inputs. ? GPU . GPU 8000 threads, , , GPU . , ? , CPU ISAC.
, . , . , , , , , , , DNN inference, , ISCA, MICRO, 2015 15 , deep neural networks, inference, .
-, inference, , forward pass, , , .
, , . , inference, - , , 32- floating point, , 16 , 8 4. , , - stochastic gradient descend, . , . GPU, ISAC, - TPU - FPGA . GPU .

, . , , , , , , , , , , , LX, . , , . . : .
, . - , . , . . . , . , . , . .
, , ? , . , , . , , , . , . - , .

, , : feature maps . , , , , . , , , Relu , rectified linear function pulling layer, , , .
, , . , . , , , Relu, pulling layer. layers, .
, Relu , , - — . — .

, Relu, . , . Relu — , , , 0, . — , , .
, , , by modal. . , , . , , . - , 32 , , , 31 . , , .
32 , . . , . , pulling layer — 2 2, , 2 2 3 3. , , , . TensorFlow, CNTK, , , . , , machine learning, , . . , , , - , , .
- , , , , . Relu 32 , pulling layer 8 . , , TensorFlow, . - . .
, 32 1 . , , . , . 32-, , . .
, lossless, .

, Relu . . , , VGG16, 10 , , — , . 1 100% , 0,6 — 60% . , .
, , Relu_1, Relu_2 , . , , 60%, 70%. , , , . , .
What does it mean? , . , , GPU. CUDA , . , - CUDA . , NVidia , 99%. . , 50% 80% . , GPU . , , , CUDNN , Nvidia . , CUDA , .
, , , Lossy Encoding, . , IBM . , L1 - . 32 , 8 16, - , .
, 32- 16- , , , , , , AlexNet, 32 16 - , , , , validation. , , . , , , . , , , .
. , , , . , , . — . forward pass . , , backward pass, . backward pass, .
?

, . — AlexNet FP32, 32 . , IBM , All-FP16, 16 , . - 16 , , 16 , , , - .
, , , , 16 , 8 . , .
, , . , , .

, Gist, «». DNN, execution graph, , , , CNTK , Microsoft. CUDA . execution graph, , TensorFlow, MXNet, . GPU , , . , , .
, , , cuDNN, , . . . , TensorFlow. GIST .

, , ? . , , , , , , 90-100 , . . , , . 6% 8%, , , , . , , Microsoft.
, . , , Microsoft, PhD , , DNN Training, , , , , . . Microsoft , LSTM , speech , , . - -, .
. , , . image classification, AlexNet, ResNet , . Image classification — , , , Facebook. , machine learning .
, , , . , . , MXNet, Amazon, , , TensorFlow. ResNet 50, , «» , 40% , TensorFlow . , MXNet , TensorFlow? . . LSTM, MXNet , TensorFlow, - , Amazon Google, TensorFlow 2,5 . , . .
, . , . , , , , machine learning, .
, , Image Classification, , . object detection, , , Faster RCNNs, 16-17- Google MIT, . : LSTM, , , . nmt — Google, open source. sockeye Amazon. .
Transformer, Attention layers. 2013-, , , , , Attention layers. Google , GPU, , .
speech recognition, LSTM. adversarial networks, reinforcement learning, Google AlphaGo . supervise, n-supervise learning. image classification. , . 16-17- , .
, . TensorFlow, CNTK, MXNet. , , , . TensorFlow , - CNTK MXNet. , , , . , , .
. GPU. , CPU . , , GPU, FPGA, ISAC Google. , TensorFlow, .
: , , , , -. .
, , , , . , , , CNTK. . , . TensorFlow , , 2000 , , , , . . , CNTK, MXNet. TensorFlow , . , Google … , , , , , .
, .

, TensorFlow MXNet . , NMT Google, Sockeye. , - , LSTM , batch, , .
, , , -, Y blue score. , , . , . .
? , , , blue score 20 . , , . SGD. , , - , .
- , learning rate , -, . . , , , , , , . , TensorFlow LSTM . CUDNN, MXNet LSTM. , .
, , TensorFlow, MXNet. , GPU, LSTM , 30% GPU . 70% . , , . TensorFlow 10-15%, . , MXNet. .
LSTM, , Nvidia CUDNN , LSTM . , . -, E , , CUDNN 2,5 LSTM. , «» P100 CUDNN 8 , «» 100 CUDNN 9 . . , . .

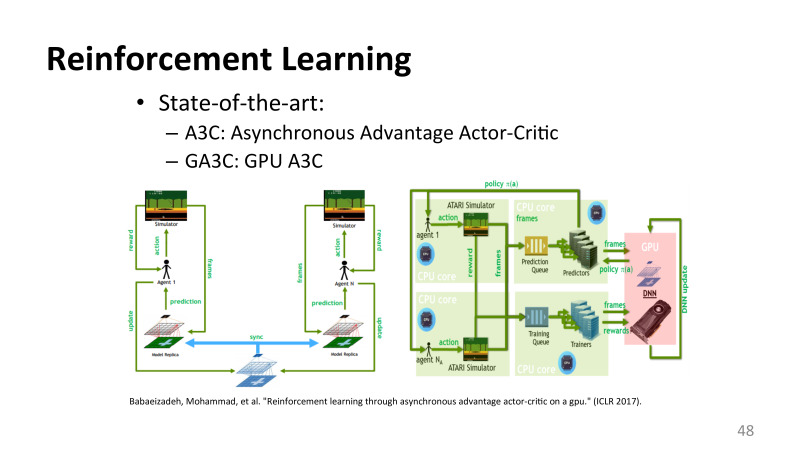
reinforcement learning, . , NIPS ICLR, . , machine learning MATLAB . , , . , , , . . Google, , .
, - , . .

reinforcement learning, MXNet TensorFlow, , .
, . , , , , , , . , , .
, , : , . What does it mean? , , . , - , , . , . , Google , 5-7%.

cloud tax 20–25%, , , . , Google Cloud, 25% — , .
— . , - , ? , , , .

, . . , -, - . - , - . . , , , . , where value = 10, value . , .
, 4 .

, , , Base+Delta Encoding, - . , 1 , . .
, -. , , ? - , , . , , - , n . , , , . , Base+Delta Encoding . , , Base+Delta Encoding.
What does it mean? , , . .
, , , , , , .
, 1 — , . , , — . , . . , CND- Intel . , 1 , . 4 8 .
, . . , , . , . It's all.
Source: https://habr.com/ru/post/350896/
All Articles