Solve problems without self-balancing trees in Python
Many algorithmic tasks require knowledge of certain data structures. The stack, the queue, the heap, the dynamic array, the binary search tree — the solution of an algorithmic problem rarely does without using any of them. However, their high-quality implementation is not a trivial task, and when writing code you always want to do the maximum using the standard language library.
As for Python, it has almost everything.
But there is no self-balancing search tree, as such, in the standard library. It's a pity!
')
In this article I will examine several algorithmic problems that involve solving using a binary tree, and show you how to replace it in different situations in Python.
You probably already know that the self-balancing binary search tree is the most convenient data structure for many tasks, supporting many operations. But just in case I will list them and recall their asymptotic complexity.
And much more (probably). In general, having a tree at hand is very, very convenient. Well, move on to the tasks!
On a straight line are skyscrapers, some of which overlap each other. It is necessary to describe the outlines against the sky of the entire set of skyscrapers.

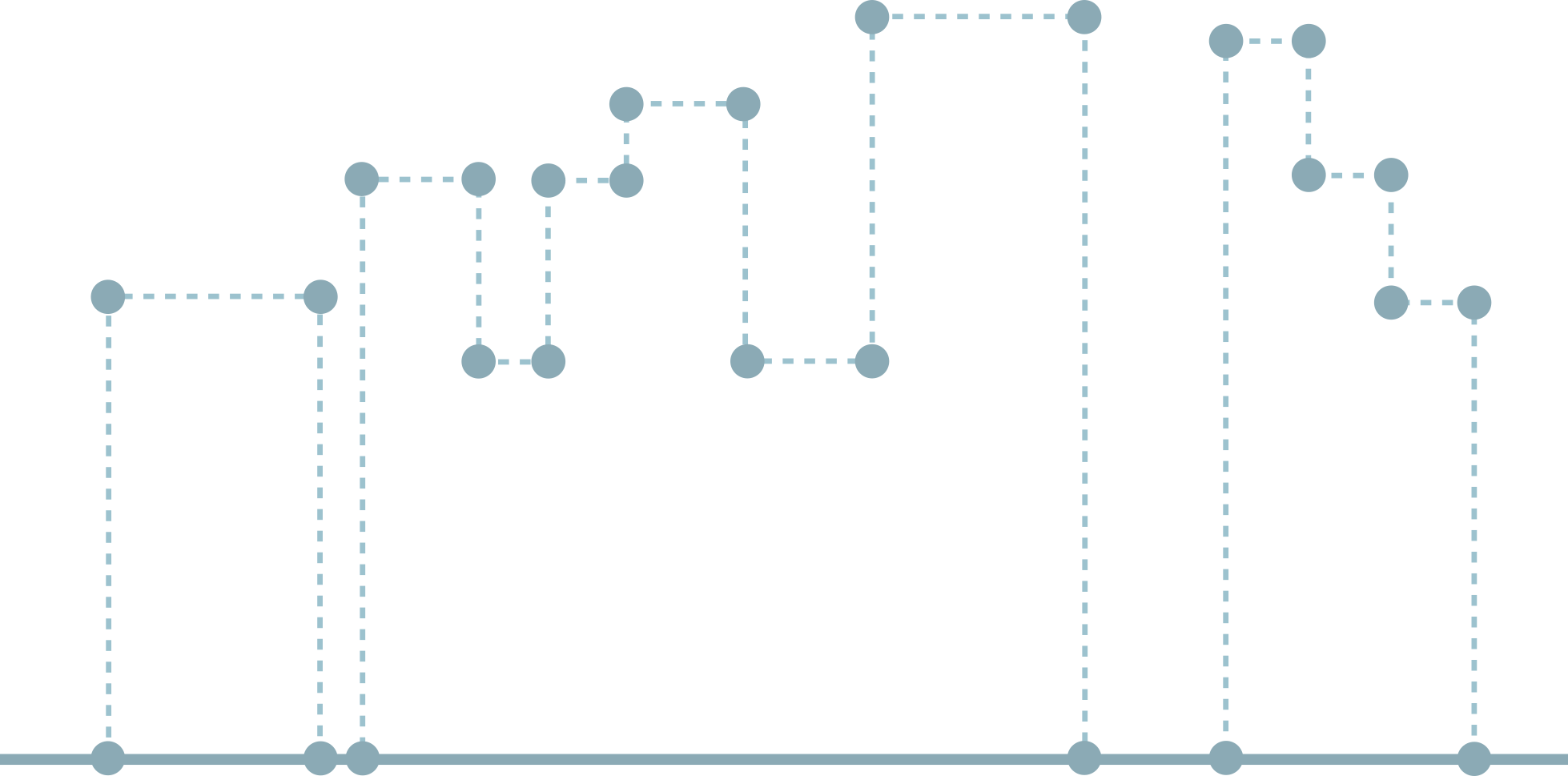
Buildings are described as an array of view tuples (coordinate of the left edge of the building, coordinate of the right edge of the building, height). At the exit you need to pass an array of tuples (x, y), describing the general silhouette of buildings.
This problem is solved for . The algorithm as a whole is approximately the following: we sort all points (both left and right edges of buildings), we go along them from left to right. If you stumbled upon the left edge of the building - you need to add it to the list of currently active, if the right - to exclude from the list. In any case, each time it is necessary to check whether the maximum height of the active buildings has changed, and if it has changed, record the next point in response. (A more detailed analysis of this problem can be found here .)
The list of active buildings, as a data structure, must support the rapid addition of a new element, the removal of an arbitrary element and the finding of a maximum. Binary tree can do all three operations for and perfect for this task. Let's try to do without it!
The need to quickly take the maximum, of course, reminds us of the heap. But the heap does not provide for the removal of an arbitrary element! For example, to remove a heap item with a known index in Python within a reasonable time, you need to get into the non-standardized implementation details of the
( This code is taken from the response to StackOverflow .)
However, it is possible to make an add-on over the heap, which allows you to delete an arbitrary element for the cushioned . The algorithm is as follows:
It remains only to note that the elements can be repeated.
Code:
This task is found in different variants. Most generally, taking into account the specifics of Python, it can be formulated as follows: the algorithm is fed as an input by an iterator of unknown (and, possibly, unlimited) length. It is necessary to return an iterator with medians for all windows of a predetermined width. .
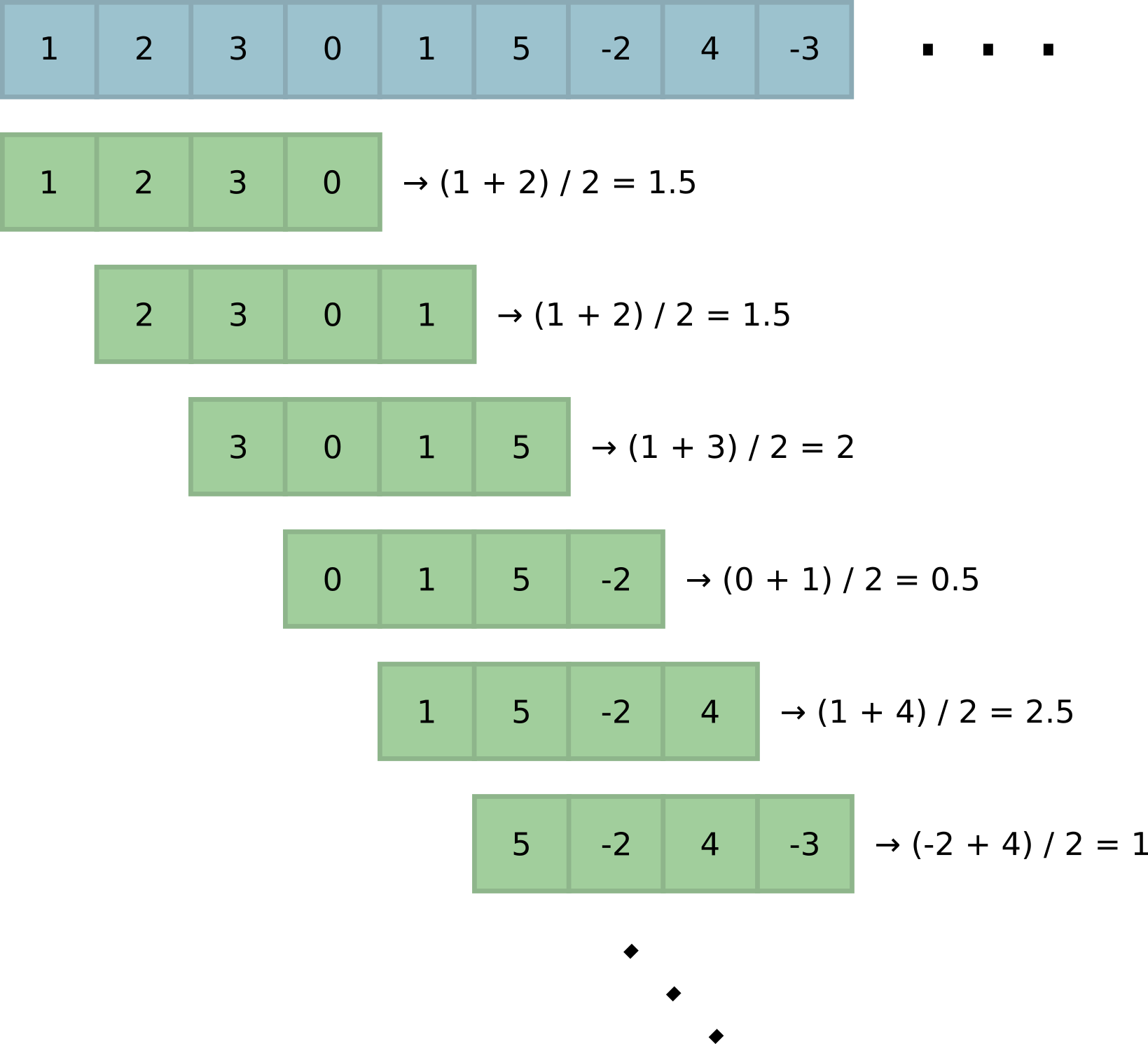
With the optimal solution of this problem, each next median is calculated for the amortized . Like most tasks on a sliding window, the solution is to build a data structure that allows you to quickly add a new element to the window, delete the oldest element and calculate the next median.
The tree obviously solves this problem. Adding, removing and finding the median for give optimal asymptotics for our version of the problem. There is also a way to reduce the difficulty of finding the median to a depreciated : to do this, remember the pointer to the median element (or two elements, the arithmetic mean of which gives the median if even) and update it when adding and deleting elements (the update will cost a depreciated - think why!).
If you think the elements needed to find the median, in the tree can only be in three places:
The words "smallest" and "greatest", of course, again remind us of the heaps!
Indeed, let's store two heaps, a min-heap and a max-heap, in a balanced size. At the same time, all max-heap elements should be smaller than all min-heap elements. When adding an element, you need to put it in the correct heap and balance them: this will require a finite number of operations like “extract the extreme value from one heap and put it into another” . Getting the median is worth , because for this you need only a maximum of max-heaps and a minimum of min-heaps.
Code:
(For this code, I added
The solution of the problem with this data structure becomes elementary:
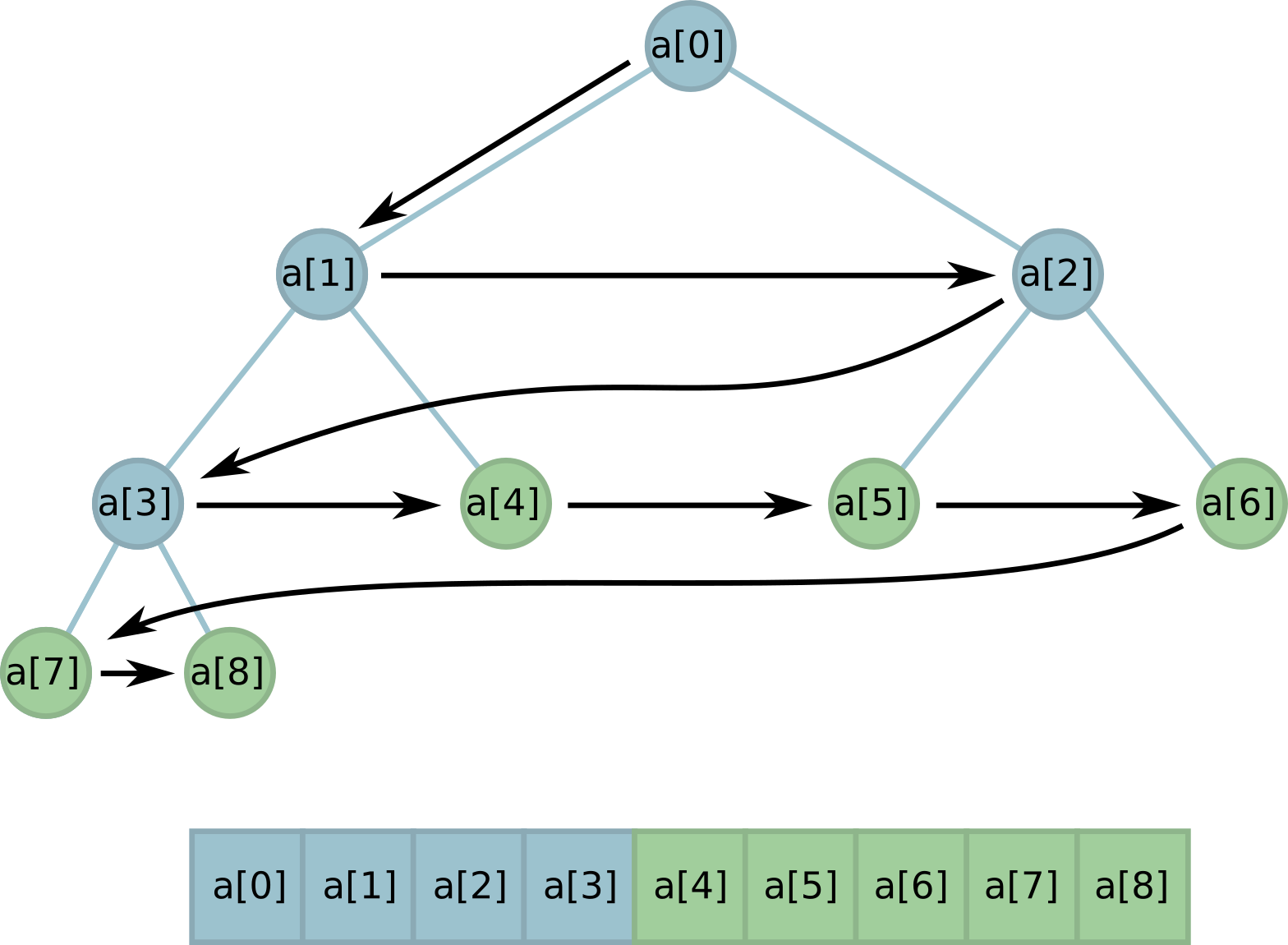
Dan array of numbers It is necessary to calculate the number of pairs of array elements that are in the wrong order, that is, when takes place If an array consists of different numbers from 1 to n, then the parity of this number is nothing but the parity of the permutation described by this array.
The task is also generalized to the case when the bad pairs are those for which and where - some positive coefficient.
In both cases, it is decided for memory and time (except in the case of a permutation in which it is solved for - but that's another story. An elementary solution with a tree looks like this: go through the array, at each step add to the answer the number of elements greater than the current one (or the current one, multiplied by ) - the tree does it for - and after that we add the current element to the tree.
There are already some heaps can not do!
But without a tree can not do too. Implementing a tree is easy; but if it is not balanced, then in the worst case asymptotics worsen to ! What to do?
Let's expand the task and go from the other end. After all, you can first build the entire tree, at each step of the cycle, delete the current element from it and add to the answer the number of elements less than the current one. It is easy to build a balanced tree - it is enough to initially sort the array and write a competent recursion:
But the removal from the tree - a dreary exercise. An unsuccessful deletion algorithm can ruin a tree and again make it an unacceptable height! Therefore, let's not remove nodes from the tree, but only mark them as deleted. Then with the height of the tree for the entire time of the algorithm, nothing is guaranteed to happen and we get the coveted .
However, with this approach, the presence of nodes with repetitive elements (especially in large quantities) can seriously ruin life. Therefore, before building a tree, it makes sense to deduplicate the elements with a multiplicity calculation.
Code:
The solution of the problem is accordingly elementary again:
This task does not require self-balancing trees at all - I bring it as a bonus to tell you a little more about the trees in Python.
There is a virtual basket with balls of different colors. In the basket you can put a ball of a certain color, and you can pull out a random ball. The task is to program this basket programmatically with the most efficient operations.
The obvious solution is operations to add a ball and the choice of random: store an array with the number of balls of each color and the total number of balls N, if necessary, select a random ball, generate a random number from 0 to N - 1 and see where it falls. (For example, there are 2 balls of zero color, 1 ball of the first color and 4 balls of the second. If a drop of 0 or 1, a ball of zero color came out; if 2, then the first color; if 3, 4, 5 or 6 - the second color.)
However, you can arrange the basket so that both operations cost . To do this, the number of balls of each color must be stored in the leaves of the tree, and in the remaining nodes - the amount of all the leaves in the corresponding subtrees.
Since k is given, we know in advance how many leaves will be in the tree. The number of nodes also can not change. Total we have a tree of constant size; when we try to calculate this size, we notice that it has another special property.
Suppose we know how many nodes we need. Let's try to put the whole tree in an array, as Python does in the
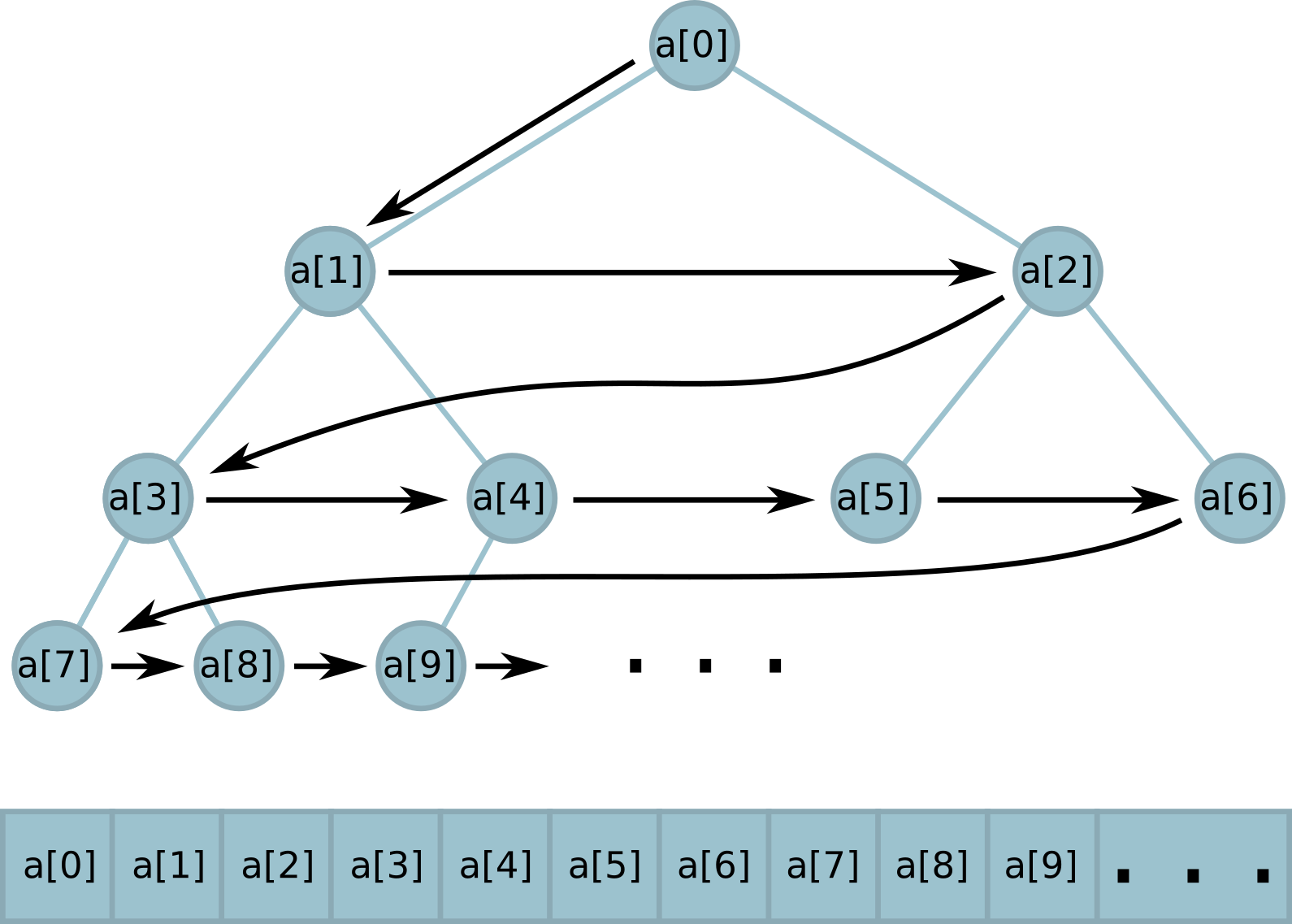
Each node has its own index in the array. At the root, this index is 0, in children of the node with index
We need a certain number of leaves in the tree. It is easy when this number is a power of two. The leaves in this case simply occupy a whole layer of the tree and in memory are arranged in a row.
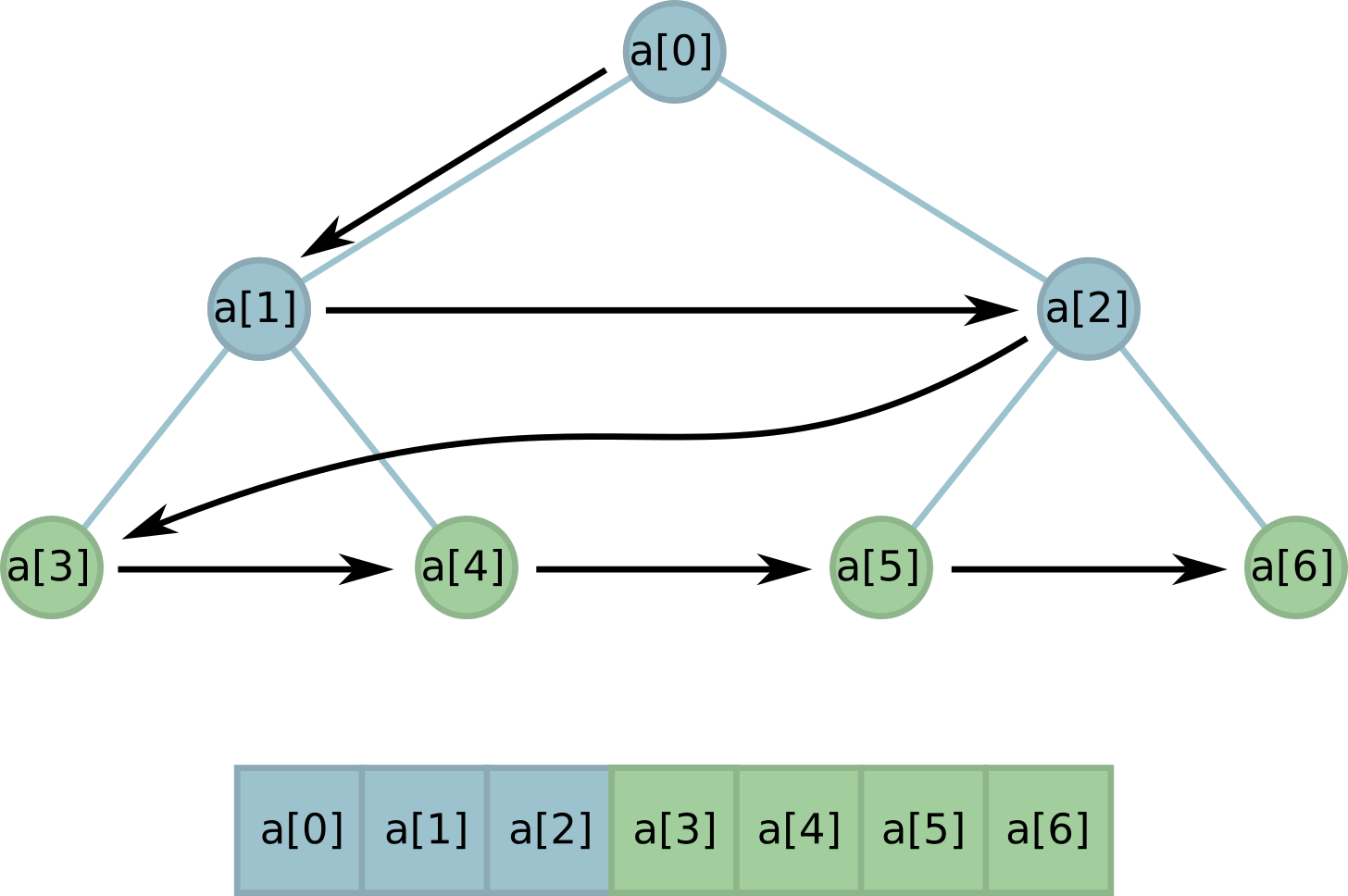
But what if k is between two powers of two? Well, we can open several buds (necessarily from the left edge!), So that the number of leaves is as we need:
Note that while all the leaves are still located in memory in a row ! This useful feature will help us greatly in implementation.
It remains only to calculate how many nodes are needed for a tree with a given number of leaves k. When k is a power of two, everything is clear: everything in the tree will be knots. Surprisingly, in all other cases too!
Code:
Yes, most of these tasks have solutions without any trees at all. Nevertheless, I believe that trying to solve them was a useful exercise. I hope for you too! Thanks for attention.
As for Python, it has almost everything.
- Dynamic array - built-in type
list. It also supports stack operations:.append()and.pop(). - The hash table is the built-in types
setanddict, and also the immutable brother of the setfrozenset. - Heap -
listwith special insert and delete operations implemented in theheapqmodule. - A two-way queue is the type
dequedescribed in thecollectionsmodule.
But there is no self-balancing search tree, as such, in the standard library. It's a pity!
')
In this article I will examine several algorithmic problems that involve solving using a binary tree, and show you how to replace it in different situations in Python.
What the search tree is capable of
You probably already know that the self-balancing binary search tree is the most convenient data structure for many tasks, supporting many operations. But just in case I will list them and recall their asymptotic complexity.
- Insert item - worth
- Deleting an item is worth
- Item Search - Worth
- Finding the minimum and maximum elements - worth . If necessary, you can remember the pointers to them; then the need for tree passage is eliminated and the cost is reduced to
- Finding the median, and indeed any k-th ordinal statistics - is In this case, it is necessary to remember in each node of the tree the size of the corresponding subtree.
- Finding the number of elements less / more than the specified value For this, it is also necessary to remember the size of the corresponding subtree in each node of the tree.
- Inserting a monotonous sequence of elements - may cost depreciated for everyone! (Did you know that in C ++,
std::setcan be filled from a sorted array in ?)
And much more (probably). In general, having a tree at hand is very, very convenient. Well, move on to the tasks!
Task: skyscrapers
On a straight line are skyscrapers, some of which overlap each other. It is necessary to describe the outlines against the sky of the entire set of skyscrapers.


Buildings are described as an array of view tuples (coordinate of the left edge of the building, coordinate of the right edge of the building, height). At the exit you need to pass an array of tuples (x, y), describing the general silhouette of buildings.
This problem is solved for . The algorithm as a whole is approximately the following: we sort all points (both left and right edges of buildings), we go along them from left to right. If you stumbled upon the left edge of the building - you need to add it to the list of currently active, if the right - to exclude from the list. In any case, each time it is necessary to check whether the maximum height of the active buildings has changed, and if it has changed, record the next point in response. (A more detailed analysis of this problem can be found here .)
The list of active buildings, as a data structure, must support the rapid addition of a new element, the removal of an arbitrary element and the finding of a maximum. Binary tree can do all three operations for and perfect for this task. Let's try to do without it!
The need to quickly take the maximum, of course, reminds us of the heap. But the heap does not provide for the removal of an arbitrary element! For example, to remove a heap item with a known index in Python within a reasonable time, you need to get into the non-standardized implementation details of the
heapq module (which is, of course, unreliable and not recommended): def heapremove(h, i): h[i] = h[-1] h.pop() if i < len(h): heapq._siftup(h, i) heapq._siftdown(h, 0, i) ( This code is taken from the response to StackOverflow .)
However, it is possible to make an add-on over the heap, which allows you to delete an arbitrary element for the cushioned . The algorithm is as follows:
- We store along with a bunch of many deleted items.
- If you want to delete an element that is not currently the minimum on the heap, add it to the set of deleted elements.
- If you want to delete an element that is now minimal, delete it with the standard
heappop. If the new minimal element is contained in the set of deleted elements, delete it, and so on.
It remains only to note that the elements can be repeated.
Code:
class HeapWithRemoval(object): def __init__(self): self.heap = [] # set, self.deleted = collections.defaultdict(int) def add(self, value): if self.deleted[value]: self.deleted[value] -= 1 else: heapq.heappush(self.heap, value) def remove(self, value): self.deleted[value] += 1 while self.heap and self.deleted[self.heap[0]]: self.deleted[self.heap[0]] -= 1 heapq.heappop(self.heap) def minimum(self): return self.heap[0] if self.heap else None Task: median in a sliding window
This task is found in different variants. Most generally, taking into account the specifics of Python, it can be formulated as follows: the algorithm is fed as an input by an iterator of unknown (and, possibly, unlimited) length. It is necessary to return an iterator with medians for all windows of a predetermined width. .

With the optimal solution of this problem, each next median is calculated for the amortized . Like most tasks on a sliding window, the solution is to build a data structure that allows you to quickly add a new element to the window, delete the oldest element and calculate the next median.
The tree obviously solves this problem. Adding, removing and finding the median for give optimal asymptotics for our version of the problem. There is also a way to reduce the difficulty of finding the median to a depreciated : to do this, remember the pointer to the median element (or two elements, the arithmetic mean of which gives the median if even) and update it when adding and deleting elements (the update will cost a depreciated - think why!).
If you think the elements needed to find the median, in the tree can only be in three places:
- fundamentally;
- in the smallest element of the right subtree;
- in the largest element of the left subtree.
The words "smallest" and "greatest", of course, again remind us of the heaps!
Indeed, let's store two heaps, a min-heap and a max-heap, in a balanced size. At the same time, all max-heap elements should be smaller than all min-heap elements. When adding an element, you need to put it in the correct heap and balance them: this will require a finite number of operations like “extract the extreme value from one heap and put it into another” . Getting the median is worth , because for this you need only a maximum of max-heaps and a minimum of min-heaps.
Code:
class MedianFinder(object): def __init__(self, k): self.k = k self.smaller_heap = HeapWithRemoval() self.larger_heap = HeapWithRemoval() # , : self.elements = deque([], k) def add(self, num): if len(self.elements) == self.k: # - . . element_to_delete = self.elements[0] if self.smaller_heap and element_to_delete <= -self.smaller_heap.minimum(): self.smaller_heap.remove(-element_to_delete) else: self.larger_heap.remove(element_to_delete) self.balance() # . if self.larger_heap and num >= self.larger_heap.minimum(): self.larger_heap.add(num) else: self.smaller_heap.add(-num) self.elements.append(num) self.balance() def balance(self): # , . if len(self.larger_heap) > len(self.smaller_heap) + 1: num = self.larger_heap.pop() self.smaller_heap.add(-num) elif len(self.smaller_heap) > len(self.larger_heap) + 1: num = -self.smaller_heap.pop() self.larger_heap.add(num) def median(self): if len(self.larger_heap) > len(self.smaller_heap): return self.larger_heap.minimum() if len(self.larger_heap) < len(self.smaller_heap): return -self.smaller_heap.minimum() return (self.larger_heap.minimum() - self.smaller_heap.minimum()) / 2 (For this code, I added
pop methods to HeapWithRemoval ,__len__ and __nonzero__ .)The solution of the problem with this data structure becomes elementary:
def median_over_sliding_window(input, k): finder = MedianFinder(k) for num in input: finder.add(num) if len(finder.elements) == k: yield finder.median() Task: number of inversions
Dan array of numbers It is necessary to calculate the number of pairs of array elements that are in the wrong order, that is, when takes place If an array consists of different numbers from 1 to n, then the parity of this number is nothing but the parity of the permutation described by this array.
The task is also generalized to the case when the bad pairs are those for which and where - some positive coefficient.
In both cases, it is decided for memory and time (except in the case of a permutation in which it is solved for - but that's another story. An elementary solution with a tree looks like this: go through the array, at each step add to the answer the number of elements greater than the current one (or the current one, multiplied by ) - the tree does it for - and after that we add the current element to the tree.
There are already some heaps can not do!
But without a tree can not do too. Implementing a tree is easy; but if it is not balanced, then in the worst case asymptotics worsen to ! What to do?
Let's expand the task and go from the other end. After all, you can first build the entire tree, at each step of the cycle, delete the current element from it and add to the answer the number of elements less than the current one. It is easy to build a balanced tree - it is enough to initially sort the array and write a competent recursion:
import collections Node = collections.namedtuple("Node", "value left right") def make_tree(nums): nums = sorted(nums) return _make_tree(nums, 0, len(nums)) def _make_tree(nums, l, r): # . # [l, r). if r - l <= 0: return None if r - l == 1: return Node(nums[l], None, None) center = (l + r) // 2 left_subtree = _make_tree(nums, l, center) right_subtree = _make_tree(nums, center + 1, r) return Node(nums[center], left_subtree, right_subtree) But the removal from the tree - a dreary exercise. An unsuccessful deletion algorithm can ruin a tree and again make it an unacceptable height! Therefore, let's not remove nodes from the tree, but only mark them as deleted. Then with the height of the tree for the entire time of the algorithm, nothing is guaranteed to happen and we get the coveted .
However, with this approach, the presence of nodes with repetitive elements (especially in large quantities) can seriously ruin life. Therefore, before building a tree, it makes sense to deduplicate the elements with a multiplicity calculation.
Code:
import collections class Node(object): def __init__(self, value, smaller, larger, total_count): self.smaller = smaller # self.larger = larger # self.value = value self.total_count = total_count # def count_smaller(self, value): if not self.total_count: # ? return 0 if value <= self.value: return self.smaller.count_smaller(value) if self.smaller else 0 if self.larger: larger = self.larger.total_count - self.larger.count_smaller(value) return self.total_count - larger return self.total_count def remove(self, value): # . . while True: self.total_count -= 1 if value == self.value: return self = self.smaller if value < self.value else self.larger def make_tree(nums): nums = sorted(nums) counter = collections.Counter(nums) return _make_tree(nums, counter, 0, len(nums)) def _make_tree(nums, counter, l, r): # # . [l, r). if r - l <= 0: return None if r - l == 1: return Node(nums[l], None, None, counter[nums[l]]) center = (l + r) // 2 left_subtree = _make_tree(nums, counter, l, center) right_subtree = _make_tree(nums, counter, center + 1, r) value = nums[center] # , . total_count = counter[value] + \ (left_subtree.total_count if left_subtree else 0) + \ (right_subtree.total_count if right_subtree else 0) return Node(value, left_subtree, right_subtree, total_count) The solution of the problem is accordingly elementary again:
def count_inversions(nums, coef=1.0): tree = make_tree(nums) result = 0 for num in nums: tree.remove(num) result += tree.count_smaller(num * coef) return result Bonus task: basket with balls
This task does not require self-balancing trees at all - I bring it as a bonus to tell you a little more about the trees in Python.
There is a virtual basket with balls of different colors. In the basket you can put a ball of a certain color, and you can pull out a random ball. The task is to program this basket programmatically with the most efficient operations.
The obvious solution is operations to add a ball and the choice of random: store an array with the number of balls of each color and the total number of balls N, if necessary, select a random ball, generate a random number from 0 to N - 1 and see where it falls. (For example, there are 2 balls of zero color, 1 ball of the first color and 4 balls of the second. If a drop of 0 or 1, a ball of zero color came out; if 2, then the first color; if 3, 4, 5 or 6 - the second color.)
However, you can arrange the basket so that both operations cost . To do this, the number of balls of each color must be stored in the leaves of the tree, and in the remaining nodes - the amount of all the leaves in the corresponding subtrees.
Since k is given, we know in advance how many leaves will be in the tree. The number of nodes also can not change. Total we have a tree of constant size; when we try to calculate this size, we notice that it has another special property.
Suppose we know how many nodes we need. Let's try to put the whole tree in an array, as Python does in the
heapq module:
Each node has its own index in the array. At the root, this index is 0, in children of the node with index
i , the indices are (2 * i + 1) for the left and (2 * i + 2) for the right; at the parent of the node with the index i index (i - 1) // 2 .We need a certain number of leaves in the tree. It is easy when this number is a power of two. The leaves in this case simply occupy a whole layer of the tree and in memory are arranged in a row.

But what if k is between two powers of two? Well, we can open several buds (necessarily from the left edge!), So that the number of leaves is as we need:

Note that while all the leaves are still located in memory in a row ! This useful feature will help us greatly in implementation.
It remains only to calculate how many nodes are needed for a tree with a given number of leaves k. When k is a power of two, everything is clear: everything in the tree will be knots. Surprisingly, in all other cases too!
Evidence
We are looking for a tree of minimal height with k leaves and skewed toward the left subtree if it is needed (that is, if k is not a power of two).
If a such a tree consists of one (leaf) node and for it the formula is correct.
If a and a power of two, the formula is again correct.
If a and not a power of two, you need to build a tree with two subtrees that satisfy the desired property (and guaranteed non-empty!). For them, the formula will be true; in the first will leaves, in the second - leaves ( ), and we have a total number of nodes
If a such a tree consists of one (leaf) node and for it the formula is correct.
If a and a power of two, the formula is again correct.
If a and not a power of two, you need to build a tree with two subtrees that satisfy the desired property (and guaranteed non-empty!). For them, the formula will be true; in the first will leaves, in the second - leaves ( ), and we have a total number of nodes
Code:
import random class Bucket(object): def __init__(self, k): self.k = k # , # . self.tree = [0] * (2 * k - 1) def add_ball(self, color): # ! node_index = self.k - 1 + color while node_index >= 0: # # . self.tree[node_index] += 1 node_index = (node_index - 1) // 2 def pick_ball(self): total_balls = self.tree[0] ball_index = random.randrange(total_balls) node_index = 0 # , , - # (k - 1). while node_index < self.k - 1: self.tree[node_index] -= 1 left_child_index = 2 * node_index + 1 right_child_index = 2 * node_index + 2 if ball_index < self.tree[left_child_index]: node_index = left_child_index else: ball_index -= self.tree[left_child_index] node_index = right_child_index self.tree[node_index] -= 1 return node_index - self.k + 1 PS
Yes, most of these tasks have solutions without any trees at all. Nevertheless, I believe that trying to solve them was a useful exercise. I hope for you too! Thanks for attention.
Source: https://habr.com/ru/post/350732/
All Articles