Bathroom mosaic and Diophantine equations

It was evening before bedtime. I brushed my teeth and wearily looked at the mosaic in the bathroom. For some reason, I was interested in such a simple fact: if a rectangle of 2 × 3 cells is rounded on both sides with cells, then the stroke area will be the same as the area of ​​the rectangle:

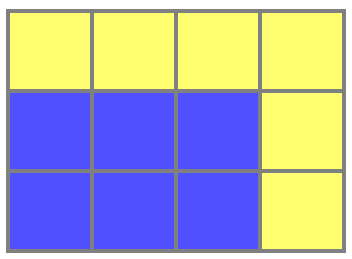
There are exactly as many blue squares as yellow ones. And then I suffered.

I wondered if there are more similar configurations. That is, to a rectangle $$$a \ times b$ draw a contour from two sides, and the contour area coincided with the area of ​​the rectangle. Of course $$$a$ and $$$b$ must be whole:

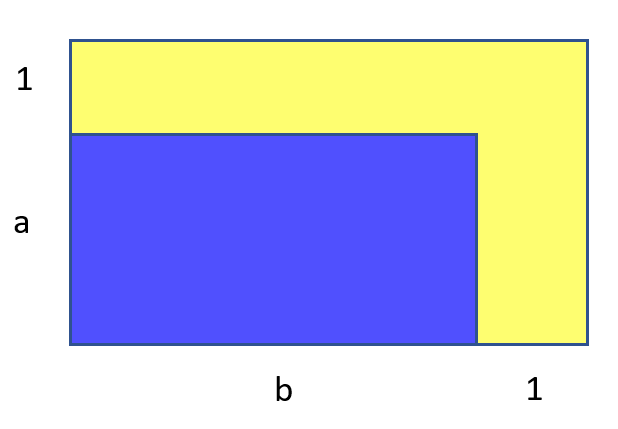
It seems that such cases should no longer be. Blue area $$$a \ times b$ , and yellow - $$$a + b + 1$ . It is seen that if $$$a$ or $$$b$ one, then there will be no coincidence, and if you increase them more $$$2 \ times 3$ , the blue will obviously grow faster. So this configuration is one.

Bored, said the brain. We must weaken the task. So to speak:

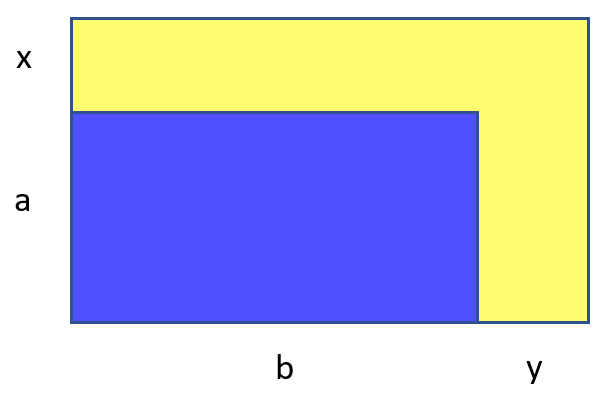
But now the task is too weak. In fact, it is necessary to choose two rectangles with integer sides, so that their areas differ exactly by half. And the only restriction on the rectangles is that one can be shoved into the other. There are too many, too boring. Let's go like this:

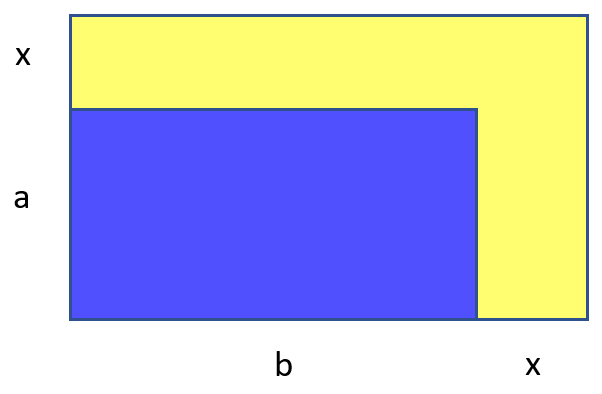
Fix the width of the edging. Are there many such? Hm Looks more interesting. Yellow Square is $$$(x + a) (x + b) - ab$ and we want it to be just $$$ab$ . That is, we (me and my brain, which has pulled me into this) need to solve the equation:

$$

$$(x + a) (x + b) - ab = ab$$

Or, which is the same:

$$

$$x ^ 2 + ax + bx - ab = 0$$

By this time I was done with my teeth and began to pour the powder into the dishwasher. Aha, said the brain, a good challenge. It is necessary to solve, of course, in integers, that is, this is a Diophantine equation . We did not pass the Diophantine equations at the university, but I remembered something about popular articles about them. Namely:

• If we have a homogeneous equation, then we are lucky.
• A homogeneous equation on integers can be easily turned into an equation on rational ones, reducing the number of variables by one.
• If by a method of close peering to find any root of a quadratic equation on rational numbers, then it is easy to find all the others.
• Any line with rational coefficients passing through a known root will pass through another root. Twisting this line, you can get all the rational roots.

In this way, for example, the general formula for all Pythagorean triples is easily found. By the way, as with the Pythagorean triples, in our problem any number of multiple solutions. For example, a rectangle $$$4 \ times 6$ You can expand the edging in two squares and so on. Of course, we are interested only in non-multiple decisions.

Will I be able to do all this in my mind, I thought, picking up a humidifier. Algebra without a piece of paper and a computer is a rather insidious thing: mixed up with a minus or forgot some member, and further calculations for nothing. Programmers know what to do to reduce the likelihood of an error - it is necessary to overlap with unit tests. Fortunately, we already know one solution: $$$x = 1; a = 2; b = 3$ . We will check it at every step.

$$

$$1 ^ 2 + 2 \ times 1 + 3 \ times 1 - 2 \ times 3 = 0$$

So far, so good. So, we have a homogeneous equation - all terms are in the second degree. Let's divide the equation by $$$x ^ 2$ (happening $$$x = 0$ we are not interested, so it is possible to divide):

$$

$$1 + \ frac a x + \ frac b x - \ frac a x \ times \ frac b x = 0$$

We make a replacement: $$$p = a / x; q = b / x$ and we get an equation with two rational variables:

$$

$$1 + p + q - pq = 0$$

In our unit test $$$p = 2; q = 3$ , the test passes. Now we must draw a straight line. In principle, it can be carried out just through the point $$$(2; 3)$ but it's hard to keep in the brain. But by the method of intent peering, we can easily find another point that satisfies the equation: $$$p = -1; q = 0$ . This corresponds to zero area. $$$a \ times b$ and again as a solution is not very interesting, but for holding a straight just right. It’s pretty easy to see that all the lines (except one) going through $$$p = -1; q = 0$ described by an explicit equation $$$q = \ alpha (p + 1)$ (yes, for some reason, the brain issued a Greek letter, although the Latin ones were not yet over). One missing line is $$$p = -1$ She is also not very interesting to us. Of course, any rational point $$$(p; q)$ where $$$p \ neq -1$ corresponds to rational $$$\ alpha$ . For example, for the point $$$(2; 3)$ value $$$\ alpha = 1$ . Substitute the equation of a line into our equation and get:

$$

$$1 + p + \ alpha (p + 1) - \ alpha p (p + 1) = 0$$

Or

$$

$$1 + p + \ alpha p + \ alpha - \ alpha p ^ 2 - \ alpha p = 0$$

Or

$$

$$1 + p + \ alpha - \ alpha p ^ 2 = 0$$

Or

$$

$$\ alpha p ^ 2 - p - (1 + \ alpha) = 0$$

In the head it becomes difficult to bring members, the brain desperately asks for a piece of paper. But I lull in the hands of the baby, there is no time for paper. Run the unit test ( $$$p = 2; \ alpha = 1$ ):

$$

$$1 \ times 2 ^ 2 - 2 - (1 + 1) = 0$$

Fuf, so far so good. Now we have a quadratic equation for $$$p$ which actually should give a rational root to any rational $$$\ alpha$ . How can this be, is there a discriminant and all that? Okay, let's try:

$$

$$D = b ^ 2 - 4 a c = 1 ^ 2 + 4 \ alpha (1 + \ alpha) = 1 + 4 \ alpha + 4 \ alpha ^ 2 = (1 + 2 \ alpha) ^ 2$$

Oh, oh, well, like, a full square came out. Endorphin went to the brain. He, a kind of drug addict, seemed to be seeking this. Here it is the magic of mathematics: a rational number had to come out and work out. We recall the formula for the roots:

$$

$$p_ {1,2} = \ frac {-b \ pm \ sqrt D} {2 a}$$

Or in our notation:

$$

$$p_1 = \ frac {1 - (1 + 2 \ alpha)} {2 \ alpha} = -1$$

$$

$$p_2 = \ frac {1 + (1 + 2 \ alpha)} {2 \ alpha} = \ frac {1 + \ alpha} \ alpha$$

$$$p_1$ - this is our pivot point $$$-1$ it is not interesting to us. Our solution is $$$p_2$ . Substituting it into $$$q = \ alpha (p + 1)$ we get the answer:

$$

$$p = \ frac {1 + \ alpha} \ alpha; q = 1 + 2 \ alpha$$

That is, you just need to sort out all the rational fractions as $$$\ alpha$ and for them we get all rational solutions of the equation $$$1 + p + q - pq = 0$ (well, except for some that are not very interesting to us).

Of course, it is easier to sort integers, not rational ones. Soldering the baby simethicone, I substitute $$$\ alpha = m / n$ and get:

$$

$$p = \ frac {1 + \ frac m n} {\ frac m n} = \ frac {n + m} m$$

$$

$$q = 2 + \ frac m n = \ frac {n + 2m} n$$

(God, brain, why did you choose $$$m$ and $$$n$ ? They are so easily confused in the head! Are there few letters?) In our unit test, if $$$\ alpha = 1$ then fit $$$m = n = 1$ and it's easy to make sure the test passes.

How do we get back to integers? Remember that we replaced $$$p = a / x; q = b / x$ . So, we must take for $$$x$ any number multiple to a common denominator from formulas above. In particular, fits just $$$mn$ . As a result, we have:

$$

$$x = mn; a = mn + n ^ 2; b = mn + 2m ^ 2$$

It is seen that if $$$m$ and $$$n$ not mutually simple, then the solution will be a multiple of their common divisor, so we are only interested in mutually simple $$$m$ and $$$n$ . The multiple solution will also work if $$$n$ will be even. In fact let $$$n = 2n '$ . Then

$$

$$x = 2mn '; a = 2mn '+ 4n' ^ 2; b = 2mn '+ 2m ^ 2$$

If you divide everything by two, we get

$$

$$x = mn '; a = mn '+ 2n' ^ 2; b = mn '+ m ^ 2$$

This solution is symmetrical to the first, which is quite logical: after all, the problem is symmetric with respect to $$$a$ and $$$b$ . Thus, we are interested in mutually simple $$$m$ and $$$n$ , and $$$n$ is odd.

Conveniently, that expression for $$$x$ It turned out so simple. So, we have an easy way to find all non-multiple solutions for a predetermined width of the edging. $$$x$ : these are rectangles $$$a = x + n ^ 2; b = x + 2 (x / n) ^ 2$ where $$$n$ any odd divider $$$x$ mutually simple with $$$x / n$ . The next rectangle will be for $$$x = 2; n = 1; m = 2; a = 3; b = $ 1$ :

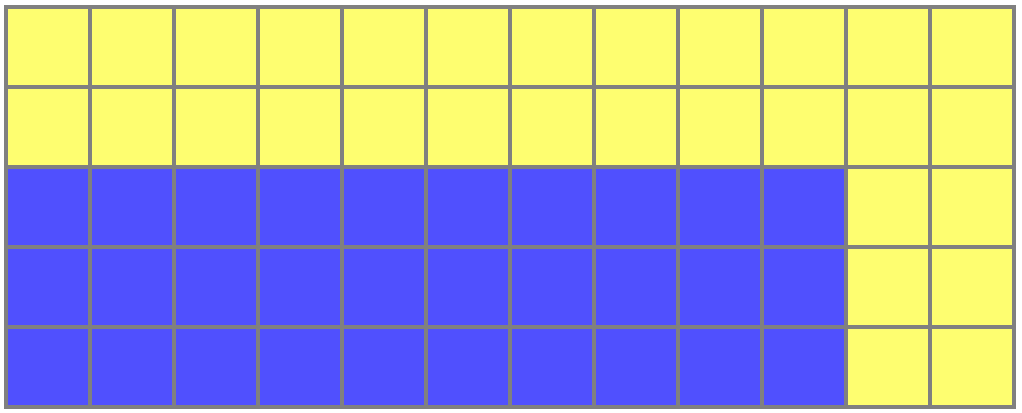
Both the blue and yellow parts contain exactly 30 cells!

Let's see what else there are solutions for small ones. $$$x$ ( $$$a$ and $$$b$ I rearranged in some places to go up):

x	n	m	area without edging	square with edging
one	one	one	2 × 3 = 6	3 × 4 = 12
2	one	2	3 × 10 = 30	5 × 12 = 60
3	one	3	4 × 21 = 84	7 × 24 = 168
3	3	one	5 × 12 = 60	8 × 15 = 120
four	one	four	5 × 36 = 180	9 × 40 = 360
five	one	five	6 × 55 = 330	11 × 60 = 660
five	five	one	7 × 30 = 210	12 × 35 = 420
6	one	6	7 × 78 = 546	13 × 84 = 1092
6	3	2	14 × 15 = 210	20 × 21 = 420

With these works in mind, the brain again achieved a dose of endorphin. How beautiful and wonderful dividers flow from one number to another! Take for example $$$6 \ times 55$ : the first is divisible by 6, and the second by 11. We add the five to both numbers, and the miracle is now the first is divisible by 11, and the second is by 6. And such tricks in every line! And then the son seemed to calm down. Eleven in the evening, you can go to bed.

Perhaps this can all be considered easier. Perhaps my reasoning was somewhere inaccurate. Perhaps these numbers and works have some special name. I do not know - not looking. I am more interested in this: I am just occupying my mind with such nonsense, or you, too, are suffering are you enjoying? Will they cure us?