An overview of the new UMAP dimension reduction algorithm. Is it really better and faster than t-sne?
Hi, Habr! The task of reducing the dimension is one of the most important in data analysis and may arise in the following two cases. First, for visualization purposes: before working with multidimensional data, it may be useful for a researcher to look at their structure, reducing the dimension and projecting it onto a two-dimensional or three-dimensional plane. Secondly, lowering the dimension is useful for preprocessing signs in machine learning models, since it is often inconvenient to train algorithms on a hundred signs, among which there may be a lot of noisy and / or linearly dependent ones, of course we would like to get rid of them. Finally, reducing the dimension of space speeds up the training of models, and we all know that time is our most valuable resource.
UMAP (Uniform Manifold Approximation and Projection) is a new dimension reduction algorithm, the library with the implementation of which was released quite recently. The authors of the algorithm believe that UMAP is able to challenge modern models of reducing the dimension, in particular, t-SNE, which is by far the most popular. According to the results of their research, UMAP has no restrictions on the dimension of the original feature space, which needs to be reduced, it is much faster and more computationally efficient than t-SNE, and it also copes better with the task of transferring the global data structure to a new, reduced space.
In this article, we will try to make out what UMAP is, how to set up an algorithm, and finally, check whether it really has advantages over t-SNE.
')

Algorithms for reducing the dimension can be divided into 2 main groups: they are trying to maintain either a global data structure or local distances between points. The first includes such algorithms as the Principal Component Method (PCA) and MDS (Multidimensional Scaling) , and the second includes t-SNE , ISOMAP , LargeVis, and others. UMAP refers to the latter and shows results similar to t-SNE.
Since a deep mathematical preparation, knowledge of Riemannian geometry and topology is required for a deep understanding of the principles of the algorithm, we describe only the general idea of the UMAP model, which can be divided into two main steps. At the first stage, we estimate the space in which, by our assumption, there are data. It can be set a priori (how simple ), or estimate based on data. And in the second step we are trying to create a mapping from the estimated space at the first stage to a new, smaller dimension.
So, now we will try to apply UMAP to any data set and compare its visualization quality with t-SNE. Our choice fell on dataset Fashion MNIST , which includes 70,000 black and white images of various clothes in 10 classes: T-shirts, pants, sweaters, dresses, sneakers, etc. Each picture has a size of 28x28 pixels or 784 pixels in total. They will be features in our model.
So, let's try to use the UMAP library in Python in order to present our garments on a two-dimensional plane. Set the number of neighbors, equal to 5, and leave the remaining parameters by default. We will discuss them later.
The result of the transformation was two vectors of the same length as the original dataset. Visualize these vectors and see how well the algorithm was able to preserve the data structure:
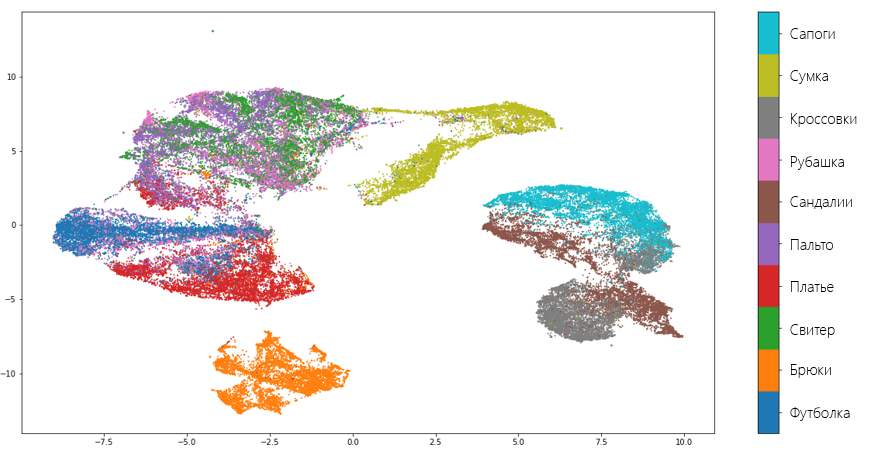
As you can see, the algorithm copes quite well and "has not lost" most of the valuable information that distinguishes one type of clothing from another. Also, the fact that the UMAP has separated shoes, clothing for the body and pants from each other also speaks about the quality of the algorithm, understanding that these are completely different things. Of course, there are mistakes. For example, the model decided that a shirt and a sweater are one and the same.
Now let's see how t-SNE is managed with the same data set. To do this, we will use Multicore TSNE — the fastest (even in single-core mode) among all implementations of the algorithm:
Result:
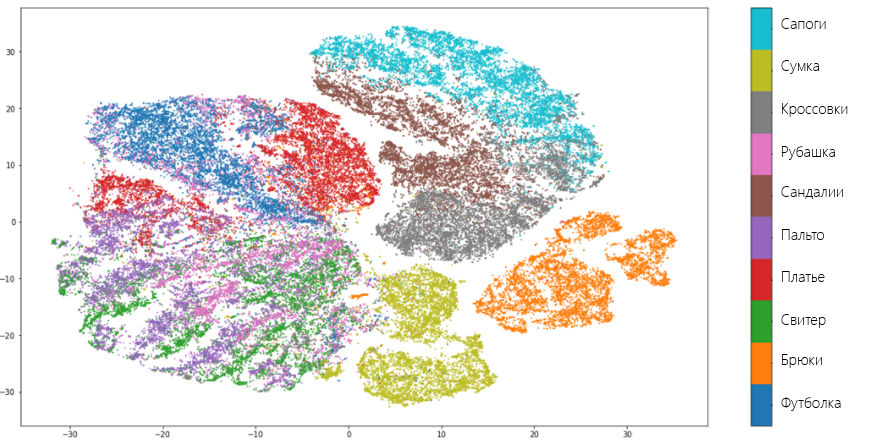
T-SNE shows similar results with UMAP and makes the same mistakes. However, unlike UMAP, t-SNE does not so clearly combine the types of clothing into separate groups: pants, things for the body and for legs are close to each other. However, in general, it can be said that both algorithms have coped with the task equally well and the researcher is free to choose between one or the other. It was possible, if not for one "but."
This “but” is the speed of learning. On a server with 4 Intel Xeon E5-2690v3 cores, 2.6 Hz and 16 GB of RAM on a 70000x784 data set, the UMAP learned in 4 minutes and 21 seconds , while it took t-SNE almost 5 times longer : 20 minutes, 14 seconds . That is, UMAP is much more computationally efficient, which gives it a huge advantage over other algorithms, including t-SNE.
The number of neighbors is n_neighbors . Varying this parameter, you can choose what is more important to save in the new spatial representation of the data: global or local data structure. Small parameter values mean that, trying to estimate the space in which data is distributed, the algorithm is limited to a small neighborhood around each point, that is, it tries to catch a local data structure (possibly to the detriment of the overall picture). On the other hand, the large values of the n_neighbors force UMAP to take into account points in a larger neighborhood, keeping the global data structure, but missing details.
Let's look at the example of our dataset, how the n_neighbors parameter affects the quality and speed of training:
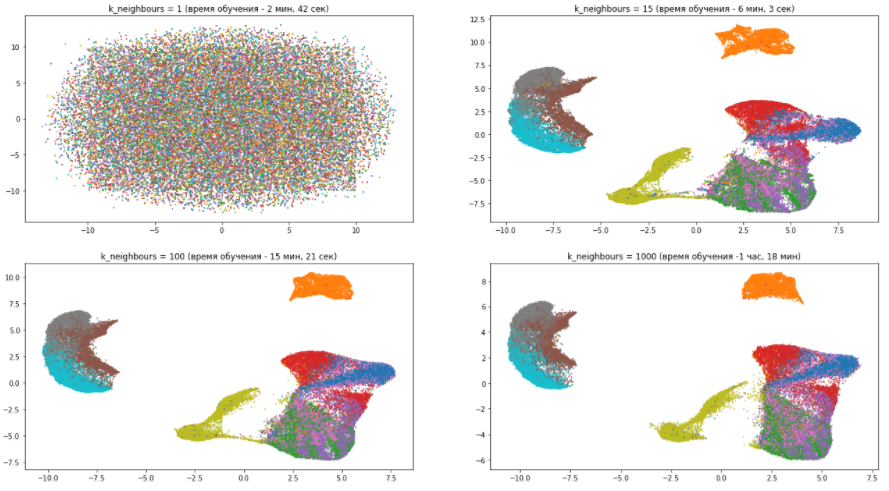
From this picture we can draw the following several conclusions:
The minimum distance is min_dist . This parameter should be understood literally: it determines the minimum distance at which points in the new space can be located. Low values should be used if you are interested in which clusters your data is divided into, and high values if it is more important for you to look at the data structure as a whole.
Let's return to our dataset and estimate the effect of the min_dist parameter. The value of n_neighbors will be fixed and equal to 5:
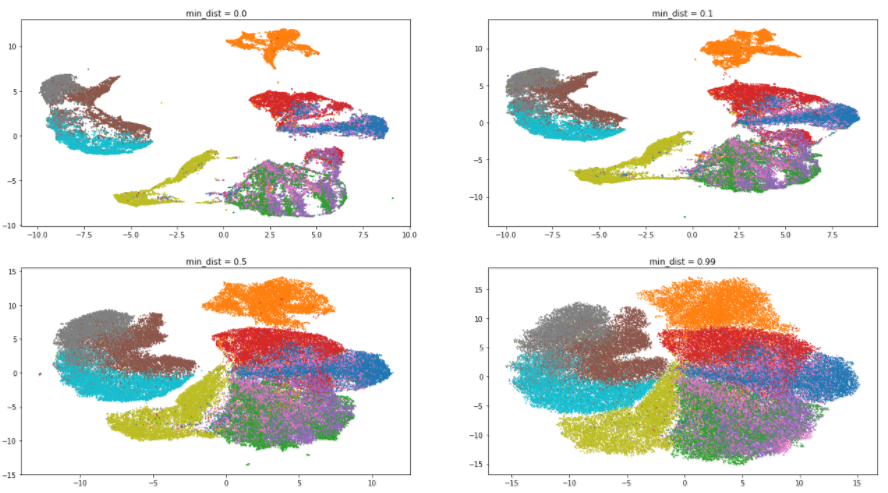
As expected, increasing the value of the parameter leads to a lesser degree of clustering, data is collected in a heap and the differences between them are erased. Interestingly, with the minimum value of min_dist, the algorithm tries to find differences within the clusters and divide them into even smaller groups.
Distance metric - metric . The metric parameter determines how distances in the source data space will be calculated. By default, the UMAP supports all possible distances, from Minkowski to Hamming. The choice of metric depends on how we interpret this data and its type. For example, when working with textual information, it is preferable to use the cosine distance ( metric = 'cosine' ).
Let's continue to play with our dataset and try various metrics:
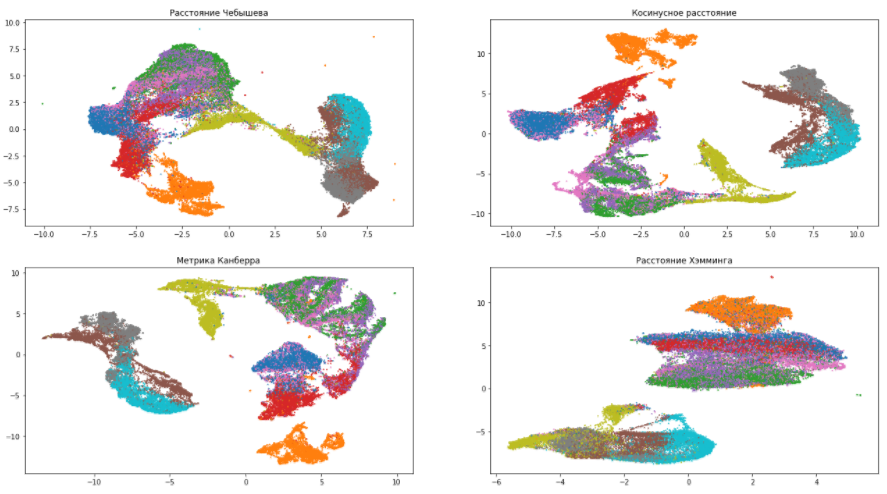
According to the pictures, you can make sure that the choice of the distance measure greatly influences the final result, therefore, its choice should be approached responsibly. If you are not sure which metric of the variety to choose, then the Euclidean distance is the safest option (the default is in UMAP).
The dimension of the finite space is n_components . Everything is obvious here: the parameter determines the dimension of the final space. If you need to visualize data, then you should choose 2 or 3. If you use transformed vectors as features of machine learning models, then more is possible.
UMAP was developed quite recently and is constantly being improved, but now we can say that it is not inferior to other algorithms in terms of the quality of work and may finally solve the main problem of modern models of dimension reduction - slowness of learning.
Finally, see how UMAP was able to visualize the Google News data set, consisting of 3 million word vectors. The training time was 200 minutes, while it took several days for t-SNE:

By the way, the drawing was built using the datashader library for visualizing big data, which we will tell you about in one of the following articles!
Among the algorithms for reducing the dimension is SVD, to which we pay attention in the context of building recommendations on our program “Big Data Specialist 8.0” , which starts already on March 22.
UMAP (Uniform Manifold Approximation and Projection) is a new dimension reduction algorithm, the library with the implementation of which was released quite recently. The authors of the algorithm believe that UMAP is able to challenge modern models of reducing the dimension, in particular, t-SNE, which is by far the most popular. According to the results of their research, UMAP has no restrictions on the dimension of the original feature space, which needs to be reduced, it is much faster and more computationally efficient than t-SNE, and it also copes better with the task of transferring the global data structure to a new, reduced space.
In this article, we will try to make out what UMAP is, how to set up an algorithm, and finally, check whether it really has advantages over t-SNE.
')

Some theory
Algorithms for reducing the dimension can be divided into 2 main groups: they are trying to maintain either a global data structure or local distances between points. The first includes such algorithms as the Principal Component Method (PCA) and MDS (Multidimensional Scaling) , and the second includes t-SNE , ISOMAP , LargeVis, and others. UMAP refers to the latter and shows results similar to t-SNE.
Since a deep mathematical preparation, knowledge of Riemannian geometry and topology is required for a deep understanding of the principles of the algorithm, we describe only the general idea of the UMAP model, which can be divided into two main steps. At the first stage, we estimate the space in which, by our assumption, there are data. It can be set a priori (how simple ), or estimate based on data. And in the second step we are trying to create a mapping from the estimated space at the first stage to a new, smaller dimension.
Application results
So, now we will try to apply UMAP to any data set and compare its visualization quality with t-SNE. Our choice fell on dataset Fashion MNIST , which includes 70,000 black and white images of various clothes in 10 classes: T-shirts, pants, sweaters, dresses, sneakers, etc. Each picture has a size of 28x28 pixels or 784 pixels in total. They will be features in our model.
So, let's try to use the UMAP library in Python in order to present our garments on a two-dimensional plane. Set the number of neighbors, equal to 5, and leave the remaining parameters by default. We will discuss them later.
import pandas as pd import umap fmnist = pd.read_csv('fashion-mnist.csv') # embedding = umap.UMAP(n_neighbors=5).fit_transform(fmnist.drop('label', axis=1)) # The result of the transformation was two vectors of the same length as the original dataset. Visualize these vectors and see how well the algorithm was able to preserve the data structure:

As you can see, the algorithm copes quite well and "has not lost" most of the valuable information that distinguishes one type of clothing from another. Also, the fact that the UMAP has separated shoes, clothing for the body and pants from each other also speaks about the quality of the algorithm, understanding that these are completely different things. Of course, there are mistakes. For example, the model decided that a shirt and a sweater are one and the same.
Now let's see how t-SNE is managed with the same data set. To do this, we will use Multicore TSNE — the fastest (even in single-core mode) among all implementations of the algorithm:
from MulticoreTSNE import MulticoreTSNE as TSNE tsne = TSNE() embedding_tsne = tsne.fit_transform(fmnist.drop('label', axis = 1)) Result:

T-SNE shows similar results with UMAP and makes the same mistakes. However, unlike UMAP, t-SNE does not so clearly combine the types of clothing into separate groups: pants, things for the body and for legs are close to each other. However, in general, it can be said that both algorithms have coped with the task equally well and the researcher is free to choose between one or the other. It was possible, if not for one "but."
This “but” is the speed of learning. On a server with 4 Intel Xeon E5-2690v3 cores, 2.6 Hz and 16 GB of RAM on a 70000x784 data set, the UMAP learned in 4 minutes and 21 seconds , while it took t-SNE almost 5 times longer : 20 minutes, 14 seconds . That is, UMAP is much more computationally efficient, which gives it a huge advantage over other algorithms, including t-SNE.
Algorithm parameters
The number of neighbors is n_neighbors . Varying this parameter, you can choose what is more important to save in the new spatial representation of the data: global or local data structure. Small parameter values mean that, trying to estimate the space in which data is distributed, the algorithm is limited to a small neighborhood around each point, that is, it tries to catch a local data structure (possibly to the detriment of the overall picture). On the other hand, the large values of the n_neighbors force UMAP to take into account points in a larger neighborhood, keeping the global data structure, but missing details.
Let's look at the example of our dataset, how the n_neighbors parameter affects the quality and speed of training:

From this picture we can draw the following several conclusions:
- With a number of neighbors equal to one, the algorithm works just awful, because it focuses too much on details and simply cannot catch the overall data structure.
- With the growing number of neighbors, the model pays less attention to the differences between different types of clothing, grouping similar ones and mixing them together. At the same time, completely different wardrobe items are getting farther from each other. As already mentioned, the overall picture becomes clearer, and the details are blurred.
- The n_neighbors parameter significantly affects the training time. so you need to carefully approach his selection.
The minimum distance is min_dist . This parameter should be understood literally: it determines the minimum distance at which points in the new space can be located. Low values should be used if you are interested in which clusters your data is divided into, and high values if it is more important for you to look at the data structure as a whole.
Let's return to our dataset and estimate the effect of the min_dist parameter. The value of n_neighbors will be fixed and equal to 5:

As expected, increasing the value of the parameter leads to a lesser degree of clustering, data is collected in a heap and the differences between them are erased. Interestingly, with the minimum value of min_dist, the algorithm tries to find differences within the clusters and divide them into even smaller groups.
Distance metric - metric . The metric parameter determines how distances in the source data space will be calculated. By default, the UMAP supports all possible distances, from Minkowski to Hamming. The choice of metric depends on how we interpret this data and its type. For example, when working with textual information, it is preferable to use the cosine distance ( metric = 'cosine' ).
Let's continue to play with our dataset and try various metrics:

According to the pictures, you can make sure that the choice of the distance measure greatly influences the final result, therefore, its choice should be approached responsibly. If you are not sure which metric of the variety to choose, then the Euclidean distance is the safest option (the default is in UMAP).
The dimension of the finite space is n_components . Everything is obvious here: the parameter determines the dimension of the final space. If you need to visualize data, then you should choose 2 or 3. If you use transformed vectors as features of machine learning models, then more is possible.
Conclusion
UMAP was developed quite recently and is constantly being improved, but now we can say that it is not inferior to other algorithms in terms of the quality of work and may finally solve the main problem of modern models of dimension reduction - slowness of learning.
Finally, see how UMAP was able to visualize the Google News data set, consisting of 3 million word vectors. The training time was 200 minutes, while it took several days for t-SNE:

By the way, the drawing was built using the datashader library for visualizing big data, which we will tell you about in one of the following articles!
Among the algorithms for reducing the dimension is SVD, to which we pay attention in the context of building recommendations on our program “Big Data Specialist 8.0” , which starts already on March 22.
Source: https://habr.com/ru/post/350584/
All Articles