Asynchronous (self-timed) circuits. Calculation of logical functions directly on the event graph. Part 2
Let me remind you that in the first part it was about calculating simple implicants (conjunctions) for cyclic behaviors without parallelism, selection and multiple signals at three points (states).

The task was that the implicant covered point 2 (that is, was equal to 1 on this state) and did not go beyond the limits indicated by points 1 and 3 ... At the same time, the position of the left border of implicants (to the left of point 2) is indifferent. The right border (to the right of point 2) should be as much as possible shifted to the right. The impossibility of calculating implicants means the presence of a CSC conflict. That is, there is a continuous sequence of events (but not the entire behavior), in which each signal is switched an even number of times.
')
We now proceed to the calculation of the minimum logical function (DNF) for the signal x.
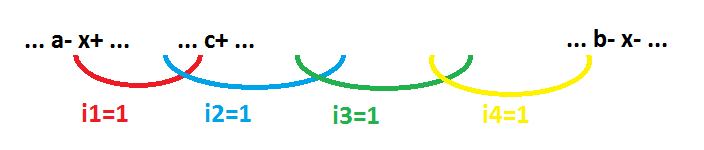
To build a function for signal x means to cover all states with implicants, where the function of signal x is 1. In this example, this is a sequence of states that begins immediately after event a- and ends immediately before event b-. Implicants are indicated by colored arcs. At the same time, no implicant should cover the state where the signal function x is equal to 0. Let me remind you that by implicant we mean the set of states where it is 1. In this example, we get a non-inverting function (AND-OR). If the implicants overlap the space from "-" events to "+" events (in the direction of the process unfolding), then we get an inverting function (AND-OR-NOT). Another important note. Since the logic function is calculated for the element of the self-timed circuit, neighboring implicants must intersect, that is, they must have at least one common state.
The algorithm for calculating the minimum function is as follows. When specifying the location of the computed implicants as point 1, we will always use the point to the right of the a- event (in the figure). And as point 3 we will always use the point to the left of the b- event (in the figure). Implicants will be calculated sequentially one after the other in the direction from the x + event to the x- event. First red, then blue, then green and so on (in the picture). This is due to the simple implicants calculation algorithm used.
Step 1. As point 2, select the point located to the left of the x + event (in the figure).
Step 2. Calculate the implicant from the given three points. The resulting implicant is included in the final function record.
Comment. If several alternative implicants are received, then each option of including the alternative implicant in the final record of the function should be considered. Accordingly, for each variant, the calculations must be continued separately.
Step 3. Consider the right boundary of the newly computed implicants. In the figure, this is a c + event (for the first computed implicants). If the right border of the implicants is the immediate cause of the x- event, it means that the function has been calculated, we exit the algorithm.
Step 4. For point 2, select the point located to the left of the right border of the last computed implicants. Go to step 2.
This algorithm assumes that the form of the minimal function is not defined. But for the model currently being considered, the minimum function of any signal can be written as follows:
one)
Is an implicant consisting of one or more variables. - this is probably an empty implicant set consisting of one variable. - This is an implicant of 2 variables, the presence of which in the minimum form is not required. All variables, except x, can be included in the formula both in direct and inverse form, depending on the arrangement of signs of the corresponding events. All variables are included in the formula as arguments strictly once.
Indeed, consider the possible location of the first computed implicants. There are two such options. The first, when the right border of the implicants is the cause of the x- event:

In this case, the implicant covers all states on which the function x is equal to 1. The function looks like this: x = a * b * c. In the following, we will use only its borders to denote implicants. In this example, these are a + and c- (left and right borders, respectively). All event signs (except for x switchings) are conditional and can be replaced with the opposite. They are only intended to distinguish events with the same name.
The second variant of the location of the implicants - the right border of the implicants is not the direct cause of the x- event:

In this case, the signal f, “-” whose switching is the direct cause of the x- event, can be arranged in three different ways.
The first variant of the location of the f + event is between the x- and a + events (as the process unfolds):

In this case, the second implicant cannot consist of one variable. But the implicant f * x covers all the remaining uncovered states on which the function x is equal to 1. The position of the event f + corresponds to the formula x = a * b * c + f * x.
The second arrangement of the f + event is between the x + and c- events:
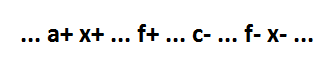
In this case, the second and last implicant consists of one variable f, which corresponds to the formula x = a * b * c + f.
The third option is the location of the event f + - between the events c- and f-:
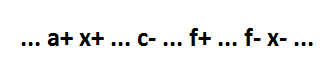
In this case, as in the previous one, the implicant f must necessarily be part of the minimal function. Only in this case this implicants are not enough to complete the construction of the function. Consider some event g-, located between the events f + and f-. Such an event must necessarily be, otherwise it would mean a CSC conflict.
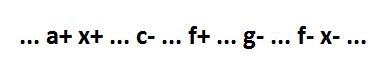
For event g + 4 location options. The first option for the location of the g + event is between the x + and c- events:
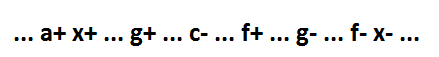
In this case, implicants g is enough to complete the construction of a minimal function that looks like x = a * b * c + f + g.
If there is no g + event located between the x + and c- events, consider the second variant of the location of the g + event between the x- and a + events:

In this case there is no third implicants, consisting of one variable, otherwise it would be the first option for the location of the event g +. But the implicants g * x are enough to complete the calculation of the minimum function. The formula looks like this: x = a * b * c + f + g * x.
The third option. If for any signal g the event g + is located between the events f + and f-. This means CSC conflict.

There is a fourth option. The g + event is located between the c- and f + events.
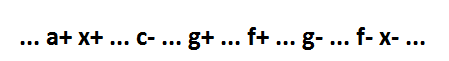
Since there are no such signals g that would satisfy the first or second variant of the location of the event g +, an implicant consisting of one variable g must necessarily enter the minimum form.
Next, consider a signal h, the switching of which is located between the events g + and f +.
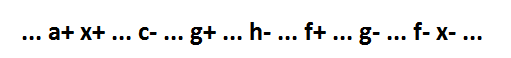
And consider the options for the location of the event h + as well as it did for the event g +. In the end, we will either find a CSC conflict, or obtain formula 1).
What does this formula give? The first. The signals f, g, h, i from the formula form a chain of interceptions and are essentially implicant. Thus, the calculation of the minimum function is reduced to finding two implicants. Only setting the conditions for the search is somewhat different from what was said above. The complexity of the algorithm for calculating in the limit is quadratic with respect to the number of signals. But the quadratic component has negligible weight. Therefore, we can talk about linear complexity. Well, in addition, the algorithm requires almost no memory.
Second moment. Such a recording of the minimal function allows one to make decomposition to arbitrarily small elements without breaking self-synchronization. Consider the function x = a * b + f + g + h * x. Its behavior looks like this:
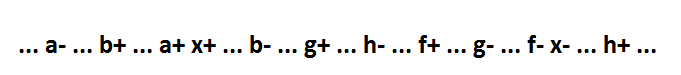
Such a function cannot be fully decomposed. This flaw is corrected by adding the signal y:

Now the functions look like this: x = (f + g + h) * y, y = a * b + x. In order to preserve self-synchronization, it remains to replace the argument of the signal function, the cause of which switching was the x- event: we change it to y.
Consider the function x = a * b * c + f + g. Her behavior:
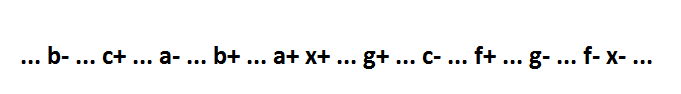
For such a function, you can always, without losing self-synchronization, select the first implicant as a separate element: y = a * b * c, x = y + g + f. The behavior with the new element will be as follows:
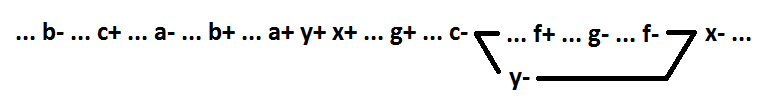
Looking ahead, I had to use parallelism. More on this further. It remains to consider a function of the form x = a * b * c * d. Her behavior:
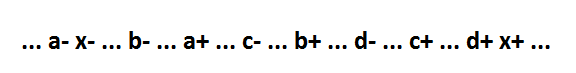
In such a function, you can always select the first variables as a separate element without loss of self-synchronization (for example, a, b, c): y = a * b * c, x = y * d. Behavior with new item:
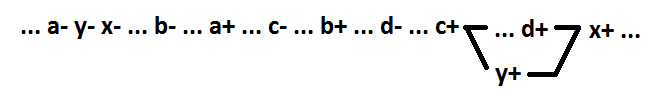
Using these three transformations, you can split the logic elements to the required level.
The question remains: how much does all this have practical value? After all, a very limited model is being considered. In the future, I will show that for any behavior, using linear complexity transformations (adding new signals), the calculation of the logical function for any signal can be reduced to the search for two implicants. And the resulting function can be split up to the required level. To be continued.

The task was that the implicant covered point 2 (that is, was equal to 1 on this state) and did not go beyond the limits indicated by points 1 and 3 ... At the same time, the position of the left border of implicants (to the left of point 2) is indifferent. The right border (to the right of point 2) should be as much as possible shifted to the right. The impossibility of calculating implicants means the presence of a CSC conflict. That is, there is a continuous sequence of events (but not the entire behavior), in which each signal is switched an even number of times.
')
We now proceed to the calculation of the minimum logical function (DNF) for the signal x.

To build a function for signal x means to cover all states with implicants, where the function of signal x is 1. In this example, this is a sequence of states that begins immediately after event a- and ends immediately before event b-. Implicants are indicated by colored arcs. At the same time, no implicant should cover the state where the signal function x is equal to 0. Let me remind you that by implicant we mean the set of states where it is 1. In this example, we get a non-inverting function (AND-OR). If the implicants overlap the space from "-" events to "+" events (in the direction of the process unfolding), then we get an inverting function (AND-OR-NOT). Another important note. Since the logic function is calculated for the element of the self-timed circuit, neighboring implicants must intersect, that is, they must have at least one common state.
The algorithm for calculating the minimum function is as follows. When specifying the location of the computed implicants as point 1, we will always use the point to the right of the a- event (in the figure). And as point 3 we will always use the point to the left of the b- event (in the figure). Implicants will be calculated sequentially one after the other in the direction from the x + event to the x- event. First red, then blue, then green and so on (in the picture). This is due to the simple implicants calculation algorithm used.
Step 1. As point 2, select the point located to the left of the x + event (in the figure).
Step 2. Calculate the implicant from the given three points. The resulting implicant is included in the final function record.
Comment. If several alternative implicants are received, then each option of including the alternative implicant in the final record of the function should be considered. Accordingly, for each variant, the calculations must be continued separately.
Step 3. Consider the right boundary of the newly computed implicants. In the figure, this is a c + event (for the first computed implicants). If the right border of the implicants is the immediate cause of the x- event, it means that the function has been calculated, we exit the algorithm.
Step 4. For point 2, select the point located to the left of the right border of the last computed implicants. Go to step 2.
This algorithm assumes that the form of the minimal function is not defined. But for the model currently being considered, the minimum function of any signal can be written as follows:
one)
Is an implicant consisting of one or more variables. - this is probably an empty implicant set consisting of one variable. - This is an implicant of 2 variables, the presence of which in the minimum form is not required. All variables, except x, can be included in the formula both in direct and inverse form, depending on the arrangement of signs of the corresponding events. All variables are included in the formula as arguments strictly once.
Indeed, consider the possible location of the first computed implicants. There are two such options. The first, when the right border of the implicants is the cause of the x- event:

In this case, the implicant covers all states on which the function x is equal to 1. The function looks like this: x = a * b * c. In the following, we will use only its borders to denote implicants. In this example, these are a + and c- (left and right borders, respectively). All event signs (except for x switchings) are conditional and can be replaced with the opposite. They are only intended to distinguish events with the same name.
The second variant of the location of the implicants - the right border of the implicants is not the direct cause of the x- event:

In this case, the signal f, “-” whose switching is the direct cause of the x- event, can be arranged in three different ways.
The first variant of the location of the f + event is between the x- and a + events (as the process unfolds):

In this case, the second implicant cannot consist of one variable. But the implicant f * x covers all the remaining uncovered states on which the function x is equal to 1. The position of the event f + corresponds to the formula x = a * b * c + f * x.
The second arrangement of the f + event is between the x + and c- events:
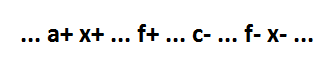
In this case, the second and last implicant consists of one variable f, which corresponds to the formula x = a * b * c + f.
The third option is the location of the event f + - between the events c- and f-:
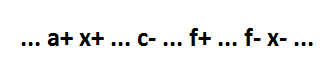
In this case, as in the previous one, the implicant f must necessarily be part of the minimal function. Only in this case this implicants are not enough to complete the construction of the function. Consider some event g-, located between the events f + and f-. Such an event must necessarily be, otherwise it would mean a CSC conflict.
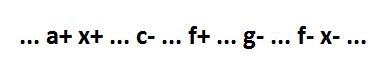
For event g + 4 location options. The first option for the location of the g + event is between the x + and c- events:
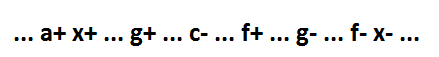
In this case, implicants g is enough to complete the construction of a minimal function that looks like x = a * b * c + f + g.
If there is no g + event located between the x + and c- events, consider the second variant of the location of the g + event between the x- and a + events:

In this case there is no third implicants, consisting of one variable, otherwise it would be the first option for the location of the event g +. But the implicants g * x are enough to complete the calculation of the minimum function. The formula looks like this: x = a * b * c + f + g * x.
The third option. If for any signal g the event g + is located between the events f + and f-. This means CSC conflict.

There is a fourth option. The g + event is located between the c- and f + events.
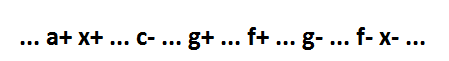
Since there are no such signals g that would satisfy the first or second variant of the location of the event g +, an implicant consisting of one variable g must necessarily enter the minimum form.
Next, consider a signal h, the switching of which is located between the events g + and f +.
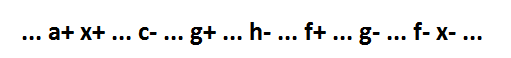
And consider the options for the location of the event h + as well as it did for the event g +. In the end, we will either find a CSC conflict, or obtain formula 1).
What does this formula give? The first. The signals f, g, h, i from the formula form a chain of interceptions and are essentially implicant. Thus, the calculation of the minimum function is reduced to finding two implicants. Only setting the conditions for the search is somewhat different from what was said above. The complexity of the algorithm for calculating in the limit is quadratic with respect to the number of signals. But the quadratic component has negligible weight. Therefore, we can talk about linear complexity. Well, in addition, the algorithm requires almost no memory.
Second moment. Such a recording of the minimal function allows one to make decomposition to arbitrarily small elements without breaking self-synchronization. Consider the function x = a * b + f + g + h * x. Its behavior looks like this:
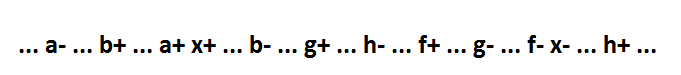
Such a function cannot be fully decomposed. This flaw is corrected by adding the signal y:

Now the functions look like this: x = (f + g + h) * y, y = a * b + x. In order to preserve self-synchronization, it remains to replace the argument of the signal function, the cause of which switching was the x- event: we change it to y.
Consider the function x = a * b * c + f + g. Her behavior:
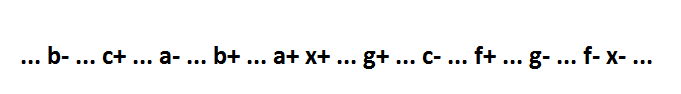
For such a function, you can always, without losing self-synchronization, select the first implicant as a separate element: y = a * b * c, x = y + g + f. The behavior with the new element will be as follows:
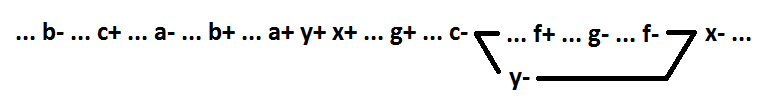
Looking ahead, I had to use parallelism. More on this further. It remains to consider a function of the form x = a * b * c * d. Her behavior:
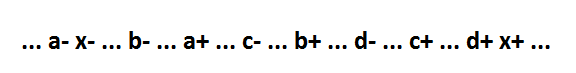
In such a function, you can always select the first variables as a separate element without loss of self-synchronization (for example, a, b, c): y = a * b * c, x = y * d. Behavior with new item:
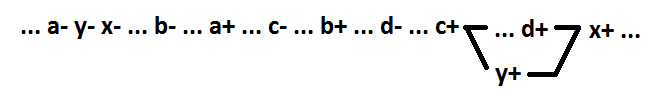
Using these three transformations, you can split the logic elements to the required level.
The question remains: how much does all this have practical value? After all, a very limited model is being considered. In the future, I will show that for any behavior, using linear complexity transformations (adding new signals), the calculation of the logical function for any signal can be reduced to the search for two implicants. And the resulting function can be split up to the required level. To be continued.
Source: https://habr.com/ru/post/350560/
All Articles