Work with Anaconda on the example of searching for the correlation of cryptocurrency rates

The purpose of this article is to provide an easy introduction to data analysis using Anaconda. We will go through writing a simple Python script to extract, analyze and visualize data on various cryptocurrencies.

Step 1 - Setting up the work environment.

The only skills you need are a basic understanding of Python.

Step 1.1 - Install Anaconda
')
Anaconda distribution can be downloaded from the official website .
Installation takes place in standard Step-by-Step mode.

Step 1.2 - Setting up the project work environment

After Anaconda is installed, you need to create and activate a new environment to organize our dependencies.

Why use a medium? If you plan to develop several Python projects on your computer, it is useful to store dependencies (software libraries and packages) separately to avoid conflicts. Anaconda will create a special environment directory for the dependencies of each project, so that everything is organized and shared.

This can be done either via the command line

conda create --name cryptocurrency-analysis python=3.6 

 source activate cryptocurrency-analysis 

(Linux / macOS)

or

 activate cryptocurrency-analysis 

(Windows)

either through Anaconda Navigator



In this case, the environment is automatically activated.

Then you need to install the necessary dependencies NumPy , Pandas , nb_conda , Jupiter , Plotly , Quandl .

 conda install numpy pandas nb_conda jupyter plotly quandl 

either through Anaconda Navigator, alternately each package



This may take a few minutes.

Step 1.3 - Launch Jupyter Notebook

There is also an option via the command line jupyter notebook and open the browser at http://localhost:8888/

and through Anaconda Navigator



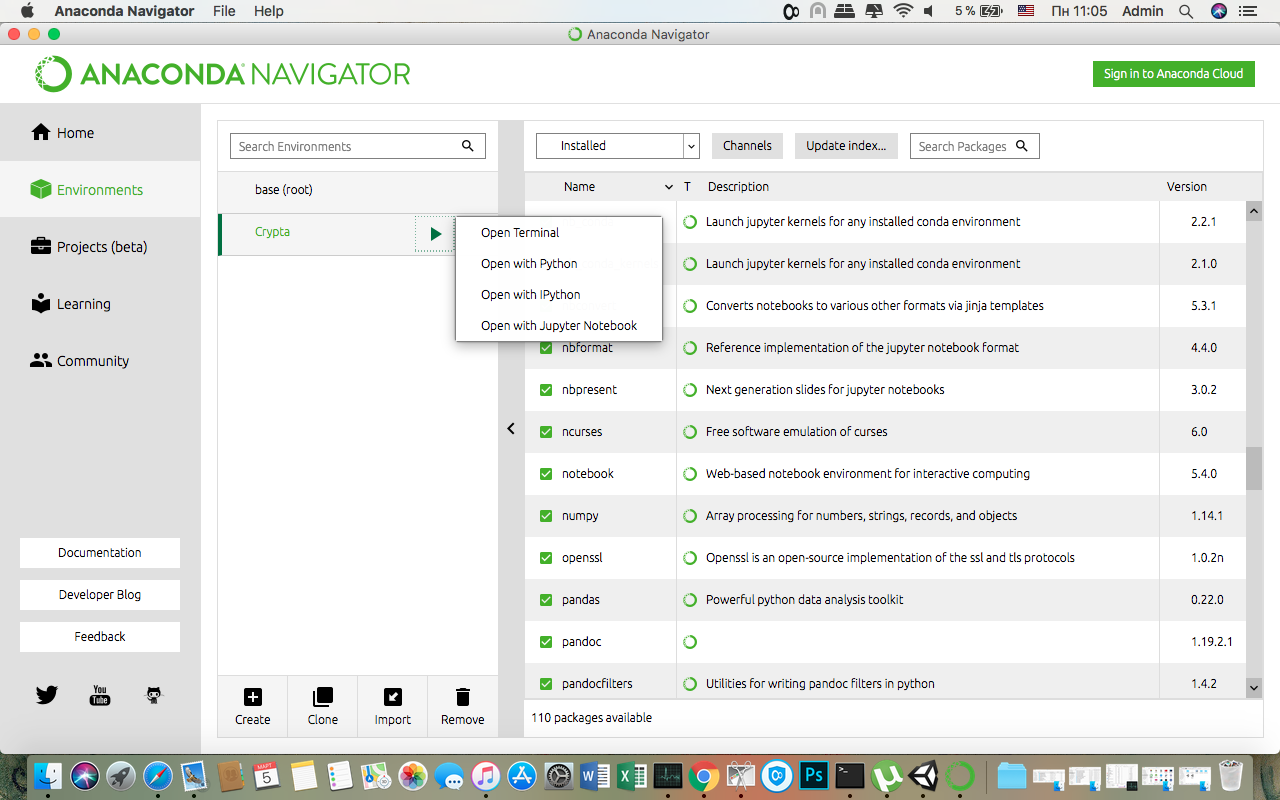
Step 1.4 - Import Dependencies

After you open an empty Jupyter Notebook, the first thing to do is import the required dependencies.

 import os import numpy as np import pandas as pd import pickle import quandl from datetime import datetime 

Then import and activate offline Plotly.

 import plotly.offline as py import plotly.graph_objs as go import plotly.figure_factory as ff py.init_notebook_mode(connected=True) 

Step 2 - Retrieving Bitcoin Pricing Data

Now that everything is set up, we are ready to begin extracting data for analysis. To begin with, we’ll get pricing data using the free Quandl API.

Step 2.1 - Define the Quandl function
To begin with, we define a function for loading and caching data sets from Quandl.

 def get_quandl_data(quandl_id): '''Download and cache Quandl dataseries''' cache_path = '{}.pkl'.format(quandl_id).replace('/','-') try: f = open(cache_path, 'rb') df = pickle.load(f) print('Loaded {} from cache'.format(quandl_id)) except (OSError, IOError) as e: print('Downloading {} from Quandl'.format(quandl_id)) df = quandl.get(quandl_id, returns="pandas") df.to_pickle(cache_path) print('Cached {} at {}'.format(quandl_id, cache_path)) return df 

We use pickle to serialize and save the loaded data as a file, which will allow our script not to reload the same data every time the script is run.

The function returns data as a pandas data set.

Step 2.2 - Getting a Bitcoin rate on the Kraken Exchange

We implement it as follows:

 btc_usd_price_kraken = get_quandl_data('BCHARTS/KRAKENUSD') 

To check the validity of the script, we can look at the first 5 lines of the response received using the head () method.

 btc_usd_price_kraken.head() 

Result:

Date	Open	High	Low	Close	Volume (BTC)	Volume (Currency)	Weighted Price
2014-01-07	874.67040	892.06753	810.00000	810.00000	15.622378	13151.472844	841.835522
2014-01-08	810.00000	899.84281	788.00000	824.98287	19.182756	16097.329584	839.156269
2014-01-09	825.56345	870.00000	807.42084	841.86934	8.158335	6784.249982	831.572913
2014-01-10	839.99000	857.34056	817.00000	857.33056	8.024510	6780.220188	844.938794
2014-01-11	858.20000	918.05471	857.16554	899.84105	18.748285	16698.566929	890.671709

And build a graph to visualize the resulting array.

 btc_trace = go.Scatter(x=btc_usd_price_kraken.index, y=btc_usd_price_kraken['Weighted Price']) py.iplot([btc_trace]) 

Here we use Plotly to generate our visualizations. This is a less traditional choice than some of the more well-known libraries, such as Matplotlib, but I think Plotly is a great choice because it creates fully interactive diagrams using D3.js.

Step 2.3 - Getting Bitcoin Rate on Multiple Exchanges

The nature of the exchange is that pricing is determined by supply and demand, therefore, no stock exchange contains the “true price” of Bitcoin. To solve this problem, we will extract additional data from three larger exchanges to calculate the total price index.

We will upload the data of each exchange to the dictionary.

 exchanges = ['COINBASE','BITSTAMP','ITBIT'] exchange_data = {} exchange_data['KRAKEN'] = btc_usd_price_kraken for exchange in exchanges: exchange_code = 'BCHARTS/{}USD'.format(exchange) btc_exchange_df = get_quandl_data(exchange_code) exchange_data[exchange] = btc_exchange_df 

Step 2.4 - Combining all prices into a single data set

Define a simple function to merge data.

 def merge_dfs_on_column(dataframes, labels, col): series_dict = {} for index in range(len(dataframes)): series_dict[labels[index]] = dataframes[index][col] return pd.DataFrame(series_dict) 

Then combine all the data on the column "Weighted Price".

 btc_usd_datasets = merge_dfs_on_column(list(exchange_data.values()), list(exchange_data.keys()), 'Weighted Price') 

Now we’ll look at the last five lines, using the tail () method to make sure everything looks fine and the way we wanted.

 btc_usd_datasets.tail() 

Result:

Date	Bitstamp	COINBASE	ITBIT	Kraken	avg_btc_price_usd
2018-02-28	10624.382893	10643.053573	10621.099426	10615.587987	10626.030970
2018-03-01	10727.272600	10710.946064	10678.156872	10671.653953	10697.007372
2018-03-02	10980.298658	10982.181881	10973.434045	10977.067909	10978.245623
2018-03-03	11332.934468	11317.108262	11294.620763	11357.539095	11325.550647
2018-03-04	11260.751253	11250.771211	11285.690725	11244.836468	11260.512414

Step 2.5 - Comparing price data sets.

The next logical step is to visualize the comparison of prices received. To do this, we define a helper function that will build a graph for each of the exchanges using Plotly.

 def df_scatter(df, title, seperate_y_axis=False, y_axis_label='', scale='linear', initial_hide=False): label_arr = list(df) series_arr = list(map(lambda col: df[col], label_arr)) layout = go.Layout( title=title, legend=dict(orientation="h"), xaxis=dict(type='date'), yaxis=dict( title=y_axis_label, showticklabels= not seperate_y_axis, type=scale ) ) y_axis_config = dict( overlaying='y', showticklabels=False, type=scale ) visibility = 'visible' if initial_hide: visibility = 'legendonly' trace_arr = [] for index, series in enumerate(series_arr): trace = go.Scatter( x=series.index, y=series, name=label_arr[index], visible=visibility ) if seperate_y_axis: trace['yaxis'] = 'y{}'.format(index + 1) layout['yaxis{}'.format(index + 1)] = y_axis_config trace_arr.append(trace) fig = go.Figure(data=trace_arr, layout=layout) py.iplot(fig) 

And call her

 df_scatter(btc_usd_datasets, '    (USD) ') 

Result:



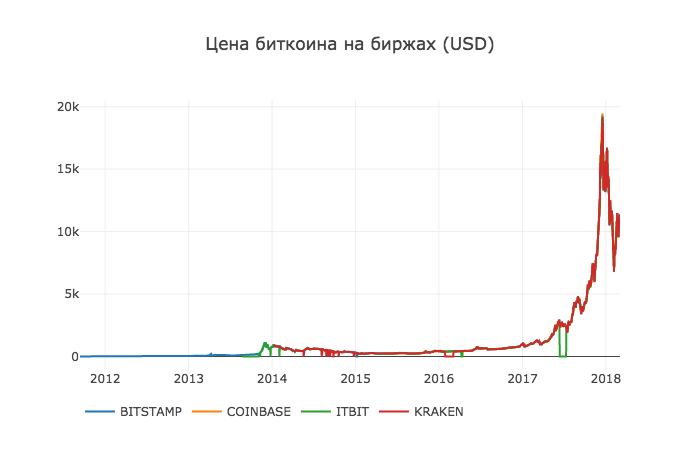
Now we will remove all zero values, since we know that the price has never been zero in the period we are considering.

 btc_usd_datasets.replace(0, np.nan, inplace=True) 

And re-create the schedule

 df_scatter(btc_usd_datasets, 'Bitcoin Price (USD) By Exchange') 

Result:



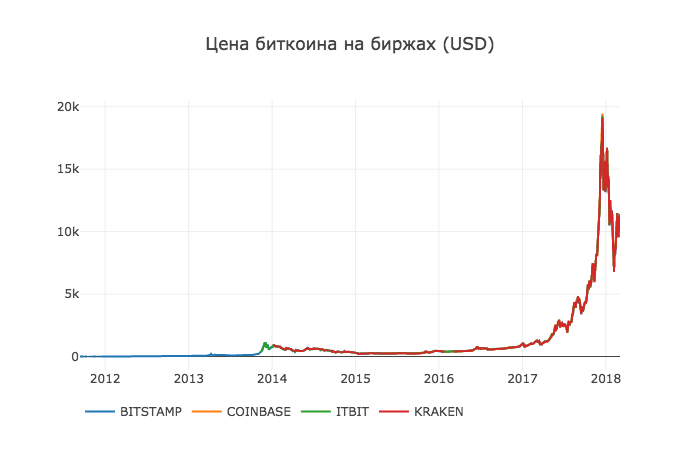
Step 2.6 - Calculate Average Price

Now we can calculate a new column containing the average daily bitcoin price on all exchanges.

 btc_usd_datasets['avg_btc_price_usd'] = btc_usd_datasets.mean(axis=1) 

This new column is our bitcoin price index. Build his schedule to make sure that he looks normal.

 btc_trace = go.Scatter(x=btc_usd_datasets.index, y=btc_usd_datasets['avg_btc_price_usd']) py.iplot([btc_trace]) 

Result:



We will use this data later to convert other cryptocurrency exchange rates to USD.

Step 3 - Acquiring data on alternative cryptocurrencies

Now that we have an array of data with Bitcoin prices, let's take some data about alternative cryptocurrencies.

Step 3.1 - Define functions for working with the Poloniex API.

We will use the Poloniex API to get the data. We define two helper functions for loading and caching JSON data from this API.

First, we define the get_json_data function, which will load and cache JSON data from the provided URL.

 def get_json_data(json_url, cache_path): try: f = open(cache_path, 'rb') df = pickle.load(f) print('Loaded {} from cache'.format(json_url)) except (OSError, IOError) as e: print('Downloading {}'.format(json_url)) df = pd.read_json(json_url) df.to_pickle(cache_path) print('Cached response at {}'.format(json_url, cache_path)) return df 

Then we define a function to format the HTTP requests for the Poloniex API and call our new function get_json_data to save the received data.

 base_polo_url = 'https://poloniex.com/public?command=returnChartData&currencyPair={}&start={}&end={}&period={}' start_date = datetime.strptime('2015-01-01', '%Y-%m-%d') end_date = datetime.now() pediod = 86400 def get_crypto_data(poloniex_pair): json_url = base_polo_url.format(poloniex_pair, start_date.timestamp(), end_date.timestamp(), pediod) data_df = get_json_data(json_url, poloniex_pair) data_df = data_df.set_index('date') return data_df 

This input function receives a pair of cryptocurrencies, for example, “BTC_ETH” and returns historical data on the exchange rate of two currencies.

Step 3.2 - Downloading data from Poloniex

Some of the alternative cryptocurrencies in question cannot be bought on exchanges directly for USD. For this reason, we will upload the bitcoin exchange rate for each of them, and then we will use the existing bitcoin pricing data to convert this value to USD.

We upload exchange data for nine popular cryptocurrencies - Ethereum , Litecoin , Ripple , Ethereum Classic , Stellar , Dash , Siacoin , Monero , and NEM .

 altcoins = ['ETH','LTC','XRP','ETC','STR','DASH','SC','XMR','XEM'] altcoin_data = {} for altcoin in altcoins: coinpair = 'BTC_{}'.format(altcoin) crypto_price_df = get_crypto_data(coinpair) altcoin_data[altcoin] = crypto_price_df 

Now we have 9 data sets, each of which contains historical average daily stock exchange ratios of bitcon to alternative cryptocurrency.

We can look at the last few lines of the Ethereum pricing table to make sure it looks normal.

 altcoin_data['ETH'].tail() 

date	close	high	low	open	quoteVolume	volume	weightedAverage
2018-03-01	0.079735	0.082911	0.079232	0.082729	17981.733693	1454.206133	0.080871
2018-03-02	0.077572	0.079719	0.077014	0.079719	18482.985554	1448.732706	0.078382
2018-03-03	0.074500	0.077623	0.074356	0.077562	15058.825646	1139.640375	0.075679
2018-03-04	0.075111	0.077630	0.074389	0.074500	12258.662182	933.480951	0.076149
2018-03-05	0.075373	0.075700	0.074723	0.075277	10993.285936	826.576693	0.075189

Step 3.3 - Price Conversion to USD.

Since we now have a bitcoin exchange rate for each cryptocurrency and we have an index of historical Bitcoin prices in USD, we can directly calculate the price in USD for each alternative cryptocurrency.

 for altcoin in altcoin_data.keys(): altcoin_data[altcoin]['price_usd'] = altcoin_data[altcoin]['weightedAverage'] * btc_usd_datasets['avg_btc_price_usd'] 

By this we have created a new column in each alternative cryptocurrency data set with prices in USD.

Then we can reuse our function merge_dfs_on_column to create a combined price data set in USD for each of the cryptocurrencies.

 combined_df = merge_dfs_on_column(list(altcoin_data.values()), list(altcoin_data.keys()), 'price_usd') 

Now add the bitcoin price to the dataset as the final column.

 combined_df['BTC'] = btc_usd_datasets['avg_btc_price_usd'] 

As a result, we have a data set containing daily prices in USD for ten cryptocurrencies, which we are considering.

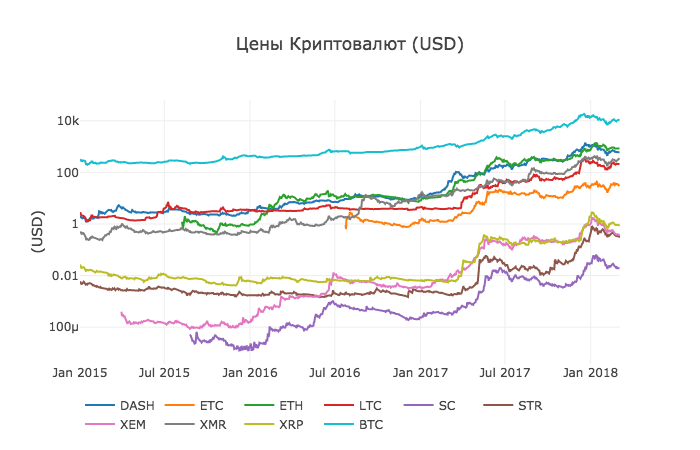
We use our df_scatter function to display all cryptocurrency prices on a chart.

 df_scatter(combined_df, '  (USD)', seperate_y_axis=False, y_axis_label='(USD)', scale='log') 

This chart provides a fairly solid "big picture" of how the exchange rates of each currency have changed over the past few years.



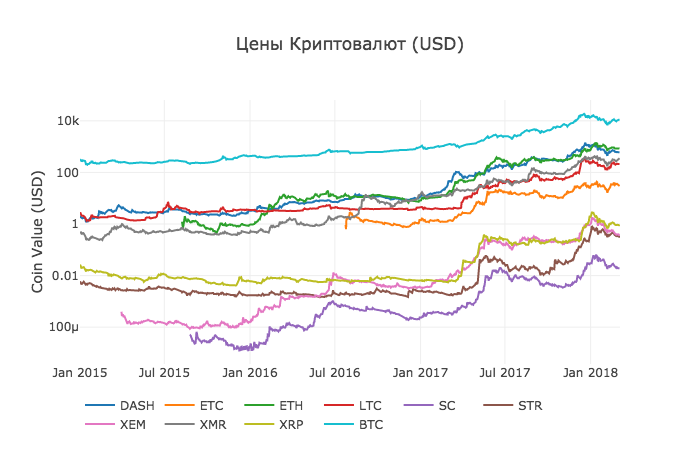
In this example, we use the logarithmic scale of the Y axis to compare all currencies in the same area. You can try different parameter values ​​(for example, scale = 'linear') to get different points of view on the data.

Step 3.4 - Calculation of cryptocurrency correlation.

You may notice that cryptocurrency exchange rates, despite their completely different values ​​and volatility, seem slightly correlated. And as seen from the surge in April 2017, even small fluctuations seem to occur synchronously in the entire market.

We can test our correlation hypothesis using the Pandas corr () method, which calculates the Pearson correlation coefficient for each column in a data set relative to each other. In the calculation, we also use the pct_change () method, which converts each cell in the dataset from the absolute value of the price to the percentage change.

First, we calculate the correlations for 2016.

 combined_df_2016 = combined_df[combined_df.index.year == 2016] combined_df_2016.pct_change().corr(method='pearson') 

Result:

	DASH	Etc	Eth	LTC	SC	STR	XEM	Xmr	Xrp	Btc
DASH	1.000000	0.003992	0.122695	-0.012194	0.026602	0.058083	0.014571	0.121537	0.088657	-0.014040
Etc	0.003992	1.000000	-0.181991	-0.131079	-0.008066	-0.102654	-0.080938	-0.105898	-0.054095	-0.170538
Eth	0.122695	-0.181991	1.000000	-0.064652	0.169642	0.035093	0.043205	0.087216	0.085630	-0.006502
LTC	-0.012194	-0.131079	-0.064652	1.000000	0.012253	0.113523	0.160667	0.129475	0.053712	0.750174
SC	0.026602	-0.008066	0.169642	0.012253	1.000000	0.143252	0.106153	0.047910	0.021098	0.035116
STR	0.058083	-0.102654	0.035093	0.113523	0.143252	1.000000	0.225132	0.027998	0.320116	0.079075
XEM	0.014571	-0.080938	0.043205	0.160667	0.106153	0.225132	1.000000	0.016438	0.101326	0.227674
Xmr	0.121537	-0.105898	0.087216	0.129475	0.047910	0.027998	0.016438	1.000000	0.027649	0.127520
Xrp	0.088657	-0.054095	0.085630	0.053712	0.021098	0.320116	0.101326	0.027649	1.000000	0.044161
Btc	-0.014040	-0.170538	-0.006502	0.750174	0.035116	0.079075	0.227674	0.127520	0.044161	1.000000

Coefficients close to 1 or -1 mean that the data correlate strongly or inversely correlate, respectively, and coefficients close to zero mean that the values ​​tend to fluctuate independently of each other.

To visualize these results, we will create another helper function.

 def correlation_heatmap(df, title, absolute_bounds=True): heatmap = go.Heatmap( z=df.corr(method='pearson').as_matrix(), x=df.columns, y=df.columns, colorbar=dict(title='Pearson Coefficient'), ) layout = go.Layout(title=title) if absolute_bounds: heatmap['zmax'] = 1.0 heatmap['zmin'] = -1.0 fig = go.Figure(data=[heatmap], layout=layout) py.iplot(fig) 

 correlation_heatmap(combined_df_2016.pct_change(), "  (2016)") 

Here, the dark red values ​​represent strong correlations, and the blue values ​​represent strong inverse correlations. All other colors represent different degrees of weak / non-existent correlations.

What does this chart tell us? In fact, this shows that there was very little statistically significant connection between how prices of different cryptocurrencies fluctuated during 2016.

Now, to test our hypothesis that cryptotermines have become more correlated in recent months, we repeat the same tests using data for 2017 and 2018.

 combined_df_2017 = combined_df[combined_df.index.year == 2017] combined_df_2017.pct_change().corr(method='pearson') 

Result:

	DASH	Etc	Eth	LTC	SC	STR	XEM	Xmr	Xrp	Btc
DASH	1.000000	0.387555	0.506911	0.340153	0.291424	0.183038	0.325968	0.498418	0.091146	0.307095
Etc	0.387555	1.000000	0.601437	0.482062	0.298406	0.210387	0.321852	0.447398	0.114780	0.416562
Eth	0.506911	0.601437	1.000000	0.437609	0.373078	0.259399	0.399200	0.554632	0.212350	0.410771
LTC	0.340153	0.482062	0.437609	1.000000	0.339144	0.307589	0.379088	0.437204	0.323905	0.420645
SC	0.291424	0.298406	0.373078	0.339144	1.000000	0.402966	0.331350	0.378644	0.243872	0.325318
STR	0.183038	0.210387	0.259399	0.307589	0.402966	1.000000	0.339502	0.327488	0.509828	0.230957
XEM	0.325968	0.321852	0.399200	0.379088	0.331350	0.339502	1.000000	0.336076	0.268168	0.329431
Xmr	0.498418	0.447398	0.554632	0.437204	0.378644	0.327488	0.336076	1.000000	0.226636	0.409183
Xrp	0.091146	0.114780	0.212350	0.323905	0.243872	0.509828	0.268168	0.226636	1.000000	0.131469
Btc	0.307095	0.416562	0.410771	0.420645	0.325318	0.230957	0.329431	0.409183	0.131469	1.000000

 correlation_heatmap(combined_df_2017.pct_change(), "  (2017)") 

 combined_df_2018 = combined_df[combined_df.index.year == 2018] combined_df_2018.pct_change().corr(method='pearson') 

	DASH	Etc	Eth	LTC	SC	STR	XEM	Xmr	Xrp	Btc
DASH	1.000000	0.775561	0.856549	0.847947	0.733168	0.717240	0.769135	0.913044	0.779651	0.901523
Etc	0.775561	1.000000	0.808820	0.667434	0.530840	0.551207	0.641747	0.696060	0.637674	0.694228
Eth	0.856549	0.808820	1.000000	0.700708	0.624853	0.630380	0.752303	0.816879	0.652138	0.787141
LTC	0.847947	0.667434	0.700708	1.000000	0.683706	0.596614	0.593616	0.765904	0.644155	0.831780
SC	0.733168	0.530840	0.624853	0.683706	1.000000	0.615265	0.695136	0.626091	0.719462	0.723976
STR	0.717240	0.551207	0.630380	0.596614	0.615265	1.000000	0.790420	0.642810	0.854057	0.669746
XEM	0.769135	0.641747	0.752303	0.593616	0.695136	0.790420	1.000000	0.744325	0.829737	0.734044
Xmr	0.913044	0.696060	0.816879	0.765904	0.626091	0.642810	0.744325	1.000000	0.668016	0.888284
Xrp	0.779651	0.637674	0.652138	0.644155	0.719462	0.854057	0.829737	0.668016	1.000000	0.712146
Btc	0.901523	0.694228	0.787141	0.831780	0.723976	0.669746	0.734044	0.888284	0.712146	1.000000

 correlation_heatmap(combined_df_2018.pct_change(), "  (2018)")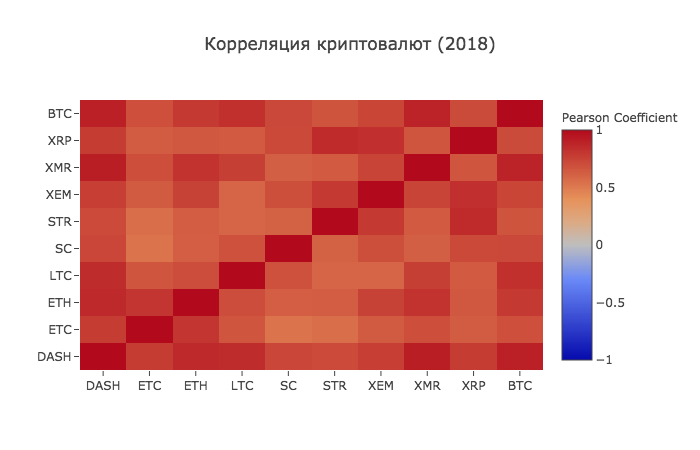 

And here we see what we assumed - almost all cryptocurrencies have become more interconnected with each other in all directions.

At this point, we assume that the introduction to working with data in Anaconda has been successfully passed.