Gini coefficient. From economics to machine learning
The Gini Coefficient (Gini Coefficient) is a quality metric that is often used when evaluating predictive models in problems of binary classification in conditions of a strong imbalance of classes of the target variable. That it is widely used in the tasks of bank lending, insurance and targeted marketing. To fully understand this metric, we first need to plunge into the economy and figure out what it is used for.
Economy
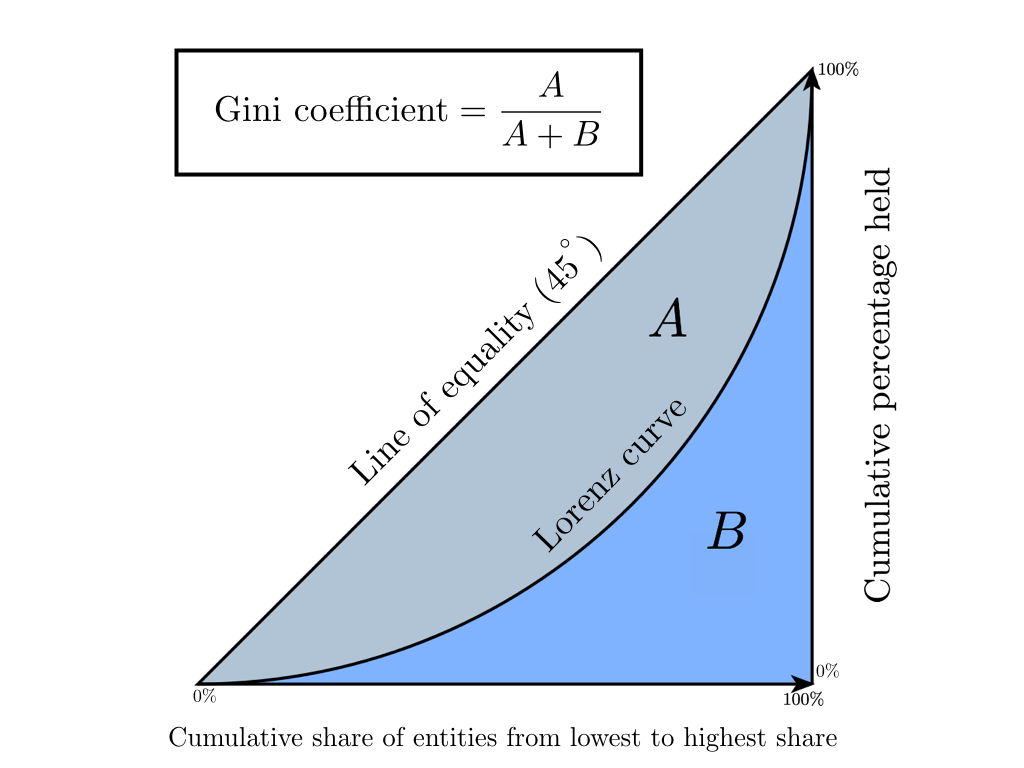
The Gini coefficient is a statistical indicator of the degree of social stratification with respect to any economic attribute (annual income, property, real estate) used in countries with developed market economies. Basically, the level of annual income is taken as a calculated indicator. The coefficient shows the deviation of the actual distribution of income in society from their absolutely equal distribution among the population and allows one to very accurately assess the uneven distribution of income in society. It is worth noting that a little earlier the birth of the Gini coefficient, in 1905, the American economist Max Lorenz, in his work Methods of Measuring the Concentration of Wealth, proposed a method of measuring the concentration of the welfare of society, later called the Lorenz Curve. Further, we will show that the Gini Coefficient is an absolutely accurate algebraic interpretation of the Lorentz curve, and it in turn is its graphic display.
')
Lorenz curve is a graphical representation of the share of total income per each population group. The diagonal on the graph corresponds to the “line of absolute equality” - the income of the entire population is the same.
The Gini coefficient varies from 0 to 1. The more its value deviates from zero and approaches one, the more concentrated the incomes are in the hands of certain groups of the population and the higher the level of social inequality in the state, and vice versa. Sometimes a percentage representation of this factor is used, called the Gini index (value ranges from 0% to 100%).
In economics, there are several ways to calculate this coefficient, we will focus on the Brown formula (it is first necessary to create a variation series - to rank the population by income):
G = 1 - s u m n k = 1 ( X k - X k - 1 ) ( Y k + Y k - 1 )
Where n - number of inhabitants X k - cumulative share of the population, Y k - cumulative share of income for X k
Let's analyze the above on a toy example in order to intuitively understand the meaning of this statistic.
Suppose there are three villages, each of which has 10 inhabitants. In each village, the total annual income of the population is 100 rubles. In the first village, all residents earn the same amount - 10 rubles a year, in the second village, income distribution is different: 3 people earn 5 rubles each, 4 people 10 rubles each and 3 people 15 rubles each. And in the third village 7 people get 1 ruble per year, 1 person - 10 rubles, 1 person - 33 rubles and one person - 50 rubles. For each village, we calculate the Gini coefficient and construct the Lorenz curve.
We present the initial data for the villages in the form of a table and immediately calculate X k and Y k for clarity:
import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline import warnings warnings.filterwarnings('ignore') village = pd.DataFrame({'Person':['Person_{}'.format(i) for i in range(1,11)], 'Income_Village_1':[10]*10, 'Income_Village_2':[5,5,5,10,10,10,10,15,15,15], 'Income_Village_3':[1,1,1,1,1,1,1,10,33,50]}) village['Cum_population'] = np.cumsum(np.ones(10)/10) village['Cum_Income_Village_1'] = np.cumsum(village['Income_Village_1']/100) village['Cum_Income_Village_2'] = np.cumsum(village['Income_Village_2']/100) village['Cum_Income_Village_3'] = np.cumsum(village['Income_Village_3']/100) village = village.iloc[:, [3,4,0,5,1,6,2,7]] village 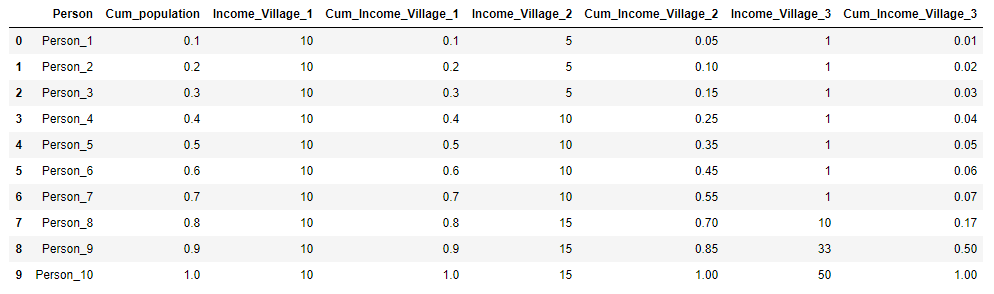
plt.figure(figsize = (8,8)) Gini=[] for i in range(1,4): X_k = village['Cum_population'].values X_k_1 = village['Cum_population'].shift().fillna(0).values Y_k = village['Cum_Income_Village_{}'.format(i)].values Y_k_1 = village['Cum_Income_Village_{}'.format(i)].shift().fillna(0).values Gini.append(1 - np.sum((X_k - X_k_1) * (Y_k + Y_k_1))) plt.plot(np.insert(X_k,0,0), np.insert(village['Cum_Income_Village_{}'.format(i)].values,0,0), label=' {} (Gini = {:0.2f})'.format(i, Gini[i-1])) plt.title(' ') plt.xlabel(' ') plt.ylabel(' ') plt.legend(loc="upper left") plt.xlim(0, 1) plt.ylim(0, 1) plt.show() 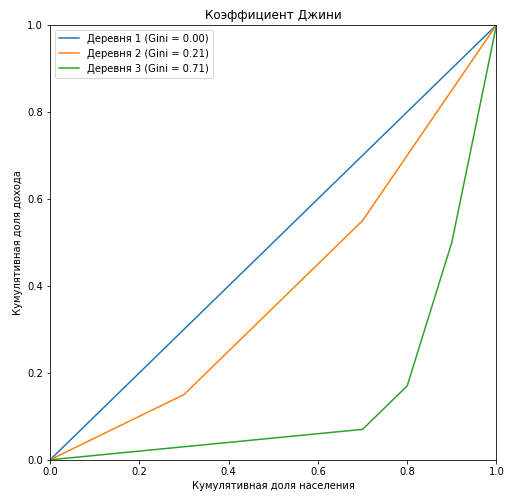
It can be seen that the Lorentz curve for the Gini coefficient in the first village completely coincides with the diagonal (“line of absolute equality”), and the greater the stratification among the population relative to the annual income, the greater the area of the figure formed by the Lorentz curve and diagonal. Let us show by the example of the third village that the ratio of the area of this figure to the area of the triangle formed by the line of absolute equality is exactly equal to the value of the Gini coefficient:
curve_area = np.trapz(np.insert(village['Cum_Income_Village_3'].values,0,0), np.insert(village['Cum_population'].values,0,0)) S = (0.5 - curve_area) / 0.5 plt.figure(figsize = (8,8)) plt.plot([0,1],[0,1],linestyle = '--',lw = 2,color = 'black') plt.plot(np.insert(village['Cum_population'].values,0,0), np.insert(village['Cum_Income_Village_3'].values,0,0), label=' {} (Gini = {:0.2f})'.format(i, Gini[i-1]),lw = 2,color = 'green') plt.fill_between(np.insert(X_k,0,0), np.insert(X_k,0,0), y2=np.insert(village['Cum_Income_Village_3'].values,0,0), alpha=0.5) plt.text(0.45,0.27,'S = {:0.2f}'.format(S),fontsize = 28) plt.title(' ') plt.xlabel(' ') plt.ylabel(' ') plt.legend(loc="upper left") plt.xlim(0, 1) plt.ylim(0, 1) plt.show() 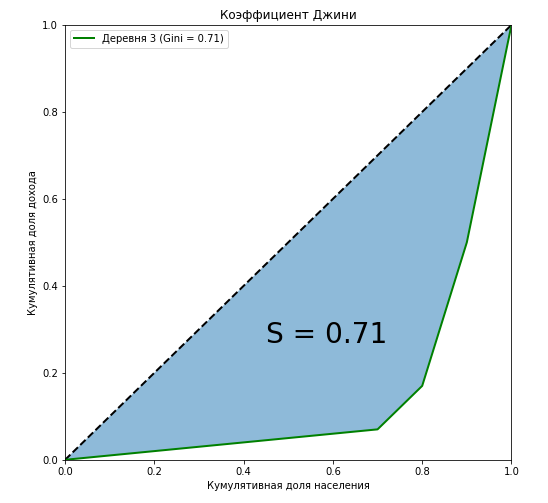
We showed that, along with algebraic methods, one of the ways to calculate the Gini coefficient is geometric - calculating the area share between the Lorenz curve and the line of absolute equality of incomes from the total area under the straight line of absolute equality of incomes.
Another important point. Let's mentally fix the ends of the curve in points ( 0 , 0 ) and ( 1 , 1 ) and begin to change its shape. It is quite obvious that the area of the figure will not change, but in so doing we transfer members of society from the “middle class” to the poor or the rich without changing the income ratio between the classes. Take for example ten people with the following income:
[ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 20 , 72 ]
Now Sharikov’s “Select and Divide!” Method is applied to a person with an income of “20”, redistributing his income proportionally among the rest of the society. In this case, the Gini coefficient will not change and will remain at 0.772, we simply pulled the “fixed” Lorenz curve to the x-axis and changed its shape:
[1+11.1/20,1+11.1/20,1+11.1/20,1+11.1/20,1+11.1/20,1+11.1/20,1+11.1/20,1+11.1/20,1+11.1/20,72+8.9/20]
Let's look at another important point: calculating the Gini coefficient, we do not classify people into poor and rich, it does not depend on whom we consider to be poor or oligarch. But suppose that we faced such a task, for this, depending on what we want to get, what our goals are, we will need to set the income threshold to clearly divide people into poor and rich. If you saw in this the analogy with the Threshold of the problems of binary classification, then it is time for us to move to machine learning.
Machine learning
1. General understanding
Immediately it is worth noting that, having come to machine learning, the Gini coefficient has changed a lot: it is calculated differently and has a different meaning. Numerically, the coefficient is equal to the area of the figure formed by the line of absolute equality and the Lorenz curve. There are also similarities with a relative from the economy, for example, we still need to build the Lorenz curve and calculate the area of the figures. And most importantly, the curve construction algorithm has not changed. The Lorenz curve has also undergone changes, it has received the name Lift Curve and is a mirror image of the Lorenz curve with respect to the line of absolute equality (due to the fact that the ranking of probabilities does not occur in ascending but descending). Let's sort it all out on the next toy example. To minimize the error in calculating the areas of the figures, we will use the functions scipy interp1d (interpolation of a one-dimensional function) and quad (calculation of a definite integral).
Suppose we solve the problem of binary classification for 15 objects and we have the following distribution of classes:
[1,1,1,1,1,1,0,0,0,0,0,0,0,0,0]
Our trained algorithm predicts the following attitudes towards the class “1” on these objects:

We calculate the Gini coefficient for two models: our trained algorithm and an ideal model that accurately predicts classes with a probability of 100%. The idea is as follows: instead of ranking the population by income level, we rank the predicted probabilities of the model in descending order and substitute into the formula the cumulative fraction of the true values of the target variable corresponding to the predicted probabilities. In other words, we sort the table by the line “Predict” and consider the cumulative share of classes instead of the cumulative share of income.

from scipy.interpolate import interp1d from scipy.integrate import quad actual = [1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0] predict = [0.9, 0.3, 0.8, 0.75, 0.65, 0.6, 0.78, 0.7, 0.05, 0.4, 0.4, 0.05, 0.5, 0.1, 0.1] data = zip(actual, predict) sorted_data = sorted(data, key=lambda d: d[1], reverse=True) sorted_actual = [d[0] for d in sorted_data] cumulative_actual = np.cumsum(sorted_actual) / sum(actual) cumulative_index = np.arange(1, len(cumulative_actual)+1) / len(predict) cumulative_actual_perfect = np.cumsum(sorted(actual, reverse=True)) / sum(actual) x_values = [0] + list(cumulative_index) y_values = [0] + list(cumulative_actual) y_values_perfect = [0] + list(cumulative_actual_perfect) f1, f2 = interp1d(x_values, y_values), interp1d(x_values, y_values_perfect) S_pred = quad(f1, 0, 1, points=x_values)[0] - 0.5 S_actual = quad(f2, 0, 1, points=x_values)[0] - 0.5 fig, ax = plt.subplots(nrows=1,ncols=2, sharey=True, figsize=(14, 7)) ax[0].plot(x_values, y_values, lw = 2, color = 'blue', marker='x') ax[0].fill_between(x_values, x_values, y_values, color = 'blue', alpha=0.1) ax[0].text(0.4,0.2,'S = {:0.4f}'.format(S_pred),fontsize = 28) ax[1].plot(x_values, y_values_perfect, lw = 2, color = 'green', marker='x') ax[1].fill_between(x_values, x_values, y_values_perfect, color = 'green', alpha=0.1) ax[1].text(0.4,0.2,'S = {:0.4f}'.format(S_actual),fontsize = 28) for i in range(2): ax[i].plot([0,1],[0,1],linestyle = '--',lw = 2,color = 'black') ax[i].set(title=' ', xlabel=' ', ylabel=' ', xlim=(0, 1), ylim=(0, 1)) plt.show(); 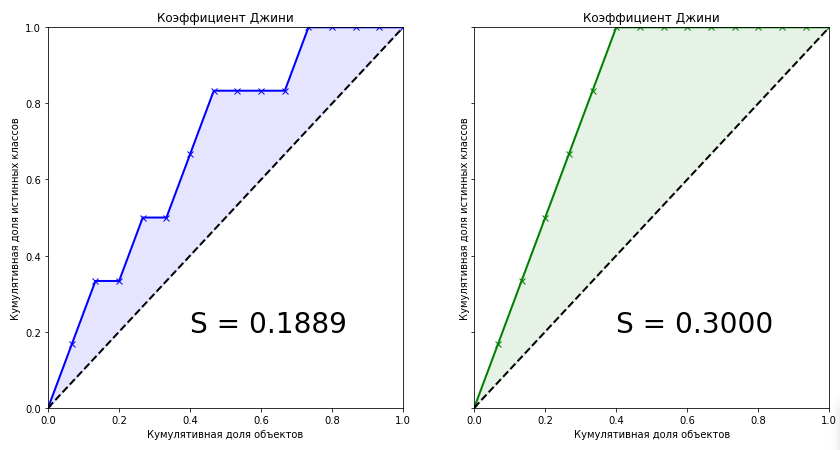
The Gini coefficient for a trained model is 0.1889. Is it a little or a lot? How accurate is the algorithm? Without knowing the exact value of the coefficient for an ideal algorithm, we cannot say anything about our model. Therefore, the metric of quality in machine learning is the normalized Gini coefficient , which is equal to the ratio of the coefficient of the trained model to the coefficient of the ideal model. Further, under the term "Gini Coefficient" we will mean just that.
Gininormalized= fracGinimodelGiniperfect(1)
Looking at these two graphs, we can draw the following conclusions:
- The prediction of the ideal algorithm is the maximum Gini coefficient for the current data set and depends only on the true distribution of classes in the problem.
- The area of the shape for an ideal algorithm is:
S= fracNumber enspaceofobjects enspaceofclass enspace0 enspacein enspacesection2
- The predictions of the trained models can not be greater than the value of the coefficient of an ideal algorithm.
- With a uniform distribution of classes of the target variable, the Gini coefficient of an ideal algorithm will always be equal to 0.25
- For an ideal algorithm, the shape of the shape formed by the Lift Curve and the line of absolute equality will always be a triangle.
- The Gini coefficient of the random algorithm is 0, and the Lift Curve coincides with the line of absolute equality.
- The Gini coefficient of a trained algorithm will always be less than the coefficient of an ideal algorithm.
- The values of the normalized Gini coefficient for the trained algorithm are in the interval [0,1] .
- The normalized Gini coefficient is a metric of quality that needs to be maximized.
2. Algebraic representation. Proof of linear connection with AUC ROC
We come to the most interesting point - the algebraic representation of the Gini coefficient. How to calculate this metric? She is not equal to her relative from the economy. It is known that the coefficient can be calculated by the following formula:
Gininormalized=2∗AUCROC−1 hspace15pt(2)
I honestly tried to find the conclusion of this formula on the Internet, but did not find anything. Even in foreign books and scientific articles. But on some questionable sites of statistics lovers there was a phrase: “It is so obvious that there is nothing to discuss. It’s enough to compare the Lift Curve and ROC Curve charts so that everything becomes clear at once . ” A little later, when I myself derived the connection formula for these two metrics, I realized that this phrase was an excellent indicator. If you hear or read it, it is obvious only that the author of the phrase has no understanding of the Gini coefficient. Let's take a look at the Lift Curve and ROC Curve charts for our example:
from sklearn.metrics import roc_curve, roc_auc_score aucroc = roc_auc_score(actual, predict) gini = 2*roc_auc_score(actual, predict)-1 fpr, tpr, t = roc_curve(actual, predict) fig, ax = plt.subplots(nrows=1,ncols=3, sharey=True, figsize=(15, 5)) fig.suptitle('Gini = 2 * AUCROC - 1 = {:0.2f}\n\n'.format(gini),fontsize = 18, fontweight='bold') ax[0].plot([0]+fpr.tolist(), [0]+tpr.tolist(), lw = 2, color = 'red') ax[0].fill_between([0]+fpr.tolist(), [0]+tpr.tolist(), color = 'red', alpha=0.1) ax[0].text(0.4,0.2,'S = {:0.2f}'.format(aucroc),fontsize = 28) ax[1].plot(x_values, y_values, lw = 2, color = 'blue') ax[1].fill_between(x_values, x_values, y_values, color = 'blue', alpha=0.1) ax[1].text(0.4,0.2,'S = {:0.2f}'.format(S_pred),fontsize = 28) ax[2].plot(x_values, y_values_perfect, lw = 2, color = 'green') ax[2].fill_between(x_values, x_values, y_values_perfect, color = 'green', alpha=0.1) ax[2].text(0.4,0.2,'S = {:0.2f}'.format(S_actual),fontsize = 28) ax[0].set(title='ROC-AUC', xlabel='False Positive Rate', ylabel='True Positive Rate', xlim=(0, 1), ylim=(0, 1)) for i in range(1,3): ax[i].plot([0,1],[0,1],linestyle = '--',lw = 2,color = 'black') ax[i].set(title=' ', xlabel=' ', ylabel=' ', xlim=(0, 1), ylim=(0, 1)) plt.show(); 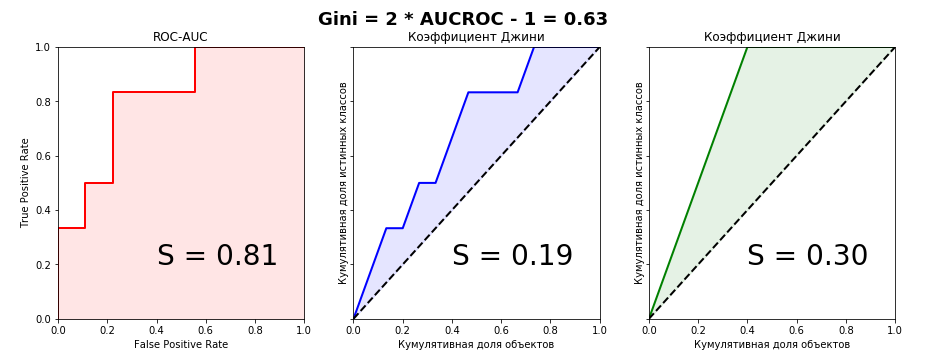
It is clearly seen that it is impossible to catch a connection from the graphical representation of metrics, therefore we will prove equality algebraically. I managed to do it in two ways - parametrically (by integrals) and non-parametrically (through Wilcoxon-Mann-Whitney statistics). The second method is much simpler and without multi-storey fractions with double integrals, so we’ll dwell on it in detail. For further consideration of the evidence, we define the terminology: the cumulative share of true classes is none other than the True Positive Rate. The cumulative share of objects is in turn the number of objects in the ranked row (when scaling by interval (0,1) - respectively, the proportion of objects).
Understanding the proof requires a basic understanding of the ROC-AUC metric - what it is all about, how the graph is constructed and in which axes. I recommend an article from Alexander Dyakonov ’s blog “AUC ROC (area under the error curve)”
We introduce the following notation:
- n - The number of objects in the sample
- n0 - The number of objects of class "0"
- n1 - The number of objects of class "1"
- Tp - True Positive (the correct answer of the model on the true class "1" at a given threshold)
- FP - False Positive (incorrect response of the model on the true class "0" at a given threshold)
- TPR - True Positive Rate (ratio Tp to n1 )
- FPR - False Positive Rate (ratio FP to n0 )
- i,j - the current index of the item.
Parametric method
The parametric equation for ROC curve can be written as follows:
AUC= int10TPR enspacedFPR= int10 fracTPn1 enspaced fracFPn0= frac1n1∗n0 int10TP enspacedFP hspace35pt(3)
When plotting the Lift Curve plot X we postponed the proportion of objects (their number) previously sorted in descending order. Thus, the parametric equation for the Gini coefficient will be as follows:
AUC= int10TPR enspaced fracTP+FPn1+n0−0.5 hspace35pt(4)
Substituting expression (4) into expression (1) for both models and transforming it, we will see that expression (3) can be substituted into one of the parts, which ultimately gives us a beautiful formula of a normalized Gini (2)
Nonparametric method
In the proof, I relied on the elementary postulates of the Theory of Probability. It is known that the numerical value of the AUC ROC is equal to the statistics of Wilcoxon-Mann-Whitney:
AUCROC= frac sumn1i=1 sumn0j=1S(xi,xj)n1∗n0 hspace15pt(5)
S(xi,xj)= begincases1, enspacexi>xj frac12, enspacexi=xj0, enspacexi<xj endcases
Where xi - the answer of the algorithm on the i-th object from the distribution "1", xj - the response of the algorithm on the j-th object from the distribution of "0"
The proof of this formula can, for example, be found here.
This is interpreted very intuitively: if you randomly extract a pair of objects, where the first object will be from the distribution "1" and the second from the distribution "0", then the probability that the first object will have a predicted value greater or equal than the predicted value of the second object, equal to the value of the AUC ROC. Combinatorial it is easy to calculate that the number of pairs of such objects will be: n1∗n0 .
Let the model predict k possible values from the set S = \ {s_1, \ dots, s_k \} where s1< enspace... enspace<sk and S - some probability distribution, the elements of which take values on the interval [0,1] .
Let be Sn1 set of values that objects take n1 and Sn1 subseteqS . Let be Sn0 set of values that objects take n0 and Sn0 subseteqS . Obviously, the sets Sn1 and Sn0 may intersect.
Denote pin0 like the probability that the object n0 will take value si and pin1 like the probability that the object n1 will take value si . Then sumki=1pin0=1 and sumki=1pin1=1
Having a prior probability pi for each sample object, we can write a formula that determines the probability that the object will take the value si :
pin= pipin0+(1− pi)pin1
We define three distribution functions:
- for objects of class "1"
- for objects of class "0"
- for all sample objects
CDFin1= sumij=1pin1 hspace10pti=1, dots,k
CDFin0= sumij=1pin0 hspace10pti=1, dots,k
CDFin= sumij=1pin hspace10pti=1, dots,k
An example of how the distribution functions for two classes may look like in a credit scoring task:
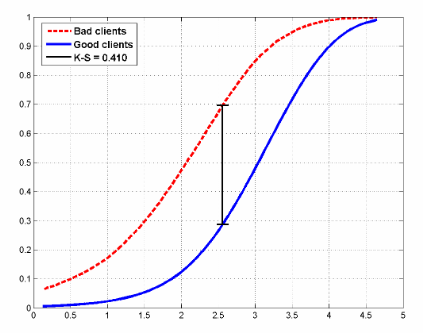
The figure also shows the statistics of Kolmogorov-Smirnov, which is also used to evaluate models.
We write the Wilcoxon formula in a probabilistic form and transform it:
AUCROC=P(Sn1>Sn1)+ frac12P(Sn1=Sn1)= sumki=1P(Sn1 geqsi−1)P(Sn0=si)+ frac12 sumki=1P(Sn1=si)P(Sn0=si)= sumki=1 big((P(Sn1 geqsi−1)+ frac12P(Sn1=si) big)P(Sn0=si)= sumki=1 frac12 big((P(Sn1 geqsi)+(P(Sn1 geqsi−1) big)P(Sn0=si)= sumki=1 frac12(CDFin1+CDFi−1n1)(CDFin0−CDFi−1n0) hspace15pt(6)
We can write a similar formula for the area under the Lift Curve (remember that it consists of the sum of two areas, one of which is always 0.5):
AUCLift=Ginimodel+0.5= sumki=1 frac12(CDFin1+CDFi−1n1)(CDFin−CDFi−1n) hspace15pt(7)
And now we will transform it:
AUCLift=Gini+0.5= sumki=1 frac12(CDFin1+CDFi−1n1)(CDFin−CDFi−1n)= sumki=1 frac12(CDFin1+CDFi−1n1) big( pi(CDFin1−CDFi−1n1)+(1− pi)(CDFin0−CDFi−1n0) big)=(1− pi) sumki=1 frac12(CDFin1+CDFi−1n1)(CDFin0−CDFi−1n0)++ pi sumki=1 frac12(CDFin1+CDFi−1n1)(CDFin1−CDFi−1n1)=(1− pi)AUCROC+ frac12 pi sumki=1 big((CDFin1)2−(CDFi−1n0)2 big)=(1− pi)AUCROC+ frac12 pi hspace15pt(8)
For an ideal model, the formula is written simply:
Giniperfect= frac12(1− pi) hspace15pt(9)
Hence from (8) and (9), we get:
Gininormalized= fracGinimodelGiniperfect= frac(1− pi)AUCROC+ frac1 2 f r a c 1 2 ( 1 - p i ) =2AUCROC-1
As they said in school, that was required to prove.
3. Practical application
As mentioned at the beginning of the article, the Gini coefficient is used to evaluate models in many areas, including in banking lending, insurance and targeted marketing. And this is quite a reasonable explanation. This article does not aim to elaborate on the practical application of statistics in a particular area. Many books have been written on this topic, we will only briefly go over this topic.
Credit scoring
Worldwide, banks receive thousands of loan applications every day. Of course, it is necessary to somehow assess the risks that the client may simply not repay the loan, therefore, predictive models are developed that assess the probability that the client does not pay the loan, and these models first need to be somehow assessed and If the model is successful, then choose the optimal threshold (threshold) of probability. The choice of the optimal threshold is determined by the policy of the bank. The task of analysis in the selection of the threshold is to minimize the risk of loss of profits associated with the refusal to issue a loan. But in order to choose a threshold, one must have a qualitative model. The main metrics of quality in the banking sector:
- Gini coefficient
- Kolmogorov-Smirnov statistics (calculated as the maximum difference between the cumulative distribution functions of "bad" and "good" borrowers. Above in the article, a picture with distributions and these statistics was cited)
- The divergence coefficient (is an estimate of the difference in mathematical expectations of scoring points distributions for “bad” and “good” borrowers, normalized by the variances of these distributions. The greater the value of the divergence coefficient, the better the quality of the model.)
I don’t know how things are in Russia, although I live here, but in Europe the Gini coefficient is the most widely used, in North America - the Kolmogorov-Smirnov statistics.
Insurance
In this area, everything is similar to the banking sector, with the only difference being that we need to divide customers into those who submit insurance claims and those who do not. Consider a practical example from this area, in which one feature of the Lift Curve will be clearly visible - with highly unbalanced classes in the target variable, the curve almost perfectly coincides with the ROC curve.
A few months ago, Kaggle hosted the Porto Seguro's Safe Driver Prediction competition, in which the task was just predicting Insurance Claim - filing an insurance claim. And in which I, on my own stupidity, missed silver, choosing the wrong submission.

It was a very strange and at the same time incredibly informative competition. And with a record number of participants - 5169. The winner of the competition, Michael Jahrer, wrote code only in C ++ / CUDA, and this causes admiration and respect.
Porto Seguro is a Brazilian auto insurance company.
Dataset consisted of 595207 lines in the train, 892816 lines in the test and 53 anonymized characters. The ratio of classes in the target is 3% and 97%.Let's write a simple baseline, since this is done in a couple of lines, and we will build graphs. Please note that the curves almost perfectly match, the difference in the areas under the Lift Curve and the ROC Curve is 0.005.
from sklearn.model_selection import train_test_split import xgboost as xgb from scipy.interpolate import interp1d from scipy.integrate import quad df = pd.read_csv('train.csv', index_col='id') unwanted = df.columns[df.columns.str.startswith('ps_calc_')] df.drop(unwanted,inplace=True,axis=1) df.fillna(-999, inplace=True) train, test = train_test_split(df, stratify=df.target, test_size=0.25, random_state=1) estimator = xgb.XGBClassifier(seed=1, n_jobs=-1) estimator.fit(train.drop('target', axis=1), train.target) pred = estimator.predict_proba(test.drop('target', axis=1))[:, 1] test['predict'] = pred actual = test.target.values predict = test.predict.values data = zip(actual, predict) sorted_data = sorted(data, key=lambda d: d[1], reverse=True) sorted_actual = [d[0] for d in sorted_data] cumulative_actual = np.cumsum(sorted_actual) / sum(actual) cumulative_index = np.arange(1, len(cumulative_actual)+1) / len(predict) cumulative_actual_perfect = np.cumsum(sorted(actual, reverse=True)) / sum(actual) aucroc = roc_auc_score(actual, predict) gini = 2*roc_auc_score(actual, predict)-1 fpr, tpr, t = roc_curve(actual, predict) x_values = [0] + list(cumulative_index) y_values = [0] + list(cumulative_actual) y_values_perfect = [0] + list(cumulative_actual_perfect) fig, ax = plt.subplots(nrows=1,ncols=3, sharey=True, figsize=(18, 6)) fig.suptitle('Gini = {:0.3f}\n\n'.format(gini),fontsize = 26, fontweight='bold') ax[0].plot([0]+fpr.tolist(), [0]+tpr.tolist(), lw=2, color = 'red') ax[0].plot([0]+fpr.tolist(), [0]+tpr.tolist(), lw = 2, color = 'red') ax[0].fill_between([0]+fpr.tolist(), [0]+tpr.tolist(), color = 'red', alpha=0.1) ax[0].text(0.4,0.2,'S = {:0.3f}'.format(aucroc),fontsize = 28) ax[1].plot(x_values, y_values, lw = 2, color = 'blue') ax[1].fill_between(x_values, x_values, y_values, color = 'blue', alpha=0.1) ax[1].text(0.4,0.2,'S = {:0.3f}'.format(S_pred),fontsize = 28) ax[2].plot(x_values, y_values_perfect, lw = 2, color = 'green') ax[2].fill_between(x_values, x_values, y_values_perfect, color = 'green', alpha=0.1) ax[2].text(0.4,0.2,'S = {:0.3f}'.format(S_actual),fontsize = 28) ax[0].set(title='ROC-AUC XGBoost Baseline', xlabel='False Positive Rate', ylabel='True Positive Rate', xlim=(0, 1), ylim=(0, 1)) ax[1].set(title='Gini XGBoost Baseline') ax[2].set(title='Gini Perfect') for i in range(1,3): ax[i].plot([0,1],[0,1],linestyle = '--',lw = 2,color = 'black') ax[i].set(xlabel='Share of clients', ylabel='True Positive Rate', xlim=(0, 1), ylim=(0, 1)) plt.show(); 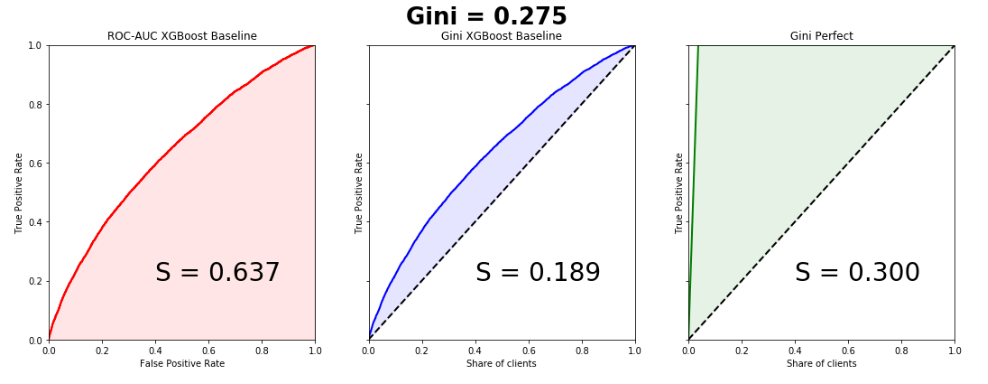
The Gini coefficient of the winning model is 0.29698.
For me, there is still a mystery about what the organizers wanted to achieve by zonimizing the signs and making an incredible data preprocessing. This is one of the reasons why all models, including the winners, in fact turned out to be garbage. Probably just PR, before no one in the world knew about Porto Seguro except Brazilians, now many people know.
Targeted marketing
In this area, you can best understand the true meaning of the Gini and Lift Curve coefficient. For some reason, almost all books and articles provide examples of email marketing campaigns, which in my opinion is an anachronism. Create an artificial business problem from the scope of free2play games . We have a database of users who once played our game and for some reason fell off. We want to return them to our game project, for each user we have a certain indicative space (time in the project, how much he spent, what level he reached, etc.) on the basis of which we build the model. Evaluate the model by the Gini coefficient and build the Lift Curve:

Suppose that as part of a marketing campaign, we in one way or another make contact with the user (email, social networks), the price of contact with one user is 2 rubles. We know that Lifetime Value is 5 rubles. It is necessary to optimize the effectiveness of the marketing campaign. Suppose there are a total of 100 users in the sample, of which 30 will return. Thus, if we establish contact with 100% of users, then we will spend 200 rubles on a marketing campaign and will receive an income of 150 rubles. This is a campaign failure. Consider the Lift Curve chart. It is seen that in contact with 50% of users, we are in contact with 90% of users who return. campaign costs - 100 rubles, income 135. We are in the black. Thus, Lift Curve allows us to optimize our marketing company in the best possible way.
4. Bubble Sort
The Gini coefficient has a rather amusing but very useful interpretation, with the help of which we can also easily calculate it. It turns out that it is numerically equal to:
G i n i n o r m a a l i z e d = S w a p s r a n d o m - S w a p s s o r t e dS w a p s r a n d o m
Where, S w a p s s o r t e d the number of permutations that must be made in the ranked list in order to obtain a true list of the target variableS w a p s r a n d o m is the number of permutations for the predictions of the random algorithm. We write an elementary bubble sort and show it:
[1,1,1,1,1,1,0,0,0,0,0,0,0,0,0][1,1,0,1,0,1,1,0,0,0,1,0,0,0,0]
actual = [1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0] predict = [0.9, 0.3, 0.8, 0.75, 0.65, 0.6, 0.78, 0.7, 0.05, 0.4, 0.4, 0.05, 0.5, 0.1, 0.1] data = zip(actual, predict) sorted_data = sorted(data, key=lambda d: d[1], reverse=False) sorted_actual = [d[0] for d in sorted_data] swaps=0 n = len(sorted_actual) array = sorted_actual for i in range(1,n): flag = 0 for j in range(ni): if array[j]>array[j+1]: array[j], array[j+1] = array[j+1], array[j] flag = 1 swaps+=1 if flag == 0: break print(" : ", swaps) : 10It is easy to combinatorially count the number of permutations for a random algorithm:
S w a p s r a n d o m = 6 ∗ 92 =27
In this way:
G i n i n o r m a l i z e d = 27 - 1027 =0.63
We see that we have obtained the value of the coefficient, as in the toy example considered above.
I hope the article was helpful and dispelled some myths about this quality metric.
Source: https://habr.com/ru/post/350440/
All Articles