Play with ormats
I suggest you play a game. I give you a square grid on which some cells are painted over and some may remain empty. We will call it a "template." For example, a grid could be one of these patterns:

Do you have a stack of transparent plastic sheets, in size and shape that coincide with the grid, on which the patterns of black dots are applied:

It is worth noting that in each of these patterns exactly three points, one point in each row and column. The six combinations shown are the only 3 × 3 grids with this property.
')
Your task is to assemble a subset of transparent sheets and impose them on the template so that the dots cover all filled squares, but do not fall into any of the empty ones. You can overlay several points on any of the filled squares, but in general you should strive to use as few sheets as possible. To make it more interesting, I suggest making a bet: I pay $ 3 for the correct coverage of the 3 × 3 pattern, but you have to pay me $ 1 for each used sheet. Is this a good bet for you?
Before moving on, I must say that not every possible pattern can be closed according to such rules. Take an obvious example - no 3 × 3 pattern in which less than three squares are painted, you cannot close any combination of six transparent sheets with dots. But I promise that I will offer you only templates that can be closed with some combination of the available dot patterns; If I am mistaken in this, I will lose the money.
What will be the results of the game? If I give you a template marked above as “1 ″, then you will easily win: just choose the combinations a and b , which cover only all filled squares. You pay $ 2, and I give you 3. Pattern 2, in which all nine squares are painted, may seem like a daunting task. Obviously, it is impossible to close it with less than three sheets with patterns, because in total we need nine points; and it turns out that exactly three sheets are required. And in fact, there are two ways to cover a template with three sheets: a + d + e and b + c + f . Thus, this template gives us a break-even solution: you earn 3 dollars and spend 3 dollars.
Now we move on to pattern 3, in which there are filled squares and one is empty. It is clear that if you can close all nine squares with just three sheets, then we can close and eight, right? I recommend you to try. In fact, for a single suitable combination, four sheets are needed: b + d + e + f . Therefore, my proposal should not be accepted: I can always give you a template with only one empty square, and your loss will total $ 1.
In a second I will return to the gaming table, but first let me explain to you where this task came from. I once wrote about “evaluation intervals,” which led me to research the topic of permutation matrices. I will repeat what I have already said:
In the comments Barry Tsipra asks the following question:
I think now you can see the connection between the forms and my little game. The pattern of filled and empty squares is the format; sheets with dots denote permutation matrices; To maximize your winnings in the game (or minimize losses), you need to answer Barry's first question by finding the minimum number of permutations, the combination of which will give us a given format.
For 3 × 3 matrices, we can solve this problem by searching through the search, calculating the OR sum of all possible combinations of six permutation matrices 3 × 3 1, 2, 3, ..., 6 at the same time. On a recent flight, I managed to do it with paper and a pencil. In the end, I got the following results:

Some of the numbers on this card are easy to explain. Six ormats with only three unit elements are the permutation matrices themselves. There are six of them, because for three elements it is possible 3! = 6 permutations. There is no ormate with four single elements, and after a second thought, it can be understood: there can be no permutations that differ from each other by just one element. If you superimpose on each other any of the six sheets shown at the beginning of the article, you will get three, five, or six points, but never four.
On the other hand, we are not surprised that there is exactly one ormat with nine unit elements, and that it takes three permutations to create it. And there are nine ormats with eight unit elements that require performing OR for four permutations. These will be templates with one blank square, as shown in template 3 above.
Based on these results, I began to reflect on what I would get when I entered all 4 × 4 formats in the table.

It should turn out 4! = 24 templates with four unit elements, and only one with all units, created from the OR operation on four permutations. And there should be 16 ormats that require five permutations, namely 16 matrices with a single zero element. The last forecast seemed less obvious than the others.
I talked about a case with a single zero (or a single empty square) like this: in order to close 15 squares with sets of four points each, we need at least four sets, otherwise we simply don’t have enough points. Therefore, one of the optimal schemes covering all 16 squares without spaces and overlays will be a useful starting point. At this point I was tired of drawing billions of points, so I started working with coins.

In this scheme, each coin denomination forms a permutation: no two coins in pennies, five, ten or twenty-five cents are in the same column or in the same line. We successfully closed all the filled squares, but, unfortunately, closed one empty in the lower right corner. Such a scheme of coins is not an acceptable solution, but perhaps we can fix it?

By moving a penny from an empty square to another square of the same column, we solve one problem, but create another: now the penny layout is no longer a permutation — there are two pennies in the third line.

That is, now we have to shift one more penny to restore the property “one coin to one column and a row”. At the same time, the filled square will inevitably remain open. The only way we can close this free square is to add a fifth permutation. I ran out of coin denominations, so I use the popular brand of toroids for breakfast. Voila:

The movements I have made for this scheme are not unusual. If you try other templates, you can see for yourself that moving a penny covering an empty square to any other square in the fourth column (or fourth row) will result in exactly the same situation. Similarly, the result of the game will be the same if one empty square is located in any other place of the grid. And you can also start with a different set of source permutations (assuming they cover all the squares).
This coin-shifting exercise shows that we can close any 4 × 4 pattern with a single empty square combination of no more than five permutations, but how do we know what exactly five is needed? Perhaps there is some completely different scheme that can cope with just four permutations? Let's assume what this diagram might look like. It should differ in exactly one position from some other permutation scheme, completely covering the grid of 16 squares. But no two permutations can differ at one single point. That is, the argument that there cannot be a four-permutation scheme covering 15 squares is essentially the same as the argument that no 4 × 4 ormate pattern can cover only five squares.
This argument can be generalized to k × k matrices: for any integer k there must be at least k ormat schemes that cannot be closed less than k +1 permutations. But then we can make an even greater leap in reasoning: perhaps k +1 is the upper limit. Perhaps part of the answer to Barry's question is that no k × k format schemes require more than k +1 permutations. At some point, I even had “evidence” of this hypothesis. Then I wrote a program that does about the same work that I did with the points on the plane.
My program found 16 expected schemes of formats that require five permutations, but found many others. In general, she found 2,032 4 × 4 formats, which cannot be composed of less than five permutations. Then came a big surprise: the program also found 480 schemes requiring six permutations. Too much for my intended upper bound.
One of these 480 problematic ormats has the following form:
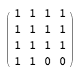
Looking at this pattern, I thought that I understood the reasons for the fallacy of my previous arguments. This matrix is exactly the same as the pattern with one zero, only two zeros! (I really think that this statement makes sense. Follow my reasoning.) Suppose we begin anew with a set of four permutations that completely cover the entire grid, including two empty squares.

Then we can open each empty square in the same way as we did with the rearrangement of coins, but we need to be careful that these two sets of displacements do not affect each other. (It doesn't make much sense to remove a penny from an empty square, and then immediately put a penny penny there.) Here is a strategy to open both empty squares, which preserves the permutation property “one in the column and row”:

When opening two empty squares, we will inevitably remove the coins from the two filled squares, which now need to be filled again. The most important thing here is that this problem cannot be eliminated by any single permutation, because the two open shaded squares are on the same line. To close both of these squares, we need two additional permutations.
Other ways of moving coins avoid placing two open squares in a single column or row, but they still fail all attempts to complete coverage with just five permutations. Try adding a ring to the diagram below. If you close both open blue squares, then you either close one of the empty squares, or two rings will be on the same line.

That is, we now understand that closing a 4 × 4 format requires six permutations. Does this mean that the upper bound in the general case can be equal to k +2, and not k +1? Or maybe the correct formula is 2 k –2? In support of the latter hypothesis, I propose to consider the following two formats, for which 8 and 10 permutations are required, respectively:
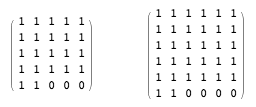
Having been deceived several times with the upper limit of the minimum coverage of the format, before offering another bet, I want to create a small space for errors. We already have direct evidence that it may take up to 2 k –2 permutations to cover the k × k ormate. Therefore, I will be generous and offer you 2k dollars for the right coverage, charging $ 1 for each permutation. If k = 3 or k = 4, then you can definitely make money on this deal. But will it be profitable for large k ? (Hint: I would play a game with real money rules.)
No one agrees to accept such a bet? Sorry - I have already spent my winnings.
Barry Tsipra, who asked about the minimum coverage of the format, sent me a wonderful letter:
Definitely consistent.
First, to answer a small question that Barry left open, I will show you many of the 16 permutations that successfully close his 7 × 7 “arrogant-triangular” matrix:
I found it a simple greedy search.
My own attempts to find the upper boundary were focused not on arrogant-triangular matrices, but on matrices, which I called “flags,” like this example for 7 × 7:

To properly cover this matrix, 16 permutations are also required. To see the reasons for this, try permutations through the columns of the matrix, starting from the left edge, choosing item 1 (and never 0) from each row from different columns. Because of the block of zeros in the upper left corner, the first three elements of each permutation must be in lines 4-7. That is, each permutation "occupies" three of the last four rows in the first three columns, and the remainder of the permutation can again fall into this interval of rows only once. It follows from this that each permutation can touch only one element in a 4 × 4 block of single elements in the right lower corner of the matrix, and for closing all single elements one needs at least 16 permutations. Proving that 16 permutations is enough is not so difficult.
This kind of analysis works for any odd k , and therefore we know that such matrices may be required
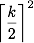
permutations. (For even k, the situation is less symmetrical, and I did not consider it in detail.)
These results give us the lower bound in the upper bound of the number of permutations that may be needed to close the orm k × k . But we have not proved that this is a real upper bound. Are there any other formats that require even more permutations? I think not, but do not forget that almost all of my hypotheses made in this article turned out to be incorrect.

Do you have a stack of transparent plastic sheets, in size and shape that coincide with the grid, on which the patterns of black dots are applied:

It is worth noting that in each of these patterns exactly three points, one point in each row and column. The six combinations shown are the only 3 × 3 grids with this property.
')
Your task is to assemble a subset of transparent sheets and impose them on the template so that the dots cover all filled squares, but do not fall into any of the empty ones. You can overlay several points on any of the filled squares, but in general you should strive to use as few sheets as possible. To make it more interesting, I suggest making a bet: I pay $ 3 for the correct coverage of the 3 × 3 pattern, but you have to pay me $ 1 for each used sheet. Is this a good bet for you?
Before moving on, I must say that not every possible pattern can be closed according to such rules. Take an obvious example - no 3 × 3 pattern in which less than three squares are painted, you cannot close any combination of six transparent sheets with dots. But I promise that I will offer you only templates that can be closed with some combination of the available dot patterns; If I am mistaken in this, I will lose the money.
What will be the results of the game? If I give you a template marked above as “1 ″, then you will easily win: just choose the combinations a and b , which cover only all filled squares. You pay $ 2, and I give you 3. Pattern 2, in which all nine squares are painted, may seem like a daunting task. Obviously, it is impossible to close it with less than three sheets with patterns, because in total we need nine points; and it turns out that exactly three sheets are required. And in fact, there are two ways to cover a template with three sheets: a + d + e and b + c + f . Thus, this template gives us a break-even solution: you earn 3 dollars and spend 3 dollars.
Now we move on to pattern 3, in which there are filled squares and one is empty. It is clear that if you can close all nine squares with just three sheets, then we can close and eight, right? I recommend you to try. In fact, for a single suitable combination, four sheets are needed: b + d + e + f . Therefore, my proposal should not be accepted: I can always give you a template with only one empty square, and your loss will total $ 1.
Some background information
In a second I will return to the gaming table, but first let me explain to you where this task came from. I once wrote about “evaluation intervals,” which led me to research the topic of permutation matrices. I will repeat what I have already said:
- The permutation matrix is a square matrix with one 1 in each column and each row; the remaining elements are 0.
- The ormat is the superposition of the permutation matrices formed by applying the Boolean function OR to the corresponding elements of the permutation matrices. For example:
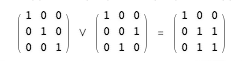
- Not all square matrices with elements (0,1) can be created by OR operations on permutation matrices, but there is an effective algorithm for determining whether a given matrix is an ormat.
- The total number of permutation paths in the format that can be passed through the unit elements of the matrix is equal to the permanent of the matrix. Definition of a permanent is considered a complex computational problem.
In the comments Barry Tsipra asks the following question:
A permanent tells us the maximum number of different permutations that can be summed up through OR to get a given format, but what will be the corresponding minimum number? In addition, how many different ways can a minimum be reached?
I think now you can see the connection between the forms and my little game. The pattern of filled and empty squares is the format; sheets with dots denote permutation matrices; To maximize your winnings in the game (or minimize losses), you need to answer Barry's first question by finding the minimum number of permutations, the combination of which will give us a given format.
For 3 × 3 matrices, we can solve this problem by searching through the search, calculating the OR sum of all possible combinations of six permutation matrices 3 × 3 1, 2, 3, ..., 6 at the same time. On a recent flight, I managed to do it with paper and a pencil. In the end, I got the following results:

Some of the numbers on this card are easy to explain. Six ormats with only three unit elements are the permutation matrices themselves. There are six of them, because for three elements it is possible 3! = 6 permutations. There is no ormate with four single elements, and after a second thought, it can be understood: there can be no permutations that differ from each other by just one element. If you superimpose on each other any of the six sheets shown at the beginning of the article, you will get three, five, or six points, but never four.
On the other hand, we are not surprised that there is exactly one ormat with nine unit elements, and that it takes three permutations to create it. And there are nine ormats with eight unit elements that require performing OR for four permutations. These will be templates with one blank square, as shown in template 3 above.
Based on these results, I began to reflect on what I would get when I entered all 4 × 4 formats in the table.

It should turn out 4! = 24 templates with four unit elements, and only one with all units, created from the OR operation on four permutations. And there should be 16 ormats that require five permutations, namely 16 matrices with a single zero element. The last forecast seemed less obvious than the others.
Trifle of pockets and breakfast cereals
I talked about a case with a single zero (or a single empty square) like this: in order to close 15 squares with sets of four points each, we need at least four sets, otherwise we simply don’t have enough points. Therefore, one of the optimal schemes covering all 16 squares without spaces and overlays will be a useful starting point. At this point I was tired of drawing billions of points, so I started working with coins.

In this scheme, each coin denomination forms a permutation: no two coins in pennies, five, ten or twenty-five cents are in the same column or in the same line. We successfully closed all the filled squares, but, unfortunately, closed one empty in the lower right corner. Such a scheme of coins is not an acceptable solution, but perhaps we can fix it?

By moving a penny from an empty square to another square of the same column, we solve one problem, but create another: now the penny layout is no longer a permutation — there are two pennies in the third line.

That is, now we have to shift one more penny to restore the property “one coin to one column and a row”. At the same time, the filled square will inevitably remain open. The only way we can close this free square is to add a fifth permutation. I ran out of coin denominations, so I use the popular brand of toroids for breakfast. Voila:

The movements I have made for this scheme are not unusual. If you try other templates, you can see for yourself that moving a penny covering an empty square to any other square in the fourth column (or fourth row) will result in exactly the same situation. Similarly, the result of the game will be the same if one empty square is located in any other place of the grid. And you can also start with a different set of source permutations (assuming they cover all the squares).
This coin-shifting exercise shows that we can close any 4 × 4 pattern with a single empty square combination of no more than five permutations, but how do we know what exactly five is needed? Perhaps there is some completely different scheme that can cope with just four permutations? Let's assume what this diagram might look like. It should differ in exactly one position from some other permutation scheme, completely covering the grid of 16 squares. But no two permutations can differ at one single point. That is, the argument that there cannot be a four-permutation scheme covering 15 squares is essentially the same as the argument that no 4 × 4 ormate pattern can cover only five squares.
This argument can be generalized to k × k matrices: for any integer k there must be at least k ormat schemes that cannot be closed less than k +1 permutations. But then we can make an even greater leap in reasoning: perhaps k +1 is the upper limit. Perhaps part of the answer to Barry's question is that no k × k format schemes require more than k +1 permutations. At some point, I even had “evidence” of this hypothesis. Then I wrote a program that does about the same work that I did with the points on the plane.
Went abroad
My program found 16 expected schemes of formats that require five permutations, but found many others. In general, she found 2,032 4 × 4 formats, which cannot be composed of less than five permutations. Then came a big surprise: the program also found 480 schemes requiring six permutations. Too much for my intended upper bound.
One of these 480 problematic ormats has the following form:

Looking at this pattern, I thought that I understood the reasons for the fallacy of my previous arguments. This matrix is exactly the same as the pattern with one zero, only two zeros! (I really think that this statement makes sense. Follow my reasoning.) Suppose we begin anew with a set of four permutations that completely cover the entire grid, including two empty squares.

Then we can open each empty square in the same way as we did with the rearrangement of coins, but we need to be careful that these two sets of displacements do not affect each other. (It doesn't make much sense to remove a penny from an empty square, and then immediately put a penny penny there.) Here is a strategy to open both empty squares, which preserves the permutation property “one in the column and row”:

When opening two empty squares, we will inevitably remove the coins from the two filled squares, which now need to be filled again. The most important thing here is that this problem cannot be eliminated by any single permutation, because the two open shaded squares are on the same line. To close both of these squares, we need two additional permutations.
Other ways of moving coins avoid placing two open squares in a single column or row, but they still fail all attempts to complete coverage with just five permutations. Try adding a ring to the diagram below. If you close both open blue squares, then you either close one of the empty squares, or two rings will be on the same line.

That is, we now understand that closing a 4 × 4 format requires six permutations. Does this mean that the upper bound in the general case can be equal to k +2, and not k +1? Or maybe the correct formula is 2 k –2? In support of the latter hypothesis, I propose to consider the following two formats, for which 8 and 10 permutations are required, respectively:

Another bet
Having been deceived several times with the upper limit of the minimum coverage of the format, before offering another bet, I want to create a small space for errors. We already have direct evidence that it may take up to 2 k –2 permutations to cover the k × k ormate. Therefore, I will be generous and offer you 2k dollars for the right coverage, charging $ 1 for each permutation. If k = 3 or k = 4, then you can definitely make money on this deal. But will it be profitable for large k ? (Hint: I would play a game with real money rules.)
No one agrees to accept such a bet? Sorry - I have already spent my winnings.
Barry Tsipra, who asked about the minimum coverage of the format, sent me a wonderful letter:
I will give a brief outline of the short hypothesis (in fact, just a hunch) that the behavior in the “worst case”, in terms of the minimum number of permutations necessary to obtain a given ormat, occurs for the following form, shown here for k = 7:
In order not to violate the existing terminology of matrices, I will call any (square) matrix of this type, i.e. such, all elements of which below the main subdiagonal are 0, “arrogant triangular”. I can show (and do it!) That this arrogant-triangular ormat with k = 7 requires (at least) 16 permutations, and that starting from this value of k, the number increases dramatically. Therefore, personally, I definitely would not accept your bid of 2 k dollars.
The trick is to treat each ormat as a “shadow” of what I will call an “addmat” (addmat). Let P 1, P 2, ..., Pr be the permutation matrices k × k ; then their addmat will be the usual result of addition: S = P 1 + P 2 + ... + Pr whose elements are positive integers, where one or more components of the permutations have 1, otherwise they are zero. The corresponding format is obtained by replacing each of the nonzero elements by 1 with the preservation of zero elements. In this sense, the unit elements of the form are the “shadows” of the positive elements of the admat.
The most important thing is that addmats have a pleasant little property that their shadow does not have: all sums of a row and a column of addmat elements are equal to the number of permutations r that created them.
And now let's think together. The above example of an arrogant-triangular ormat (with k = 7) should be obtained from the addmat of the form
where a , b and all * are positive numbers. In particular, each * has a value of at least 1. Since all sums of rows and columns must be the same, the sum of a + b must be equal to b and all six * above them. Consequently, a has a value of at least 6. Similarly, the sum of a + b must be equal to the sum of a and all six * above it, that is, the value of b is also not less than 6. Therefore, a + b is not less than 12, that is, OR- sum, creating a given format requires at least 12 permutations.
These arguments can be generalized to an arbitrary k , that is, we get not just “direct evidence” that it can take up to 2 k –2 permutations for k × k ormate — this is a strict proof! But we can immediately improve it, at least for specific cases. If we try to do just 12 permutations for this arrogant-triangular ormata, then we will quickly have a problem. Obviously, we need a = b = 6, and, therefore, all * above them are ones (to get the total of 12 in this column). That is, we have an addmat
in which I want to draw your attention to the element marked as "@". To make the sum of its row equal to 12, we need @ = 10. But this means that the sum of its column (with five * above it) is not less than 15. But this can not be! So, we have to try to pick up large values of a and / or b , that is, to create this addmat we need more permutation matrices.
It turns out that we cannot satisfy the condition of the sum of rows and columns until we get to a = b = 8. I will not explain all the steps, but simply show the penultimate possible combination, a = 7, b = 8. The best you can hope in this case:
Notice that in the last two columns I gave as much “weight” as possible so that they were as close as possible to 7 and 8, and you could use the smallest possible value (10) as an element with five positive elements above it. Thanks to this, the last three lines and the three right lines have the same amount (15), but now there is a problem with a column with item 12: its amount is not less than 16. So, I repeat, we are at a dead end. We can avoid contradiction only with the following attempt:
Finally, all sums of rows and columns of the matrix are the same. It is worth considering that this may or may not be a real addmat of the set of 16 permutation matrices. I suspect that this is still addmat, but I do not want to check it. All that we know is that it satisfies the necessary condition of the addmat, namely, all sums of rows and columns are the same. (It would be great if this were a sufficient condition, but something tells me that it is not.)
This example, which can be faithfully reproduced for large values of k , makes us understand that the player who offers the game is not only winnings at the rate of 2 k dollars. but with (2 k + 2) dollars and above. I experimented a bit with this and made sure that the number of permutation matrices will be much more than 2 k with k = 10. If I did everything correctly, then you will need 24 permutations (and possibly more if the analysis of the arrogant-triangular matrix shows us that it is not a real addmat). I am absolutely convinced that, after careful consideration, analysis can be simplified to a convenient and elegant proof. I'm just not sure if I have already made mistakes and built a house of cards from reasoning.
Does everything said to what you came to?
Definitely consistent.
First, to answer a small question that Barry left open, I will show you many of the 16 permutations that successfully close his 7 × 7 “arrogant-triangular” matrix:
{1,2,3,4,5,6,7} {2,1,4,3,6,7,5} {1,3,2,5,4,7,6} {1,3,4,2,6,5,7}
{2,3,1,5,6,4,7} {1,2,3,5,6,7,4} {1,2,4,5,3,6,7} {1,2,4,5,6,3,7}
{1,2,4,5,6,7,3} {1,3,4,5,2,6,7} {1,3,4,5,6,2,7} {1,3,4,5,6,7,2}
{2,3,4,1,5,6,7} {2,3,4,5,1,6,7} {2,3,4,5,6,1,7} {2,3,4,5,6,7,1}I found it a simple greedy search.
My own attempts to find the upper boundary were focused not on arrogant-triangular matrices, but on matrices, which I called “flags,” like this example for 7 × 7:

To properly cover this matrix, 16 permutations are also required. To see the reasons for this, try permutations through the columns of the matrix, starting from the left edge, choosing item 1 (and never 0) from each row from different columns. Because of the block of zeros in the upper left corner, the first three elements of each permutation must be in lines 4-7. That is, each permutation "occupies" three of the last four rows in the first three columns, and the remainder of the permutation can again fall into this interval of rows only once. It follows from this that each permutation can touch only one element in a 4 × 4 block of single elements in the right lower corner of the matrix, and for closing all single elements one needs at least 16 permutations. Proving that 16 permutations is enough is not so difficult.
This kind of analysis works for any odd k , and therefore we know that such matrices may be required
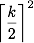
permutations. (For even k, the situation is less symmetrical, and I did not consider it in detail.)
These results give us the lower bound in the upper bound of the number of permutations that may be needed to close the orm k × k . But we have not proved that this is a real upper bound. Are there any other formats that require even more permutations? I think not, but do not forget that almost all of my hypotheses made in this article turned out to be incorrect.
Source: https://habr.com/ru/post/350210/
All Articles




