Programming Languages ​​for a Quantum Computer

The prototype of the nucleus of an ionic quantum computer. Ion Quantum Technology Group , University of Sussex

Quantum computers from time to time get into the media. You hear about how people step by step approaching their creation, although for most development of quantum computing remains a strange and mysterious art.

Fortunately, to solve this problem, there are excellent projects that attract the attention of a wide audience. For example, several years ago, IBM gave anyone the opportunity to connect to a 5-qubit computer. The project registered 70,000 people.

However, the quantum computing industry is still in its infancy. Although many prototypes have already been created, they cannot do what a regular laptop cannot handle. The necessary hardware does not yet exist, but we have something else to study - quantum programming languages.

A journey into the world of quantum computing is accessible to everyone and resembles the study of any ordinary language in normal programming.

Quantum computing

To dive into the world of quantum computing, you do not need to keep a quantum computer at home. There are projects that provide access to real quantum devices, but simple quantum programs can be easily modeled on a regular laptop.

Before tackling programs, let's recall the basic things about quantum computing. And here will help us the article by Brian Hayes " Programming Your Quantum Computer ".

A conventional computer is based on bits: it comes with variables that have only two possible values. We often call them 0 and 1, although in the context of Boolean algebra we can call them "True" and "False."

Bits can perform simple boolean operations, such as NOT, AND, and OR. Any variable that is more complex than a bit (for example, int or float) is simply a set of bits.

Quantum computers are based on quantum bits or qubits. They also have two possible meanings, which we can call 0 and 1. But the laws of quantum mechanics also allow other values, which we call superposition states.

In a sense, superposition states are values ​​that exist between extremes 0 and 1. We can think of a qubit as a sphere, with 0 and 1 located at opposite poles. Superposition states are all other possible points on the surface.

The point is not that the qubit can have an intermediate value, for example, 0.63; when a qubit state is measured, the result is always 0 or 1. But during the calculation, the qubit can act as if it were a mixture of states — for example, 63% of zero and 37% of the unit.

Another key aspect of qubit behavior is interference, a phenomenon well known in wave physics. When two waves overlap, they can reinforce each other (if the peaks and wave-like decay coincide), or they can level each other (if the waves do not correspond to the phase). Mathematically, the intensity of the combined waves at any point is determined by the square of the sum of the individual wave amplitudes. When two amplitudes have the same sign, the interference is constructive; when one amplitude is positive and the other is negative, the resulting destructive interference gives less intensity than that of a single wave.

Like waves, 0 and 1 qubit states have amplitudes that can be either positive or negative. Depending on the amplitude signs, quantum interference can either increase or decrease the likelihood that a certain state will be observed when we measure the state of the qubit.

Interference plays a role in all interesting algorithms for quantum computers, that is, algorithms that can allow such a machine to be superior to a classic computer. The general idea to organize the evolution of a quantum system is to ensure that erroneous answers are suppressed by destructive interference, and the correct answers are amplified by constructive interference. Thus, algorithms use the form of parallelism, unique to quantum systems.

One of the last aspects of quantum oddity is entanglement. You cannot change one qubit within a quantum register, leaving the rest unchanged. To begin with, each function computed by a quantum system must be completely reversible. If the machine receives at input A to output the result B, then it should be possible to restore A in the presence of B.

Each function must have the same number of inputs and outputs. At one stroke, this rule prohibits most of the arithmetic. The usual addition algorithm, for example, is irreversible. You can add 3 and 4 to get 7, but you cannot “disconnect” 7 to restore the original 3 and 4.

Another prohibition in quantum computing is copying a qubit (this principle is called the theorem on the prohibition of cloning ). Also, you cannot arbitrarily install or reload qubits in the middle of a computation. Attempting to do this would destroy quantum superposition.

Taken together, restrictions on qubit operations imply that any quantum program must have a chimney architecture — information travels straight from one end to the other. It is especially important that in the program structure there can be no cycles where control is transferred back to an earlier point.

The answer to these difficulties is found in quantum programming languages. In fact, quantum computers are hybrid devices: partially quantum and partially classical computers. The use of ordinary computer elements is necessary for processing inputs and outputs in order to interact with external applications. Thus, in one program, you can combine a classic code and a quantum code.

Open Quantum Assembly Language (OpenQASM)

The OpenQASM source code was released as part of the IBM Quantum Information Software Kit (QISKit) software for use with the Quantum Experience quantum computing platform. OpenQASM has common features with specialized programming languages ​​(such as Verilog) used to describe the structure and behavior of electronic circuits.

QASM programs actually always start the same way: we define all the bits that we need — both quantum and normal. Below is an example of the OpenQASM source code. The program adds two four-bit numbers.

OPENQASM 2.0; include "qelib1.inc"; gate majority a,b,c { cx c,b; cx c,a; ccx a,b,c; } gate unmaj a,b,c { ccx a,b,c; cx c,a; cx a,b; } qreg cin[1]; qreg a[4]; qreg b[4]; qreg cout[1]; creg ans[5]; //    xa[0]; // a = 0001 xb; // b = 1111 //  a  b,    b majority cin[0],b[0],a[0]; majority a[0],b[1],a[1]; majority a[1],b[2],a[2]; majority a[2],b[3],a[3]; cx a[3],cout[0]; unmaj a[2],b[3],a[3]; unmaj a[1],b[2],a[2]; unmaj a[0],b[1],a[1]; unmaj cin[0],b[0],a[0]; measure b[0] -> ans[0]; measure b[1] -> ans[1]; measure b[2] -> ans[2]; measure b[3] -> ans[3]; measure cout[0] -> ans[4]; 

Q #

The high-level programming language Q # eliminates the need to have deep knowledge in quantum physics. For those interested in a language textbook, information is provided on the basic concepts of quantum computing, covering vector and matrix mathematics, qubits, Dirac notation , Pauli principle, and quantum schemes .

 operation Teleport(msg : Qubit, there : Qubit) : () { body { using (register = Qubit[1]) { let here = register[0]; H(here); CNOT(here, there); CNOT(msg, here); H(msg); if (M(msg) == One) { Z(there); } if (M(here) == One) { X(there); } } } } 

Script Teleportation.qs from the tutorial on Q #. A tutorial is available here.

Q # does not look like most other programming languages, and is somewhat similar to C #.

The Quantum Development Kit is provided free of charge with detailed installation instructions and introductory training programs. Q # is compiled on a Visual Studio quantum simulator, simulating a 32-qubit quantum processor. The simulator can simulate up to 40 qubits.

If you follow the tutorial from Microsoft, then the learning process will go from observing entangled states from two qubits to modeling quantum teleportation.

LIQUi (Language-Integrated Quantum Operations)

The LIQUi platform, created by the Quantum Architectures and Computation Group team at Microsoft Research, includes a programming language, optimization and scheduling algorithms, and several quantum simulators. LIQUi can be used to translate a quantum algorithm written in the form of a high-level program in the F # language from the .NET Framework family into low-level commands for a quantum computer.

LIQUi allows you to simulate up to 30 qubits on a single machine with 32 GB of RAM. The platform can be used to define, execute, and display quantum graphics in various graphic formats. With LIQUi, you can simulate a simple quantum teleportation, Shore's factorization algorithm, quantum associative memory, quantum linear algebra.

 operation TeleportClassicalMessage(message : Bool) : Bool { body { mutable measurement = false; using (register = Qubit[2]) { //   ,     . let msg = register[0]; let there = register[1]; //  ,    . if (message) { X(msg); } Teleport(msg, there); //  . if (M(there) == One) { set measurement = true; } ResetAll(register); } return measurement; } } 

As you can see from the example above, LIQUi is very similar to Q #.

Quantum Computation Language (QCL)

QCL, or Quantum Computation Language, was created by Bernhard Omer in 1998. The development of the language continues today: there is an emulator that allows you to run quantum programs on a classical computer. Of course, the emulator cannot provide acceleration of quantum parallelism; on the other hand, it offers the programmer some useful functions, such as commands for checking the internal state of qubits (which is extremely difficult to do on real quantum equipment).

QCL borrows C and Java syntax, which are sometimes described as “imperative” languages, because they rely on direct commands to set and reset variable values. Such commands are usually forbidden in quantum computing, so the main parts of the QCL program only work on classic hardware. The quantum system serves as an “oracle”, answering questions that can be asked in a format suitable for qubit calculations. Each request to an oracle must have the required chimney architecture, but it can be built into the cycle in an external classical context.

Fragment of code created in QCL (Discrete Fourier Transform):

 operator dft(qureg q) { const n=#q; int i; int j; for i=1 to n { for j=1 to i-1 { V(pi/2^(ij),q[ni] & q[nj]); } H(q[ni]); } flip(q); } 

The discrete Fourier transform is a crucial step in the Shor factorization algorithm. In Shor’s algorithm, the number to be factorized is considered as a wave-like, periodic signal. If N has coefficients u and v, then N consists of u repetitions v or v repetitions u. Shor's algorithm uses quantum parallelism to find the period of such repetitions, although the process is not as simple and straightforward as it may seem in the example above.

Quipper

The language was created by a team of authors under the direction of Peter Selinger. Quipper is designed for the same programming tasks as QCL, but has a different structure and appearance. The language is implemented as a Haskell extension, which uses a functional rather than an imperative way of expression.

Consider the classic quantum teleportation. It includes two sides - Alice and Bob. Alice's goal is to teleport the qubit q to Bob. Alice and Bob should have access to qubits from a confused pair (a, b). We can think about the role of Alice in terms of a function that introduces two qubits q and a. The output of the function will be a pair of classic bits created by Alice:

 alice :: Qubit -> Qubit -> Circ (Bit,Bit) alice qa = do a <- qnot a 'controlled' qq <- hadamard q (x,y) <- measure (q,a) return (x,y) 

More information can be found in the document “ An Introduction to Quantum Programming in Quipper ”.

And here is an interesting example of raising to the 17th degree, by raising x to the 16th degree by the built-in squaring procedure and by multiplying x and x ^ 16:

 o4_POW17 :: QIntTF -> Circ (QIntTF,QIntTF) o4_POW17 = box "o4" $ \x -> do comment_with_label "ENTER: o4_POW17" x "x" (x, x17) <- with_computed_fun x (\x -> do (x,x2) <- square x (x2,x4) <- square x2 (x4,x8) <- square x4 (x8,x16) <- square x8 return (x,x2,x4,x8,x16)) (\(x,x2,x4,x8,x16) -> do (x,x16,x17) <- o8_MUL x x16 return ((x,x2,x4,x8,x16),x17)) comment_with_label "EXIT: o4_POW17" (x,x17) ("x","x17") return (x, x17) 

Quipper is a compiler, not an interpreter; he translates the complete program at a time, rather than following instructions one after the other. The compiler output consists of quantum circuits: networks of interconnected, reversible logic gates. The circuit may take the form of an electrical circuit, but it also represents a sequence of instructions, ready for execution with the help of suitable quantum equipment or a simulator.

Quipper, like QCL, automatically generates schemas from high-level source semantic constructs.

Other approaches

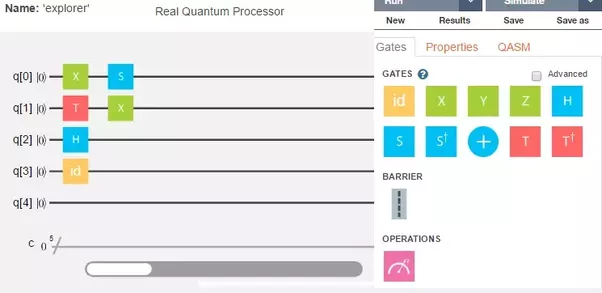
The multi-colored squares tell IBM's five quantum bits what to do. By dragging and dropping, you can create your own quantum calculations.

The IBM Quantum Experience project provides an opportunity for everyone to run an experimental program on a real quantum computer. Working with the IBM programming language is similar to the process of writing music using an application. A programmer can simply drag quantum objects into a specific area to write a program.

Quantum Computing Playground is a WebGL Chrome experiment that allows you to simulate working with a quantum computer in a browser window. It has its own Qscript scripting language with debugging and 3D quantum visualization features. A quantum computing platform can effectively simulate quantum registers of up to 22 qubits.

The Python QISKit SDK includes several tools that IBM Q engineers provided to illustrate quantum programming purposes. In particular, the SDK shows how you can complete several tasks for complex experiments. As the name implies, QISKit allows developers to explore a quantum computer using Python.

Qbsolv is an open source project for working with qubbles of the D-Wave quantum processor (suitable only for computers of this company).

There are already dozens of quantum programming languages ​​(and simulators), but they all work in a virtual machine. IBM Q is probably the only project that offers access to a real quantum computer. However, in order to begin to engage in "quantum programming", it is not at all necessary to have access to a real advanced device. Already, one can not only study the work of promising quantum algorithms, but also create working applications, such as games. But that's another story.

Sources:

Even You Can Help Build a Quantum Computer
Quipper: Quantum Computers
Quantum Programming Language
How to program a quantum computer
Structured Quantum Programming
QCL - A Programming Language for Quantum Computers