Asynchronous circuits. Calculation of logical functions directly on the event graph. Part 1
In the last article, I already mentioned the existence of alternative methods for calculating logical functions. In this article I will begin to acquaint you with the calculation of logical functions directly from the event description (for example, STG). There is no need to confuse event descriptions with descriptions via states (an example is a diagram of changes). The method itself was born for the synthesis of asynchronous circuits, but if desired, it can be used in the synthesis of synchronous circuits. Distinctive features of the method are: 1) a complete rejection of the use of such a concept as a state (when explaining, I will certainly refer to this concept); 2) a significant reduction in computing due to the use of information about neighboring states. In computer calculations, this allows you to significantly reduce the computation time and radically solve the problem of lack of memory in the explosion of states. With manual calculations, the method allows, with sufficient skill, to operate with behaviors with hundreds of signals. This, of course, is about calculating the minimum functions.
To begin, consider the simplest behavior: sequential, cyclic, each signal switches exactly 2 times per cycle. Behavior will be represented as a string, direction from left to right. Ellipsis indicates that a sequence of switching signals is possible in this place.
Let's start with how the state looks on the graph.
')

A state is a dot (red) between two events. In this case, it is: a = 0, b = 1, c = 0, d = 1. In STG, a state is a set of tagged playlists.
Now let's see how a simple implicant looks on the graph. We will consider the conjunction (function I).
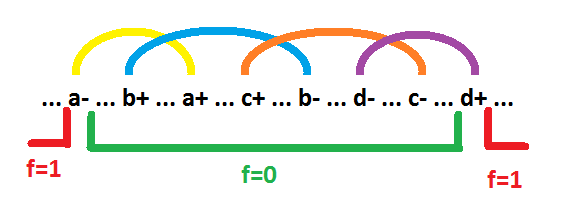
The green is underlined the zone where the implicant is 0. The red is the underlined zone where the implicant is 1. In this zone, all the signals defining the implicant are constant. All space outside this zone is a chain of interceptions. The links of this chain (shown above the graph above) are formed by switching signals that form the implicant. Each link is a pair of switchings of a single signal. The signal forming the link on the states inside this link maintains the value of implicants equal to 0. The zone of ones (and accordingly the zone of zeros) may be intermittent. But so far this possibility is not necessary to consider. Under the accepted conditions, such a structure of the interception chain for simple implicants is the only possible one. For example, if the c + event were located to the left of the a + event, then the b signal could be removed from the implicants. In the following, by implicant we will mean the zone of units of this implicant. Extreme events of the chain of interceptions will be called the boundaries of the implicants. In the figure, event d + is the left border, event a- is the right border. It remains to find out which signals enter the implicant with inversion, and which without inversion. If the link starts with "-" events, then the signal enters the implicant without inversion (in the figure signals a and d). If the link starts with a "+" event, then the signal enters the implicant with inversion (in the figure signals b and c). As a result, the figure shows the behavior of the implicants a *! B *! C * d.
We now turn to the construction of implicants. To begin with, we will answer the question: what is the main characteristic of implicants in terms of calculating logical functions? It would seem that these are the variables (signals) that make up this implicant. But in fact, the main characteristic of implicants is its location on the behavior graph (as we agreed on the location of the unit zone). And the signals that make up the implicant are the means to achieve the desired location. That is, the process of building implicants is the calculation of the necessary signals in order to locate the implicants in the right place on the graph. Now the question arises: how to set the location of the future location of implicants? The location of the implicants will be set by 3 points (states).

Point 2 is the state on which the implicant must necessarily take the value 1. Point 1 and 3 are extreme states on which the implicant can take the value 1. That is, the implicant must contain point 2 and can be expanded up to points 1 and 3. Position the left border is indifferent, the right border should be moved as far as possible from point 2. Points 1 and 3 can coincide with point 2 (separately, but not together at once).
The process of building implicants is a sequential search for signals - links of the interception chain. This process is more convenient to lead from right to left (the reasons for this will be explained later). The search begins between points 1 and 2. And ends when the link falls between points 2 and 3. The impossibility of building such a chain of interceptions means only one thing: the behavior contains a CSC conflict. Since we are looking for implicants for the minimal function, there are two factors that can conflict with each other: the number of variables in the implicant (i.e. links) and the length of implicants (the set of states that it covers). Therefore, the links are selected the longest. In addition to the latter, which is selected as short as possible. It is also necessary to take into account the moment that the last link can be replaced by a chain of shorter links. In this case, the length of the implicants may increase.
Now I will describe an algorithm for computing simple implicants covering point 2. The algorithm uses 2 sets as memory: the set of candidates for the current link (set P) and the set of candidates for the next link (set N). The maximum number of members of these sets is equal to the number of signals. Initially the sets are empty.
Step 1. We take into consideration the event located to the left of point 2.
Step 2. If the event under consideration is located to the left of point 1, then a) the signal corresponding to the event in question is added to the set P, b) we proceed to the consideration of the previous event.
Step 3. If the event in question is located to the right of point 3, then go to step 15.
Step 4. If the event in question is located to the left of point 1, then a) if the signal corresponding to the event in question belongs to the set N, then we exclude this signal from this set, otherwise we add this signal to this set; b) if the set N is empty (this means CSC conflict), then we exit the algorithm; c) the set P is made equal to the set N, d) the set N is made empty, e) proceed to the consideration of the preceding event, e) go to step 3.
Step 5. If the signal corresponding to the event under consideration belongs to the set N, then a) we exclude this signal from this set, b) proceed to the consideration of the preceding event, c) proceed to step 3.
Step 6. If the signal corresponding to the event under consideration does not belong to the set P, then a) add this signal to the set N, b) proceed to the consideration of the preceding event, c) proceed to step 3.
Step 7. Remove the signal corresponding to the event in question from the set P.
Step 8. If the set P is not empty, then a) go to the consideration of the preceding event, b) go to step 3.
Step 9. The signal corresponding to the event in question is added to the implicant as a variable.
Step 10. If the set N is empty (CSC conflict), then we exit the algorithm.
Step 11. Set P to be equal to N.
Step 12. Set N to be empty.
Step 13. We proceed to the consideration of the previous event.
Step 14. Go to step 3.
Step 15. If the signal corresponding to the event in question does not belong to the set P, then a) proceed to the consideration of the preceding event, b) repeat step 15.
Step 16. The signal corresponding to the event in question is added to the implicant as a variable.
Step 17. Implicant built. The completion of the algorithm.
As can be seen, the complexity of the algorithm for calculating simple implicants by the event graph (under the accepted conditions) is proportional to the number of events in the graph. The algorithm also requires almost no memory costs.
This algorithm is configured to calculate implicants with the least number of variables. To obtain implicants with a large number of variables, but covering more states, a slight improvement is necessary. It is necessary to memorize the last signal removed from the set P. And also all signals removed from the set N after this. After the algorithm comes to step 15, you need to restore the deleted and stored signals in the set N, add the last signal removed from the set P to the implicant and continue the examination from the event after which the signal from the set P was removed last time. In this way, all extremals can be found. To be continued.
To begin, consider the simplest behavior: sequential, cyclic, each signal switches exactly 2 times per cycle. Behavior will be represented as a string, direction from left to right. Ellipsis indicates that a sequence of switching signals is possible in this place.
Let's start with how the state looks on the graph.
')

A state is a dot (red) between two events. In this case, it is: a = 0, b = 1, c = 0, d = 1. In STG, a state is a set of tagged playlists.
Now let's see how a simple implicant looks on the graph. We will consider the conjunction (function I).
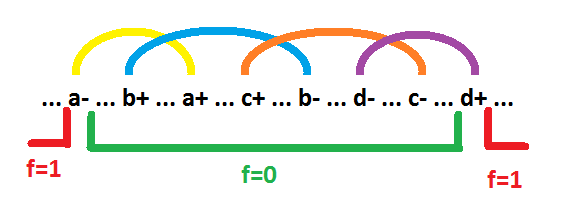
The green is underlined the zone where the implicant is 0. The red is the underlined zone where the implicant is 1. In this zone, all the signals defining the implicant are constant. All space outside this zone is a chain of interceptions. The links of this chain (shown above the graph above) are formed by switching signals that form the implicant. Each link is a pair of switchings of a single signal. The signal forming the link on the states inside this link maintains the value of implicants equal to 0. The zone of ones (and accordingly the zone of zeros) may be intermittent. But so far this possibility is not necessary to consider. Under the accepted conditions, such a structure of the interception chain for simple implicants is the only possible one. For example, if the c + event were located to the left of the a + event, then the b signal could be removed from the implicants. In the following, by implicant we will mean the zone of units of this implicant. Extreme events of the chain of interceptions will be called the boundaries of the implicants. In the figure, event d + is the left border, event a- is the right border. It remains to find out which signals enter the implicant with inversion, and which without inversion. If the link starts with "-" events, then the signal enters the implicant without inversion (in the figure signals a and d). If the link starts with a "+" event, then the signal enters the implicant with inversion (in the figure signals b and c). As a result, the figure shows the behavior of the implicants a *! B *! C * d.
We now turn to the construction of implicants. To begin with, we will answer the question: what is the main characteristic of implicants in terms of calculating logical functions? It would seem that these are the variables (signals) that make up this implicant. But in fact, the main characteristic of implicants is its location on the behavior graph (as we agreed on the location of the unit zone). And the signals that make up the implicant are the means to achieve the desired location. That is, the process of building implicants is the calculation of the necessary signals in order to locate the implicants in the right place on the graph. Now the question arises: how to set the location of the future location of implicants? The location of the implicants will be set by 3 points (states).

Point 2 is the state on which the implicant must necessarily take the value 1. Point 1 and 3 are extreme states on which the implicant can take the value 1. That is, the implicant must contain point 2 and can be expanded up to points 1 and 3. Position the left border is indifferent, the right border should be moved as far as possible from point 2. Points 1 and 3 can coincide with point 2 (separately, but not together at once).
The process of building implicants is a sequential search for signals - links of the interception chain. This process is more convenient to lead from right to left (the reasons for this will be explained later). The search begins between points 1 and 2. And ends when the link falls between points 2 and 3. The impossibility of building such a chain of interceptions means only one thing: the behavior contains a CSC conflict. Since we are looking for implicants for the minimal function, there are two factors that can conflict with each other: the number of variables in the implicant (i.e. links) and the length of implicants (the set of states that it covers). Therefore, the links are selected the longest. In addition to the latter, which is selected as short as possible. It is also necessary to take into account the moment that the last link can be replaced by a chain of shorter links. In this case, the length of the implicants may increase.
Now I will describe an algorithm for computing simple implicants covering point 2. The algorithm uses 2 sets as memory: the set of candidates for the current link (set P) and the set of candidates for the next link (set N). The maximum number of members of these sets is equal to the number of signals. Initially the sets are empty.
Step 1. We take into consideration the event located to the left of point 2.
Step 2. If the event under consideration is located to the left of point 1, then a) the signal corresponding to the event in question is added to the set P, b) we proceed to the consideration of the previous event.
Step 3. If the event in question is located to the right of point 3, then go to step 15.
Step 4. If the event in question is located to the left of point 1, then a) if the signal corresponding to the event in question belongs to the set N, then we exclude this signal from this set, otherwise we add this signal to this set; b) if the set N is empty (this means CSC conflict), then we exit the algorithm; c) the set P is made equal to the set N, d) the set N is made empty, e) proceed to the consideration of the preceding event, e) go to step 3.
Step 5. If the signal corresponding to the event under consideration belongs to the set N, then a) we exclude this signal from this set, b) proceed to the consideration of the preceding event, c) proceed to step 3.
Step 6. If the signal corresponding to the event under consideration does not belong to the set P, then a) add this signal to the set N, b) proceed to the consideration of the preceding event, c) proceed to step 3.
Step 7. Remove the signal corresponding to the event in question from the set P.
Step 8. If the set P is not empty, then a) go to the consideration of the preceding event, b) go to step 3.
Step 9. The signal corresponding to the event in question is added to the implicant as a variable.
Step 10. If the set N is empty (CSC conflict), then we exit the algorithm.
Step 11. Set P to be equal to N.
Step 12. Set N to be empty.
Step 13. We proceed to the consideration of the previous event.
Step 14. Go to step 3.
Step 15. If the signal corresponding to the event in question does not belong to the set P, then a) proceed to the consideration of the preceding event, b) repeat step 15.
Step 16. The signal corresponding to the event in question is added to the implicant as a variable.
Step 17. Implicant built. The completion of the algorithm.
As can be seen, the complexity of the algorithm for calculating simple implicants by the event graph (under the accepted conditions) is proportional to the number of events in the graph. The algorithm also requires almost no memory costs.
This algorithm is configured to calculate implicants with the least number of variables. To obtain implicants with a large number of variables, but covering more states, a slight improvement is necessary. It is necessary to memorize the last signal removed from the set P. And also all signals removed from the set N after this. After the algorithm comes to step 15, you need to restore the deleted and stored signals in the set N, add the last signal removed from the set P to the implicant and continue the examination from the event after which the signal from the set P was removed last time. In this way, all extremals can be found. To be continued.
Source: https://habr.com/ru/post/349756/
All Articles