Haskell. The problem of the sages and caps

Three wise men argued which of them is the wisest. To find out the truth, everyone put a random color cap on his head. Every sage sees the colors of the caps of his opponents, but does not see his own. The winner is the one who can determine the color of his cap.



It so happened that all three pulled the caps white. A passerby passing by tells them: “a white cap is put on one of you”. After some time, the smartest of the wise men exclaimed: “I have a white cap !!!”.



How did he figure it out?

There is a certain sequence of reasoning that led our sage to the right answer. We will try to model this reasoning.

How did he figure it out?

This problem can be formulated for any number of wise men. Let's consider the easiest option.

')

Two wise men sit, each wearing a white cap. Both know that there is at least one white cap. Then one of the wise men argues: “if I had a cap of any non-white on me, then my opponent would have guessed that there is a white cap on it. But he is silent. So white cap on me! "



When there are three wise men, one of them argues like this: “If I’m not wearing a white cap, the other sage will think so. ... (further there are arguments from the problem about two wise men) ... one of them would have guessed that there is a white cap on it. But they both are silent. So my first guess is wrong, and I have a white cap! ”



By induction, we can extend this reasoning to any number of sages. Further in the article, we will model the situation with the three wise men.

Task statement

In our original formulation, the problem is not completely correct. It is not clear how much time must pass to conclude that the other sage did not guess the color of his cap. Let me rephrase the problem more correctly.

There are three wise men. Each is wearing a cap, either black or white. Everyone knows the colors of his opponents, but does not know his own.



On the first day, they are told that there is at least one white cap. They think all day and vote at the end of the day independently of each other. They give one of two possible results: “I know my color,” “I don't know my color.”



On the second day, they become acquainted with the "voting results" of each of the opponents. Then they think again all day and vote again at the end of the day.



and so on.



Question. How will each of the sages vote on each of the days under different initial conditions?

Code

To begin with we will describe our main types with which we will work.

data Color = Black | White deriving (Show, Eq) type State = [Color] fullState :: [State] fullState = do c1 <- [Black, White] c2 <- [Black, White] c3 <- [Black, White] return [c1, c2, c3] type StateInfo a = State -> a stateInfoColor :: Int -> StateInfo Color stateInfoColor i state = state !! i stateInfoAnyWhite :: StateInfo Bool stateInfoAnyWhite state = or $ map (\c -> c == White) state 

The state of our world (which cap is worn) is described using the State type. In the variable fullState we store a list of all possible states.



The StateInfo type describes some information that we can calculate from the state of the world. For example, using stateInfoColor we can isolate the color of the cap for a particular sage. And using stateInfoAnyWhite, we calculate whether the statement that all caps are white is true for a given state.



Next come the more complex structures.

 type Knowledge = State -> (State -> Bool) knowledgeAbout :: (Eq a) => StateInfo a -> Knowledge knowledgeAbout stateInfo state = let info = stateInfo state in \s -> stateInfo s == info knowledgeIsTrue :: StateInfo Bool -> Knowledge knowledgeIsTrue si _ state = si state knowledgeAboutColor1 :: Knowledge knowledgeAboutColor1 = knowledgeAbout $ stateInfoColor 0 knowledgeAboutColor2 :: Knowledge knowledgeAboutColor2 = knowledgeAbout $ stateInfoColor 1 knowledgeAboutColor3 :: Knowledge knowledgeAboutColor3 = knowledgeAbout $ stateInfoColor 2 

The Knowledge type describes some “knowledge” about the world. As we will see, the Knowledge type will be combined with the StateInfo type in different ways. This is a very important type. I will dwell on it in more detail.



As can be seen from the definition of Knowledge , this is a function that, from the state of the world, computes some filtering function. Those. we transfer the "present" state of the world, and it gives out a certain subset of possible states that do not contradict our knowledge.



For example, the knowledgeAboutColor1 function is knowledge about the color of the first sage. If I give the state [White, Black, Black], in which the color of the first sage is white, then it will return a function that filters out all the states in which the first sage has a different color.



We will not have special structures denoting sage. We will reason in terms of "knowledge." Here is an example of such reasoning.



= + + ,



= +





Here are some more helper functions in terms of Knowledge and StateInfo .

 knowledgeAnd :: [Knowledge] -> Knowledge knowledgeAnd list stateTrue = \s -> and $ map (\f -> f stateTrue s) list stateInfoList :: [StateInfo a] -> StateInfo [a] stateInfoList sil state = map (\si-> si state) sil knowledgeImply :: Knowledge -> Knowledge -> StateInfo Bool knowledgeImply knowledge1 knowledge2 state = and $ map (\(b1, b2) -> not $ and [b1, not b2]) $ map (\s -> (knowledge1 state s, knowledge2 state s)) fullState 

The knowledgeAnd function simply combines knowledge into one.



The action of the stateInfoList function is obvious from its type.



The third function of knowledgeImply more interesting. It is a statement that the second knowledge is derived from the first knowledge.



Next comes the code directly related to the task.

 type KnowledgeList = [(Knowledge, Knowledge)] insightList :: KnowledgeList -> StateInfo [Bool] insightList knowledgeList = stateInfoList $ map knowledgeInsight knowledgeList knowledgeInsight :: (Knowledge, Knowledge) -> StateInfo Bool knowledgeInsight (currentKnowledge, targetKnowledge) = knowledgeImply currentKnowledge targetKnowledge manStart_1 = knowledgeAnd [knowledgeAboutColor2, knowledgeAboutColor3, knowledgeAbout stateInfoAnyWhite] manStart_2 = knowledgeAnd [knowledgeAboutColor1, knowledgeAboutColor3, knowledgeAbout stateInfoAnyWhite] manStart_3 = knowledgeAnd [knowledgeAboutColor1, knowledgeAboutColor2, knowledgeAbout stateInfoAnyWhite] knowledgeList_1 :: KnowledgeList knowledgeList_1 = [(manStart_1, knowledgeAboutColor1), (manStart_2, knowledgeAboutColor2), (manStart_3, knowledgeAboutColor3)] insightList_1 :: StateInfo [Bool] insightList_1 = insightList knowledgeList_1 

The KnowledgeList type is something like a list of sages. For each sage we have a pair of knowledge. The first element is his current knowledge. The second element is what he is trying to figure out, namely the color of his hat.



The knowledgeInsight function calculates whether a particular sage could determine his color. In other words, does the knowledge to which he aspires flow from the knowledge that he possesses. Our magical knowledgeImply function is used.



Variables manStart_1 , manStart_2 , manStart_3 - this is the initial knowledge of the relevant sages.



The variable knowledgeList_1 is a list of all the wise men on the first day (their knowledge).



The insightList_1 variable is the first day’s voting results.



Having the results of the voting, we can compile a new list of knowledge of the sages.

 addNewKnowledge :: Knowledge -> KnowledgeList -> KnowledgeList addNewKnowledge newKnowledge knowledgeList = flip map knowledgeList $ \(oldKnowledge, targetKnowledge) -> (knowledgeAnd [oldKnowledge, newKnowledge], targetKnowledge) knowledgeList_2 :: KnowledgeList knowledgeList_2 = addNewKnowledge (knowledgeAbout insightList_1) knowledgeList_1 insightList_2 :: StateInfo [Bool] insightList_2 = insightList knowledgeList_2 knowledgeList_3 :: KnowledgeList knowledgeList_3 = addNewKnowledge (knowledgeAbout insightList_2) knowledgeList_2 insightList_3 :: StateInfo [Bool] insightList_3 = insightList knowledgeList_3 

With the help of the addNewKnowledge function , we go over all the wise men and add new knowledge to them (the results of the previous day’s voting).



Repeating the procedure several times, we obtain the variables insightList_1 , insightList_2 and insightList_3 - the voting results for three days.



The final touch is to output the result for a particular initial state.

 startState = [White, White, White] main = do putStr $ "day 1 result: " ++ (show $ insightList_1 startState) ++ "\n" putStr $ "day 2 result: " ++ (show $ insightList_2 startState) ++ "\n" putStr $ "day 3 result: " ++ (show $ insightList_3 startState) ++ "\n" 

Result

To begin, consider the most difficult and interesting option, when all caps are white.

 startState = [White, White, White] {- result: day 1 result: [False,False,False] day 2 result: [False,False,False] day 3 result: [True,True,True] -}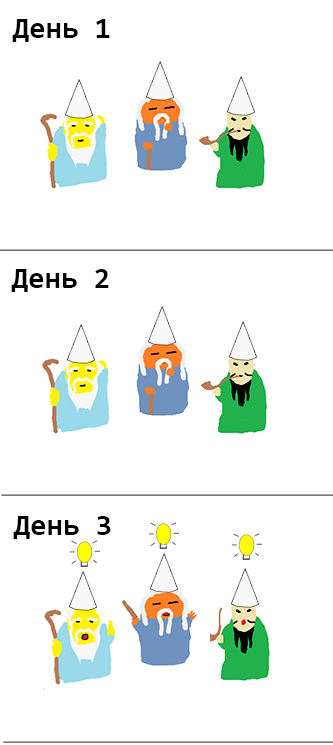 

In the first two days, the wise men thought. And on the third day, the three of them said they knew their color.



Unfortunately, it was not possible to identify the "most intelligent". We assume that all wise men are as smart as possible and use all available information to the fullest. In their reasoning, they all use the fact that other sages are also the most intelligent.



What happens if one of the caps is black?

 startState = [Black, White, White] {- result: day 1 result: [False,False,False] day 2 result: [False,True,True] day 3 result: [True,True,True] -}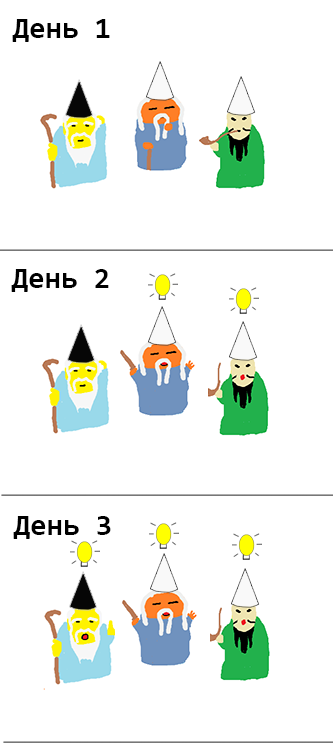 

We see that two wise men in white were able to determine their color on the second day. It is not surprising, because for them the whole situation boils down to the problem of two wise men. Looking at their reaction, the remaining sage was able to determine his color.



And here is an example with two black caps.

 startState = [Black, Black, White] {- result: day 1 result: [False,False,True] day 2 result: [True,True,True] day 3 result: [True,True,True] -} 

As you can see, the sage in a white cap on the first day was able to determine its color. And this is a clear signal to the rest of the wise men that they have black caps.

Conclusion

The resulting example is a good starting point for further research and experimentation. With it, you can solve other problems in the style of "I know that he knows that I know ..".



In my code, the number of wise men and days is tough. I did not specifically begin to generalize it to N sages and N days to make it clearer. Perhaps in the next article I will rewrite it through the komonad.