My remarks on the book by L.P. Plekhanov "Fundamentals of self-timed electronic circuits"
First of all, I want to say that over the 10 years that I have not been involved in asynchronous circuits, certain changes have occurred in this area. First of all, the change in terminology is striking. The term "asynchronous circuits" has taken over the term "self-timed circuits". It is this term that now refers to real asynchronous circuits, independent of the delays of logic elements. And the term "asynchronous circuits" got the designation of circuits that do not have this valuable quality, and, in general, all circuits without a clock signal. I decided to study in more detail what self-timed circuits are. The book indicated in the title seemed appropriate to me. Moreover, it is recommended as a textbook, and published not so long ago.

In the book, self-timed circuits are presented as a separate class of circuits with unique properties. But the definition of a self-timed circuit:
A self-timed circuit (CC scheme) is a circuit that has
two properties of error free operation:
')
This definition implies a hypothesis about Muller's delays. The second point is a consequence of the first. And the first point is nothing but the definition of the long-established term speed-independent (SI). That is, it turns out that self-timed circuits are not a separate class of circuits, but circuits synthesized by a certain method that is guaranteed by the SI property. Thus, “self-timed” is not a characteristic of the class of schemes, but a characteristic of the method of synthesis.
Let us consider in more detail the features of the self-timed synthesis method. I'll start with the way the scheme works. The self-timed method is adopted by the functional approach. This is justified by the fact that the event approach implies the mandatory closure of the circuit (simulation of the external environment). Hence the difficulty with the hierarchical description. I would call it ancient ridiculous prejudices. They appear to have been taken from the works of Warsaw 30 years ago. And without any understanding. The fact that Warsaw considered a simplified model, autonomous circuits, is understandable and quite reasonable. But it is impossible to raise intermediate results to the rank of dogma. In addition, the functional approach is secondary to the event approach. A functional description is nothing but the result of applying Muller’s method to an event description. Indeed, according to the change diagram, we obtain a truth table, and from it we calculate logical functions. As a result, we obtain a functional description. In fact, it turns out that the self-timed method is a superstructure over Muller's method. With the exception of combinational circuits, for which the functional description is quite natural. In addition, the functional description is defective in relation to the event. First, if the event description contains CSC contradictions, then a functional description cannot be compiled at all. Of course, the problem is easily solved by adding signals, but the self-timed method does not provide for this. Secondly, the event description is a description of the work of both the scheme itself and the external environment at the same time. The functional description describes the scheme only. A circuit without a description of the discipline of changes in input signals does not make sense. Indeed, the book is full of examples, but at best there is only a verbal description of the work of the external environment. In the end, the author is forced to introduce purely eventual concepts: the initiator and the continuator (for signals).
There is a paradoxical situation. Description of the scheme does not make sense without a description of the work of the external environment. But if the external environment makes a choice, then it is impossible to describe it functionally. We'll have to do it in an eventful way. But the event description of the external environment is also a description of the scheme itself. The external environment and the scheme are two mirror objects. It turns out that already having an event description of the scheme, we have to do its functional description.
Most likely, the choice of the functional approach is due to the peculiarities of the method itself, rather than the fact that this approach is preferable to the event approach. As a justification of the choice, it is argued that the functional description is more familiar to the developer. Timing charts are given as an example. But time diagrams, though clumsy, but still an event description. It explicitly presents the causal relationships between events (switching signals).
The next feature is paraphase signal coding. The thing is certainly redundant, but nothing can be done - this is the foundation of the method. The only solution for combinational circuits is a natural solution. In any case, for the synthesis of asynchronous combinational circuits, some analog of signal coding is necessary, for example, implemented as a choice. The same applies to the two-phase signal switching discipline, which is a consequence of signal coding.
Another consequence of coding is the indication of the inputs and outputs of logic elements. In fact, the display is not unusual. For example, in Muller’s model, the element outputs are displayed by themselves, just as the indicator indicates its own output. The inputs of the elements are indicated by the elements connected to these inputs. The novelty lies in the explicit use of the indicator. At the same time, you get such horrific things:

The problem, however, is solved with the help of a single-stage implementation of logical elements. But it is inappropriate to talk about a clean, uncompromising approach, which is stated at the beginning of the book.
All the above features are a means. Signal coding, indication, etc. they are internal properties of the method and do not add any new qualities to the schemes. And the result of applying these tools is the implementation of asynchronous circuits that are not dependent on the delays of the logic elements, in a monotonic basis. Yes, without a doubt, getting rid of input inverters of logic elements is important and necessary. Only the method proposed by Starodubtsev solves the same problem an order of magnitude easier and more efficient. Except, however, combinational circuits.
And now let us ask ourselves what problems does Muller's approach pose, how are these problems solved by the self-timed method and is it possible to solve these problems altogether? Obviously, there are two such problems: an unbounded basis for the implementation of logical elements and the exponential complexity of calculating logical functions.
I'll start with the last one. In the self-timed method, this problem is solved using hierarchical descriptions. That is the hope of chance. What if the complexity of the calculations is not very high. And what are the ways to solve this problem? First of all, these are alternative methods of calculation. As you know, logical functions are calculated from truth tables using Carnot maps, cubes, and the like. In general terms, of course, it is hardly possible to invent something new. But we are dealing with a specific task. Logical functions are computed for behaviors (schemas).
Here we must make a reservation that we are not talking about the functional descriptions of the behavior of the circuit, but only about the event. Yes, and only about those that operate with events, not states. For example STG. Indeed, the truth table is calculated from the data encrypted in the STG. But at the same time, when moving from STG to the truth table, very important information is lost, which makes it possible to significantly optimize the calculations. This is the data on which states are adjacent in the process of the circuit operation. Figuratively speaking, it is not necessary to explore the entire state space. It is enough to go through the path that is defined by the description of the scheme.
At one time, Starodubtsev, when he worked in the Warsaw group, proposed a similar algorithm. But the idea was hacked to the ground. Indeed, the algorithm was unsuccessful and inefficient, so to speak turned inside out. It was suggested that when building an implicant to expand the zone "1" (for the function I). Start with the minimum implicants (state) and gradually increase it by combining with neighboring states, as far as possible. In fact, it is necessary to expand the zone "0", that is, reduce the implicant until it fits into the desired area. Another advantage of this algorithm is that it allows you to completely abandon the concept of "state". The algorithm operates only with events and causal relationships between them.
But the algorithm itself does not eliminate the brute force. Therefore, we must use another direction to reduce the amount of computation: the calculation of logical functions of a previously known form. This requires a preliminary correction of behavior. This correction is carried out in 3 stages. First, multiple signals are eliminated, that is, signals whose switchings occur more than twice in the description. About this in more detail is written by me in the first article. Then the following situations are eliminated:
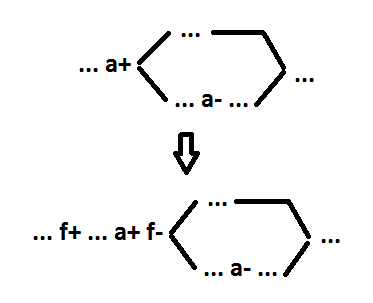
Finally, add each signal x to the dual signal y.

A pair of signals x and y are the simplest trigger. The excitation function of such a trigger is one implicant. Now the complexity of the calculation of the logical function becomes linear with respect to the number of events. The complexity of the preliminary correction is also linear.
And now we will return to the first problematic point of Muller’s method: unlimited basis for the implementation of logical elements. The self-timed method takes a step forward in this regard. The implementation basis is limited to logic elements without input inverters. But at the same time, the number of inputs of the element remains unlimited. Moreover, it is allowed to use elements with an unlimited number of logic levels (indicators). True, this problem is solved by a single-cascade implementation of logical elements. But in this case, the original thesis about the super-reliability of self-timed circuits sounds inappropriate. At the same time, there is a formal method of synthesis in a limited basis (2I-NO, 2I-NO).
Here I would like to dwell on the formal criteria for reliability of circuits and on ways to improve reliability. It's about the logical level. The delay wires accept a non-zero and finite, as in the logical elements. The cause of malfunctions in the work of the scheme are contests, interceptions, races, isochronous forks, Hazards ... All these are different names for the same phenomenon. Consider it in more detail. Take a logical element:
Talking about contests on a logical element makes no sense without specifying its behavior. For any logical element, you can lead the behavior in which the competition will be absent. Therefore, consider the following behavior:

The c- event is the direct cause of the a- event, although this causal relationship could be indirect. Why this is done, I will explain later. This behavior contains two interceptions (contests). First: between c- and a- events. Second: between events c + and b +. In general, for each logical element (in accordance with its behavior) an exhaustive list of interceptions can be made. Consider the first one in more detail. The interception is that in order to maintain at the output of a logic element x of value 1, it is necessary that the event c- be perceived on the OR element (component of the element x) earlier than the event a-.

In this case, the sequence of the events themselves is rigidly fixed. Event a- occurs after the event c-. That is, the proper functioning of the logic element depends on the propagation delays of the respective signals. For this interception, you can derive a formula for the element to work properly:
Where - wire delay from the output of the element c to the input of the element x,
- the delay of the NOT element, an integral part of the x element,
- the delay of the AND element, an integral part of the x element,
- wire delay from the output of the element c to the input of the element x,
- the delay element a,
- wire delay from the output of the element a to the input of the element x.
This ratio of delays is critical for the basis of NOT-AND-OR-NOT, that is, the probability of error is maximum. In general, it is possible to make up for the scheme a complete list of such ratios of delays, at which the scheme will work correctly.
How to increase the reliability of the scheme? To do this, reduce the left side of the critical delay ratio and increase the right side. The self-timed method takes the first step in this direction: a monotonic basis is used. The critical ratio of delays becomes (if we ignore the indicators):
Synthesis in the basis of AND-NOT, OR-NOT leads to this ratio of delays:
A special case of such a synthesis, synthesis in the basis of 2I-NOT, 2I-NO, I mentioned above. The next step is to increase the right side of the inequality. For this, it is necessary to increase the “length” of interception, that is, in our example, to space apart the events c- and a- further from each other. This can be done by inserting new signals between these events.
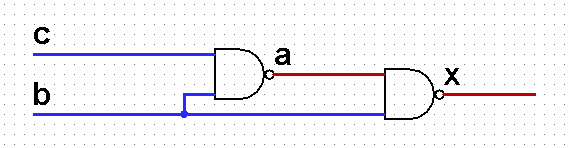
Consider as an example the scheme in the basis 2I-NOT, 2OR-NOT. Let schema element has a “short” interception (between events b- and a +). That is, event b- is the direct cause of event a +. A fragment of the scheme looks like this:
The behavior of this fragment is:
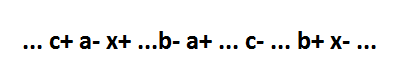
The consequences of the chosen implementation basis and the “short” interception on the x element are as follows: 1) the a element has the form 2I – NOT; 2) the signal c (the second input of element a) can be switched in a unique way (as shown in the figure above).
The task is to correct the scheme (by correcting the behavior) so that: 1) the scheme remains operable; 2) the basis of implementation remained the same; 3) no new elements with a “short” interception appeared; 4) interception on the element x would cease to be "short". The corrected behavior looks like this (added signals f, g, h):

The adjusted schema fragment now looks like this:

The adjustment affected only the signals x and a, only for the switching of these signals, the cause events were changed. Consequently, all other signals of the circuit have retained their logical functions. The interception length for the remaining signals of the circuit is at least not decreased. For the x element, interception is performed by f + and h- events, for a element - by c- and g + events, for f element - by g- and b + events, for g element - by f- and h + events, for h element - by b- and a + events . None of the interceptions are short. applying this procedure to all (if necessary) elements of the scheme, we obtain a scheme for which the worst delay ratio would be:
Where - wire delay,
- item delay.
Thus, by increasing the right-hand side of the inequality, the reliability of the circuit can be increased infinitely. The price for this is an increase in the scheme.
And a few more words about such a property as semi-modularity, widely used in the self-timed method. The property is generally useless, since it was introduced for autonomous circuits that have no practical value. But nevertheless, this property is thoughtlessly used, resulting in such meaningless actions as circuit closure, external environment simulation by some kind of circuit. What prevents to consider the external environment as a logical element that has several outputs? Its behavior is described. And how he realizes this behavior should not interest us at all.
Any choice behavior is by definition not semi-modular. Nevertheless, it is easy to synthesize a scheme for such behaviors that does not depend on element delays. To simulate in this case the external environment by some kind of scheme is not possible at all. The scheme itself cannot make a choice; it is made by the external environment.
In this property, of course, there is a rational grain: the prohibition of conflict situations (the removal of the excitation without switching the signal). But it should concern only the signals generated by the circuit (internal and output). In general, the problem of semimodularity (or rather, its analogue) should be solved not at the stage of analysis of the finished scheme, not at the stage of synthesis, not at the stage of drawing up the initial task. This problem should be solved by the wording of the description language. In this language, there is nothing difficult, this is a narrowing of the STG. A language must implement only two mechanisms: choice and causal relationships. The first allows conflicting situations regarding input signals. The second prohibits conflicts in relation to internal and output signals: if event-causes have occurred, then event-consequences must occur. Manipulations with behavior within the description language automatically guarantee no conflicts. Analysis of ready-made schemes that do not have a detailed description of their work is not a thankful business. This means that the scheme is made “on the knee”, at random, without a sufficiently elaborated methodology. Using such schemes is bad practice.
Summarizing, a reasonable area of application for the self-timed method is combinational circuits. Applying this method to questionable behavior. At least in the book, this topic is set aside by silence. The claimed unique properties of self-timed circuits are exaggerated. The self-timed method solves one not the most difficult task: implementation in a monotone basis. Method attributes (indication, signal coding, etc.) are only method attributes and do not carry any additional payload. True, one thing really struck me. This is a circuit for converting a unary signal into a SFC signal. I still believed that making such a scheme outside the event model is unlikely. However, the author did it.

In the book, self-timed circuits are presented as a separate class of circuits with unique properties. But the definition of a self-timed circuit:
A self-timed circuit (CC scheme) is a circuit that has
two properties of error free operation:
')
- no races for any finite element delays;
- failsafe.
This definition implies a hypothesis about Muller's delays. The second point is a consequence of the first. And the first point is nothing but the definition of the long-established term speed-independent (SI). That is, it turns out that self-timed circuits are not a separate class of circuits, but circuits synthesized by a certain method that is guaranteed by the SI property. Thus, “self-timed” is not a characteristic of the class of schemes, but a characteristic of the method of synthesis.
Let us consider in more detail the features of the self-timed synthesis method. I'll start with the way the scheme works. The self-timed method is adopted by the functional approach. This is justified by the fact that the event approach implies the mandatory closure of the circuit (simulation of the external environment). Hence the difficulty with the hierarchical description. I would call it ancient ridiculous prejudices. They appear to have been taken from the works of Warsaw 30 years ago. And without any understanding. The fact that Warsaw considered a simplified model, autonomous circuits, is understandable and quite reasonable. But it is impossible to raise intermediate results to the rank of dogma. In addition, the functional approach is secondary to the event approach. A functional description is nothing but the result of applying Muller’s method to an event description. Indeed, according to the change diagram, we obtain a truth table, and from it we calculate logical functions. As a result, we obtain a functional description. In fact, it turns out that the self-timed method is a superstructure over Muller's method. With the exception of combinational circuits, for which the functional description is quite natural. In addition, the functional description is defective in relation to the event. First, if the event description contains CSC contradictions, then a functional description cannot be compiled at all. Of course, the problem is easily solved by adding signals, but the self-timed method does not provide for this. Secondly, the event description is a description of the work of both the scheme itself and the external environment at the same time. The functional description describes the scheme only. A circuit without a description of the discipline of changes in input signals does not make sense. Indeed, the book is full of examples, but at best there is only a verbal description of the work of the external environment. In the end, the author is forced to introduce purely eventual concepts: the initiator and the continuator (for signals).
There is a paradoxical situation. Description of the scheme does not make sense without a description of the work of the external environment. But if the external environment makes a choice, then it is impossible to describe it functionally. We'll have to do it in an eventful way. But the event description of the external environment is also a description of the scheme itself. The external environment and the scheme are two mirror objects. It turns out that already having an event description of the scheme, we have to do its functional description.
Most likely, the choice of the functional approach is due to the peculiarities of the method itself, rather than the fact that this approach is preferable to the event approach. As a justification of the choice, it is argued that the functional description is more familiar to the developer. Timing charts are given as an example. But time diagrams, though clumsy, but still an event description. It explicitly presents the causal relationships between events (switching signals).
The next feature is paraphase signal coding. The thing is certainly redundant, but nothing can be done - this is the foundation of the method. The only solution for combinational circuits is a natural solution. In any case, for the synthesis of asynchronous combinational circuits, some analog of signal coding is necessary, for example, implemented as a choice. The same applies to the two-phase signal switching discipline, which is a consequence of signal coding.
Another consequence of coding is the indication of the inputs and outputs of logic elements. In fact, the display is not unusual. For example, in Muller’s model, the element outputs are displayed by themselves, just as the indicator indicates its own output. The inputs of the elements are indicated by the elements connected to these inputs. The novelty lies in the explicit use of the indicator. At the same time, you get such horrific things:

The problem, however, is solved with the help of a single-stage implementation of logical elements. But it is inappropriate to talk about a clean, uncompromising approach, which is stated at the beginning of the book.
All the above features are a means. Signal coding, indication, etc. they are internal properties of the method and do not add any new qualities to the schemes. And the result of applying these tools is the implementation of asynchronous circuits that are not dependent on the delays of the logic elements, in a monotonic basis. Yes, without a doubt, getting rid of input inverters of logic elements is important and necessary. Only the method proposed by Starodubtsev solves the same problem an order of magnitude easier and more efficient. Except, however, combinational circuits.
And now let us ask ourselves what problems does Muller's approach pose, how are these problems solved by the self-timed method and is it possible to solve these problems altogether? Obviously, there are two such problems: an unbounded basis for the implementation of logical elements and the exponential complexity of calculating logical functions.
I'll start with the last one. In the self-timed method, this problem is solved using hierarchical descriptions. That is the hope of chance. What if the complexity of the calculations is not very high. And what are the ways to solve this problem? First of all, these are alternative methods of calculation. As you know, logical functions are calculated from truth tables using Carnot maps, cubes, and the like. In general terms, of course, it is hardly possible to invent something new. But we are dealing with a specific task. Logical functions are computed for behaviors (schemas).
Here we must make a reservation that we are not talking about the functional descriptions of the behavior of the circuit, but only about the event. Yes, and only about those that operate with events, not states. For example STG. Indeed, the truth table is calculated from the data encrypted in the STG. But at the same time, when moving from STG to the truth table, very important information is lost, which makes it possible to significantly optimize the calculations. This is the data on which states are adjacent in the process of the circuit operation. Figuratively speaking, it is not necessary to explore the entire state space. It is enough to go through the path that is defined by the description of the scheme.
At one time, Starodubtsev, when he worked in the Warsaw group, proposed a similar algorithm. But the idea was hacked to the ground. Indeed, the algorithm was unsuccessful and inefficient, so to speak turned inside out. It was suggested that when building an implicant to expand the zone "1" (for the function I). Start with the minimum implicants (state) and gradually increase it by combining with neighboring states, as far as possible. In fact, it is necessary to expand the zone "0", that is, reduce the implicant until it fits into the desired area. Another advantage of this algorithm is that it allows you to completely abandon the concept of "state". The algorithm operates only with events and causal relationships between them.
But the algorithm itself does not eliminate the brute force. Therefore, we must use another direction to reduce the amount of computation: the calculation of logical functions of a previously known form. This requires a preliminary correction of behavior. This correction is carried out in 3 stages. First, multiple signals are eliminated, that is, signals whose switchings occur more than twice in the description. About this in more detail is written by me in the first article. Then the following situations are eliminated:

Finally, add each signal x to the dual signal y.

A pair of signals x and y are the simplest trigger. The excitation function of such a trigger is one implicant. Now the complexity of the calculation of the logical function becomes linear with respect to the number of events. The complexity of the preliminary correction is also linear.
And now we will return to the first problematic point of Muller’s method: unlimited basis for the implementation of logical elements. The self-timed method takes a step forward in this regard. The implementation basis is limited to logic elements without input inverters. But at the same time, the number of inputs of the element remains unlimited. Moreover, it is allowed to use elements with an unlimited number of logic levels (indicators). True, this problem is solved by a single-cascade implementation of logical elements. But in this case, the original thesis about the super-reliability of self-timed circuits sounds inappropriate. At the same time, there is a formal method of synthesis in a limited basis (2I-NO, 2I-NO).
Here I would like to dwell on the formal criteria for reliability of circuits and on ways to improve reliability. It's about the logical level. The delay wires accept a non-zero and finite, as in the logical elements. The cause of malfunctions in the work of the scheme are contests, interceptions, races, isochronous forks, Hazards ... All these are different names for the same phenomenon. Consider it in more detail. Take a logical element:
Talking about contests on a logical element makes no sense without specifying its behavior. For any logical element, you can lead the behavior in which the competition will be absent. Therefore, consider the following behavior:

The c- event is the direct cause of the a- event, although this causal relationship could be indirect. Why this is done, I will explain later. This behavior contains two interceptions (contests). First: between c- and a- events. Second: between events c + and b +. In general, for each logical element (in accordance with its behavior) an exhaustive list of interceptions can be made. Consider the first one in more detail. The interception is that in order to maintain at the output of a logic element x of value 1, it is necessary that the event c- be perceived on the OR element (component of the element x) earlier than the event a-.

In this case, the sequence of the events themselves is rigidly fixed. Event a- occurs after the event c-. That is, the proper functioning of the logic element depends on the propagation delays of the respective signals. For this interception, you can derive a formula for the element to work properly:
Where - wire delay from the output of the element c to the input of the element x,
- the delay of the NOT element, an integral part of the x element,
- the delay of the AND element, an integral part of the x element,
- wire delay from the output of the element c to the input of the element x,
- the delay element a,
- wire delay from the output of the element a to the input of the element x.
This ratio of delays is critical for the basis of NOT-AND-OR-NOT, that is, the probability of error is maximum. In general, it is possible to make up for the scheme a complete list of such ratios of delays, at which the scheme will work correctly.
How to increase the reliability of the scheme? To do this, reduce the left side of the critical delay ratio and increase the right side. The self-timed method takes the first step in this direction: a monotonic basis is used. The critical ratio of delays becomes (if we ignore the indicators):
Synthesis in the basis of AND-NOT, OR-NOT leads to this ratio of delays:
A special case of such a synthesis, synthesis in the basis of 2I-NOT, 2I-NO, I mentioned above. The next step is to increase the right side of the inequality. For this, it is necessary to increase the “length” of interception, that is, in our example, to space apart the events c- and a- further from each other. This can be done by inserting new signals between these events.
Consider as an example the scheme in the basis 2I-NOT, 2OR-NOT. Let schema element has a “short” interception (between events b- and a +). That is, event b- is the direct cause of event a +. A fragment of the scheme looks like this:

The behavior of this fragment is:
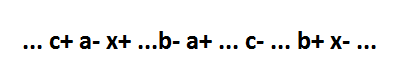
The consequences of the chosen implementation basis and the “short” interception on the x element are as follows: 1) the a element has the form 2I – NOT; 2) the signal c (the second input of element a) can be switched in a unique way (as shown in the figure above).
The task is to correct the scheme (by correcting the behavior) so that: 1) the scheme remains operable; 2) the basis of implementation remained the same; 3) no new elements with a “short” interception appeared; 4) interception on the element x would cease to be "short". The corrected behavior looks like this (added signals f, g, h):

The adjusted schema fragment now looks like this:

The adjustment affected only the signals x and a, only for the switching of these signals, the cause events were changed. Consequently, all other signals of the circuit have retained their logical functions. The interception length for the remaining signals of the circuit is at least not decreased. For the x element, interception is performed by f + and h- events, for a element - by c- and g + events, for f element - by g- and b + events, for g element - by f- and h + events, for h element - by b- and a + events . None of the interceptions are short. applying this procedure to all (if necessary) elements of the scheme, we obtain a scheme for which the worst delay ratio would be:
Where - wire delay,
- item delay.
Thus, by increasing the right-hand side of the inequality, the reliability of the circuit can be increased infinitely. The price for this is an increase in the scheme.
And a few more words about such a property as semi-modularity, widely used in the self-timed method. The property is generally useless, since it was introduced for autonomous circuits that have no practical value. But nevertheless, this property is thoughtlessly used, resulting in such meaningless actions as circuit closure, external environment simulation by some kind of circuit. What prevents to consider the external environment as a logical element that has several outputs? Its behavior is described. And how he realizes this behavior should not interest us at all.
Any choice behavior is by definition not semi-modular. Nevertheless, it is easy to synthesize a scheme for such behaviors that does not depend on element delays. To simulate in this case the external environment by some kind of scheme is not possible at all. The scheme itself cannot make a choice; it is made by the external environment.
In this property, of course, there is a rational grain: the prohibition of conflict situations (the removal of the excitation without switching the signal). But it should concern only the signals generated by the circuit (internal and output). In general, the problem of semimodularity (or rather, its analogue) should be solved not at the stage of analysis of the finished scheme, not at the stage of synthesis, not at the stage of drawing up the initial task. This problem should be solved by the wording of the description language. In this language, there is nothing difficult, this is a narrowing of the STG. A language must implement only two mechanisms: choice and causal relationships. The first allows conflicting situations regarding input signals. The second prohibits conflicts in relation to internal and output signals: if event-causes have occurred, then event-consequences must occur. Manipulations with behavior within the description language automatically guarantee no conflicts. Analysis of ready-made schemes that do not have a detailed description of their work is not a thankful business. This means that the scheme is made “on the knee”, at random, without a sufficiently elaborated methodology. Using such schemes is bad practice.
Summarizing, a reasonable area of application for the self-timed method is combinational circuits. Applying this method to questionable behavior. At least in the book, this topic is set aside by silence. The claimed unique properties of self-timed circuits are exaggerated. The self-timed method solves one not the most difficult task: implementation in a monotone basis. Method attributes (indication, signal coding, etc.) are only method attributes and do not carry any additional payload. True, one thing really struck me. This is a circuit for converting a unary signal into a SFC signal. I still believed that making such a scheme outside the event model is unlikely. However, the author did it.
Source: https://habr.com/ru/post/349238/
All Articles