Modeling Dynamic Systems: An Introduction to GNU Octave
Once upon a time there were smart, but very greedy people who wrote a wonderful Matlab program. They were smart because the program came out good, and greedy, because they loved money very much. So they loved that they took them for their Matlab not only from serious uncles, they earn money from poor students, but also from poor students, who sometimes didn’t even buy a dry crust of bread for anything. And the tale would end soon and sadly if the world was not without good and intelligent people who wrote programs similar to matlab, at least working for a while, but free for everyone. And open source. So the poor students themselves began to write those programs, and they began to work better and better every year. And then all began to live, be well, but good to make ...
Introduction
Most scientific workers do not puzzle over how numerical methods are arranged inside. They simply use them, applying specialized packages of numerical calculations in their work. This does not mean that you do not need to understand how these methods are organized. The program is written by a person, and it is erroneous for him. And errors appear even in the most expensive and sophisticated systems of numerical mathematics very often. In addition, there are tasks where the use of standard systems is impossible.
At the same time, the ability to use universal mathematical software is a must have for a modern scientist, because by inventing a bicycle you can never get to the solution of your main task. Today we will look at the promised Octave, trying to solve with it the next children's task, making non-children's conclusions.
1. What is Octave and where to get it
GNU Octave is a free math package of numerical mathematics based on the concepts of its proprietary colleague Matlab. It is available for all popular desktop platforms today, and you can get it by going to the download section on the official website.
')
Most of the screen is occupied by the so-called command window, with an invite of the command line of the form ">>". Enter there and press Enter.
>> 2 + 2 ans = 4 smartly, the ans variable contains the result of the last operation, unless you explicitly set the variable for the result, for example
>> x = 3 + 2 x = 5 variables are introduced “on the fly”, as is customary in interpreted languages. Yes, the m-language octave itself is an interpreter language, very similar to the matlab language. Once set, the variable retains its value and type until the next assignment, or until the command shell memory is completely cleared.
>> x + ans ans = 9 On the left side of the window there is an area in which are located (from top to bottom): a file manager, a list of global variables with their values, as well as a history of entered commands.
It is worth paying attention to the fact that for variables the dimension (Dimention) 1x1 is indicated. The main data type in Octave, as in Matlab is the matrix. So our numbers are actually 1 by 1 matrixes.
You can clear all global variables by selecting Edit -> Clear Workspace from the menu, and clear the command window by right-clicking on it and choosing Clear Window. Perform the cleaning of variables and entering x we get
>> x error: 'x' undefined near line 1 column 1 >> x = 3 x = 3 >> x x = 3 it can be seen that the variable x became unavailable until we explicitly assigned it a value again.
Frankly speaking, I have never worked with Ocatve and understand with the reader. Therefore, suppose that we already know enough to solve any problem. For example, the one that was solved last time . But first…
2. Normal form of Cauchy
Remember, I said that the majority, with the exception of a certain narrow class, of numerical methods are “sharpened” for equations of the 1st order? And what, before applying these methods to solving an equation, does one have to lower its order? The trouble is that not all equations can be reduced in order. However, any equation of the nth order can be turned into n equations of the 1st order. This is called converting the equation to the normal form of Cauchy . Take the past equation
Remember that
then
and we obtain instead of one equation of the 2nd order two equations of the 1st order, which need to be solved together, simultaneously
This is not just one equation, but a system of differential equations containing two unknown dependencies and .
How to solve a system of equations numerically? Yes, just like one equation. Let's collect all our variables in a column vector (or an array, or a column matrix, as it is convenient for whom it is not important to express it)
and the right parts also collect in the column vector
Then the Euler recurrence formula will be valid for each element of these columns.
where n is the number of equations, in our case there are two.
Why am I doing all this? And the fact that Octave requires that differential equations be represented in Cauchy’s normal form.
From the point of view of mechanics, the column vector y is called the state vector of the system or the vector of phase coordinates . Then our system of equations turns into a single vector equation
Now take, and in the Octave command window, type
>> function dydt = F(y, t) Thus, we define a function that accepts the current value of the phase coordinates y and the current time t at the input, and returns the value of the derivatives of the phase coordinates at the output. We see that the command line prompt ">>" is gone, the system is waiting for us to finish inputting the function body with the endfunction keyword. Continue to dial the function
>> function dydt = F(y, t) g = 10 dydt(1) = y(2) dydt(2) = -g endfunction So, in the body of the function, we determined g = 10 - the value of gravitational acceleration we have adopted. We see what did not appear in the list of variables on the left — this variable is local, and exists only within a function. The variable y is a matrix-column, the first element of which y (1) is the coordinate z, the second element y (2) is the projection of the velocity vector v z . Accordingly, dydt is the value that our function returns, it is also a column matrix whose first element is the time derivative of z, and the second is the time derivative of v z . That is, we wrote down our system of differential equations in terms of Octave.
Now we define the range of time for which we need to get the result. Let it be ten points from 0 to 1 second, in increments of 0.1 - compare the result with the manual example
>> t0 = 0 t0 = 0 >> tend = 1 tend = 1 >> deltaT = 0.1 deltaT = 0.10000 >> t = [t0:deltaT:tend] t = 0.00000 0.10000 0.20000 0.30000 0.40000 0.50000 0.60000 0.70000 0.80000 0.90000 1.00000 Everything is obvious here: t0 is the initial moment of time, tend is the final moment of time. But deltaT = 0.1 second is not an integration step ! This is the interval at which Ocatve will display for us a numerical solution of the equation. The last command forms an array of points in time for which we want to get a solution.
As you know from the previous article , to solve the equation, it is necessary to know the initial values of the velocity and coordinates numerically. You must set them for Octave
>> y0 = [100; 0] y0 = 100 0 thus, we determined the matrix-column containing the initial coordinate and the initial value of the vertical projection of velocity. Now solve the equation
>> y = lsode("F", y0, t) The lsode function solves the equation for us numerically. The first parameter is the name of the function that calculates the derivatives of the phase coordinates. This is a function F, we set it. The second parameter is the initial conditions , that is, the values of the phase coordinates at time t = t0. The last parameter is an array of time points for which we want to calculate phase coordinate values. Click Enter ...
In response, a mountain of tripe falls out, ending with a sentence
g = 10 dydt = -0.99690 dydt = -0.99690 -10.00000 g = 10 dydt = -0.99690 dydt = -0.99690 -10.00000 g = 10 dydt = -0.99690 dydt = -0.99690 -10.00000 g = 10 dydt = -1.9936 -- less -- (f)orward, (b)ack, (q)uit we are offered to flip the tripe further (f), go back (b), or quit (q). Those who know * nix-like systems know that this is a console output running under the unix utility less. We pretend we don’t know, we’ll get out of here by pressing q on the keyboard.
Now type in the command line "y" and press Enter
>> y y = 100.00000 0.00000 99.95000 -1.00000 99.80000 -2.00000 99.55000 -3.00000 99.20000 -4.00000 98.75000 -5.00000 98.20000 -6.00000 97.55000 -7.00000 96.80000 -8.00000 95.95000 -9.00000 95.00000 -10.00000 Nothing like? Well, of course, this is the very solution we received for the problem from the previous article. Only now it is surprisingly accurate - the values coincide with the analytical solution! Let me tell you a secret - this is the exact solution to our problem. This is due to the fact that the lsode function does not use the Euler method for solving the problem, but something more advanced. The movement of the stone occurs with constant acceleration, and the formula of numerical approximation, which is used in this method, obviously just coincides with the analytical solution of the problem. Although, if you crawl into the wilds of a floating-point representation of the machine, then ... Well, okay, now this is not about that.
3. We build the schedule
Type the command now
>> plot(t, y) A pop-up window with a graphical representation of the solution.
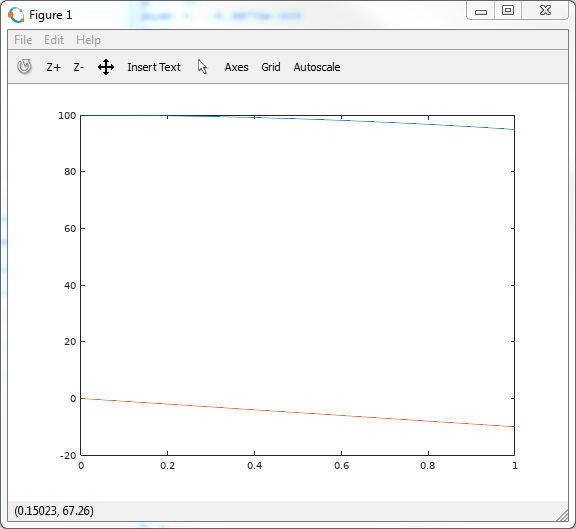
The blue curve above is the coordinate of the stone. Orange below is the vertical projection of speed. The entered command is inconvenient because it builds a schedule for all functions at once. And if we want to build, the dependence of speed on height? Then do this
>> plot(y(:,1), y(:,2)) A graph will be constructed, where the variable y (1) will go along the abscissa axis, and y (2) along the ordinate axis, which is respectively the height and the vertical projection of velocity
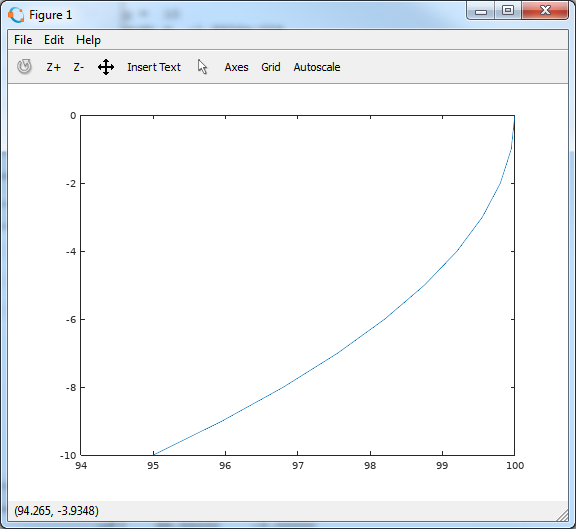
Such a graph in mechanics is called the phase portrait of the system , that is, the trajectory of the system in the space of phase coordinates. In this case, the phase coordinates are the height of the stone above the surface of the Earth and its speed. In mechanics, it is often impossible to obtain an exact solution in the form of functions of time, but one can relate coordinates and velocities to each other on the basis of energy considerations. According to the obtained dependences, you can find the phase trajectory of the system and make many conclusions about the nature of its movement without solving the problem to the end. We will talk about this too sometime.
In the meantime, I propose to perform an independent task - build a graph of the dependence of height on time and speed on time in separate windows. And try not to look under the spoiler
Answer
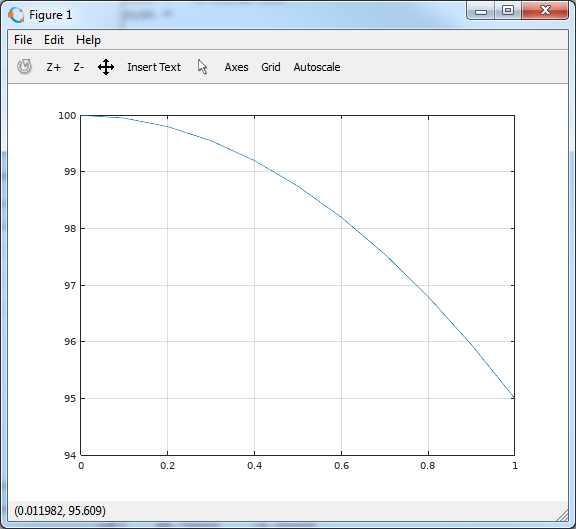
Height z (t)
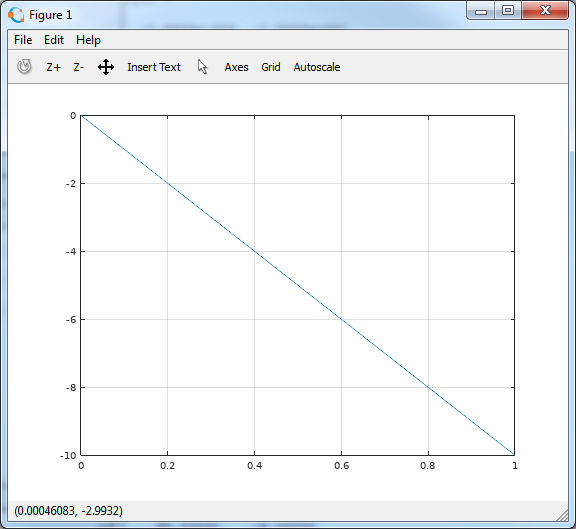
Speed v z (t)
>> plot(t, y(:,1)) 
Speed v z (t)
>> plot(t, y(:,2)) 
Conclusion
On this, the first acquaintance with Octave, as a medium for numerical modeling, will be considered finished. Now we have a powerful tool by which we will comprehend more sophisticated wisdom.
Thank you for your attention, see you!
Source: https://habr.com/ru/post/349204/
All Articles