Regular expressions: no magic

The code for this post, like the post itself, is laid out on github .



Until recently, regular expressions seemed like magic to me. I could not understand how it can be determined whether the string matches the specified regular expression. And now I understand it! Below is the implementation of a simple regular expression engine in less than 200 lines of code.

Part 1: Parsing

Specification

Implementing regular expressions completely is quite a challenge; worse, it will teach you little. The version we are implementing is enough to study the topic without slipping into a routine. Our regular expression language will support the following:

')

• . - match any character
• | - match abc or cde
• + - match one or more previous patterns
• * - match 0 or more of the previous pattern
• ( and ) - for grouping

Although the set of options is small, it can be used to create interesting regexes, for example, m (t|n| ) | b m (t|n| ) | b allows you to find subtitles for Star Wars without subtitles for Star Trek, or (..)* to find the set of all lines of even length.

Attack plan

We will analyze regular expressions in three steps:

1. Parsing (parsing) a regular expression into a syntax tree
2. Convert the syntax tree to the state machine
3. Analysis of the state machine for our row

For the analysis of regular expressions (more on this below) we will use a state machine called NFA . At a high level, the NFA will represent our regex. Upon receipt of the input data, we will move to NFA from state to state. If we come to a point from which it is impossible to make a valid transition, then the regular expression does not match the string.



This approach was first demonstrated by one of the Unix authors Ken Thompson. In his 1968 article in CACM magazine, he outlined the principles for implementing a text editor and added this approach as an interpreter of regular expressions. The only difference is that his article was written in machine code 7094. At that time, everything was much more hardcore.



This algorithm is a simplification of how engines without reverse lookup, like RE2, analyze regular expressions in provable linear time. It is very different from the regex engines from Python and Java, which use reverse lookup. For given input data with small lines, they run almost infinitely. Our implementation will be done in O(length(input) * length(expression) .



My approach roughly corresponds to the strategy laid out by Russ Cox in his amazing post .

Regular Expression Representation

Let's step back and think about how to represent a regular expression. Before we start analyzing a regular expression, we need to convert it into a data structure with which the computer can work. Although strings have a linear structure, regular expressions have a natural hierarchy.



Let's look at the string abc|(c|(de)) . If we left it with a string, we would have to go back and perform transitions, tracking different sets of brackets when analyzing an expression. One solution is to convert it to a tree that a computer can easily bypass. For example, b+a turns into the following: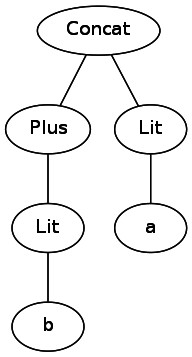





To represent the tree, we need to create a class hierarchy. For example, our class Or must have two subtrees representing both of its sides. From the specification it is clear that we need to recognize four different components of regular expressions: + , * , | and character literals like . , a and b . In addition, we also need to represent cases where one expression follows another. Here are our classes:

 abstract class RegexExpr // ., a, b case class Literal(c: Char) extends RegexExpr // a|b case class Or(expr1: RegexExpr, expr2: RegexExpr) extends RegexExpr // ab -> Concat(a,b); abc -> Concat(a, Concat(b, c)) case class Concat(first: RegexExpr, second: RegexExpr) extends RegexExpr // a* case class Repeat(expr: RegexExpr) extends RegexExpr // a+ case class Plus(expr: RegexExpr) extends RegexExpr 

Regular expression parsing

To move from string to tree view, we need to use a conversion process known as " parsing (parsing) ". I will not talk in detail about building parsers. Instead, I will lay out information that is enough to point you in the right direction if you decide to write your own. I will briefly talk about how to parse regular expressions using parser combinator library Scala.



The Scala parser library allows us to write a parser by simply writing a set of rules describing our language . Unfortunately, it uses a lot of stupid characters, but I hope you can get through the noise and get a general understanding of what is happening.



When implementing a parser, we need to determine the order of operations. Just as in arithmetic, PEMDAS is used [approx. per. P arentheses, E xponents, M ultiplication / D ivision, A ddition / S ubtraction - a mnemonic that allows you to remember the order in which arithmetic operations are performed] and a regular set of rules is used in regular expressions. We can express it more formally with the help of the idea of ​​“binding” the operator to the symbol next to it. Different operators “become attached” with different strengths — by analogy, in expressions like 5 + 6 * 4, the operator * binds more strongly than + . In regular expressions, * binds more strongly than | . One could imagine this in the form of a tree in which the weakest operators are at the top.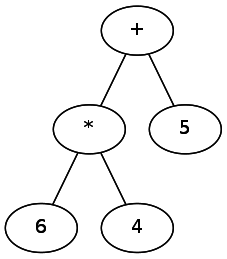





Therefore, we must first parse the weaker operators, and behind them the already stronger operators. When parsing, this can be represented as extracting the operator, adding it to the tree, and then recursively processing the remaining two parts of the string.



In regular expressions, the binding strength is as follows:

1. Character literals and parentheses
2. + and *
3. "Concatenation" - a follows b
4. |

Since we have four levels of binding power, we need four different types of expressions. We called them (arbitrarily enough): lit , lowExpr ( + , * ), midExpr (concatenation) and highExpr ( | ). Let's go to the code. First, we will create a parser for the most basic level, for a single character:

 object RegexParser extends RegexParsers { def charLit: Parser[RegexExpr] = ("""\w""".r | ".") ^^ { char => Literal(char.head) } 

Let's take a minute to explain the syntax. The code defines a parser that RegexExpr . The right side says: “Find something that matches \w (to any word symbol) or point. If found, turn it into a Literal . ”



The brackets must be defined at the lowest level of the parser, because they have the strongest reference. However, we need to be able to put something in brackets. We can achieve this with the following code:

  def parenExpr: Parser[RegexExpr] = "(" ~> highExpr <~ ")" def lit: Parser[RegexExpr] = charLit | parenExpr 

Here we define * and + :

  def repeat: Parser[RegexExpr] = lit <~ "*" ^^ { case l => Repeat(l) } def plus: Parser[RegexExpr] = lit <~ "+" ^^ { case p => Plus(p) } def lowExpr: Parser[RegexExpr] = repeat | plus | lit 

Next, we define the next level - concatenation:

  def concat: Parser[RegexExpr] = rep(lowExpr) ^^ { case list => listToConcat(list)} def midExpr: Parser[RegexExpr] = concat | lowExpr 

Finally, we define "or":

  def or: Parser[RegexExpr] = midExpr ~ "|" ~ midExpr ^^ { case l ~ "|" ~ r => Or(l, r)} 

And at the end we define highExpr . highExpr is or , the weakest binding operator, or, if not, then midExpr .

  def highExpr: Parser[RegexExpr] = or | midExpr 

Next, add some helper code to finish:

  def listToConcat(list: List[RegexExpr]): RegexExpr = list match { case head :: Nil => head case head :: rest => Concat(head, listToConcat(rest)) } def apply(input: String): Option[RegexExpr] = { parseAll(highExpr, input) match { case Success(result, _) => Some(result) case failure : NoSuccess => None } } } 

And that is all! If you take this code in Scala, you can generate syntax trees for any regular expression that meets the specification. The resulting data structures will be trees.



Now that we can transform our regular expressions into syntax trees, we are approaching to analyze them.

Part 2: Generating NFA

Convert the syntax tree to NFA

In the previous section, we converted the representation of a regular expression in the form of a flat string to the form of a hierarchical syntactic tree. In this part, we convert the syntax tree to a state machine. The finite automata leads the regex components into a linear graph form, creating the relations “a follows b follows c”. Representation in the form of a graph will simplify the analysis relative to the potential line.



Why do another conversion just to map to regex?



Of course, one could perform the conversion directly from the string to the state machine. You can even try to analyze a regular expression directly from the syntax tree or from a string. However, this will have to deal with much more complex code. Slowly lowering the level of abstraction, we can ensure that the code is easy to understand at every stage. This is especially important when building something like an interpreter of regular expressions with almost infinite boundary cases.

NFA, DFA and you

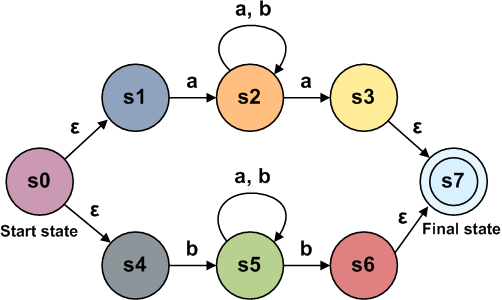
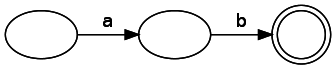
We will create a state machine called the NFA, or nondeterministic finite automata . It has two types of components: states and transitions. When presented on the state diagram are indicated by circles, and transitions - by arrows. The coincidence state is indicated by a double circle. If the transition is marked, this means that we must receive this character at the input in order to make this transition. Transitions may also not have tags. This means that we can make the transition without consuming the input data. Note: in the literature it is sometimes referred to as ε. A state machine representing a simple regex "ab":





Our nodes can have several valid subsequent states for the given input data, since the diagram below shows two paths that, when moving from a node, consume the same input data:





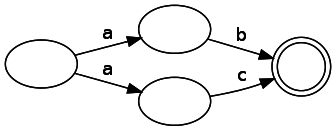
Contrast this with the deterministic state machine (DFA), in which, as its name implies, the given input data can lead to a single state change. On the one hand, this reduction in restrictions makes analysis a little more difficult, but on the other hand, as we will soon see, it greatly simplifies generating them from wood. From a fundamental point of view, NFA and DFA are similar to each other in the state machines that they can represent.

Transformation in theory

Let's outline the strategy for converting a syntax tree to NFA. Although it may seem intimidating, you will see that by breaking the process down into composable fragments, we will make it easy to understand. Recall the syntax elements that we need to convert:

1. Character literals: Lit(c: Char)
2. * : Repeat(r: RegexExpr)
3. + : Plus(r: RegexExpr)
4. Concatenation: Concat(: RegexExpr, : RegexExpr)
5. | : Or(a: RegexExpr, b: RegexExpr)

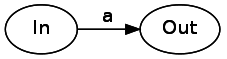
Subsequent changes were originally outlined by Thompson in his 1968 article. In the conversion schemes, In will refer to the state machine's entry point, and Out to the output one. In practice, they can be the “Match” state, the “Start” state, or other regex components. The In / Out abstraction allows us to link and combine finite state machines — the most important conclusion. We will apply this principle in a more general sense to transform from each element of the syntactic tree into a composable state machine.



Let's start with character literals. A character literal is a transition from one state to another that consumes input data. Consumption of the literal "a" will be as follows:





Next, let's explore concatenation. To concatenate the two components of the syntax tree, we just need to connect them with an arrow without labels. It is worth noting that in this example, as Concat may contain the concatenation of two arbitrary regular expressions, so A with B in the scheme can be finite automata, and not just separate states. Something a bit strange happens if both A and B are both literals. How do we connect two arrows without intermediate states? The answer is that literals can have phantom states on both sides in order to preserve the integrity of the state machine. Concat(A, B) converted to the following:





To represent Or(A, B) , we need to branch from the initial state to two separate states. After the completion of these automata, they both should indicate the following state ( Out ):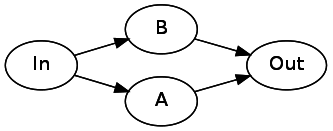





Let's look at * . An asterisk can be 0 or more repetitions of the pattern. To realize this, we need one connection to point directly to the next state, and one to go back to the current state through A A* will look like this: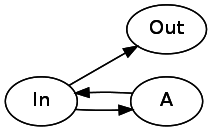





For + we will use a little trick. a+ is just aa* . In sum, Plus(A) can be rewritten as Concat(A, Repeat(A)) . We will do so, instead of developing a special pattern for this case. I had a special reason for including in language + : I wanted to show how other, more complex elements of regular expressions that I missed can often be expressed in categories of our language.

Conversion in practice

Now that we have a theoretical plan, let's see how to implement it in code. We will create a mutable graph to hold our tree. Although I prefer immutability, creating immutable graphs is annoying in its complexity, but I'm lazy.



If we try to reduce the above schemes to basic components, then we end up with three types of components: arrows that consume input data, a state of coincidence, and one state that splits into two states. I know it looks a little weird, and potentially unfinished. You just have to trust me that such a solution will lead to the purest code. Here are our three classes of NFA components:

 abstract class State class Consume(val c: Char, val out: State) extends State class Split(val out1: State, val out2: State) extends State case class Match() extends State 

Note: I made the Match case- instead of the regular class. Case classes in Scala give the class a convenient default characteristics. I used it because it gives equivalence based on values. This makes all Match objects equivalent — a useful property. For other types of NFA components, we need link equivalency.



Our code will recursively bypass the syntax tree, saving the andThen object as a parameter. andThen is what we will attach to the free exits of our expression. It is required because in an arbitrary branch of the syntactic tree there is not enough context for what will go on - andThen allows us to transfer this context down during a recursive walk. It also provides us with an easy way to add a Match state.



When it comes to handling Repeat , we have a problem. andThen for Repeat itself is a splitting operator. To deal with this problem, we introduce a placeholder, which will allow you to bind it later. We will present the placeholder as follows:

 class Placeholder(var pointingTo: State) extends State 

var in Placeholder means that pointingTo changeable. This is an isolated part of the variability, allowing us to conveniently create a cyclic graph. All other members are unchanged.



To begin with, andThen is Match() . This means that we will create a state machine corresponding to our Regex, which can then go to the Match state without consuming incoming data. The code will be short, but saturated:

  object NFA { def regexToNFA(regex: RegexExpr): State = regexToNFA(regex, Match()) private def regexToNFA(regex: RegexExpr, andThen: State): State = { regex match { case Literal(c) => new Consume(c, andThen) case Concat(first, second) => { //  first  NFA.  "" //    second  NFA. regexToNFA(first, regexToNFA(second, andThen)) } case Or(l, r) => new Split( regexToNFA(l, andThen), regexToNFA(r, andThen) ) case Repeat(r) => val placeholder = new Placeholder(null) val split = new Split( //     , //   -   r regexToNFA(r, placeholder), andThen ) placeholder.pointingTo = split placeholder case Plus(r) => regexToNFA(Concat(r, Repeat(r)), andThen) } } } 

And that is all! The ratio of sentences to lines of code in this part is quite high - each line encodes a lot of information, but it all comes down to the transformations discussed in the previous part. It should be explained - I did not just sit down and wrote the code in this form; the brevity and functionality of the code are the result of several iterations of working with data structures and an algorithm. Clean code is hard to write.



During the debugging process, I wrote a short script to generate dot files from NFA, so that you can see the generated NFA for debugging purposes. It is worth noting that the NFA generated by this code contains many unnecessary transitions and states. When writing an article, I tried to make the code as simple as possible, even at the cost of performance. Here are some examples of simple regular expressions: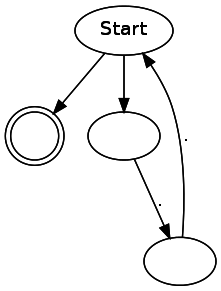



(..)*





ab





a|b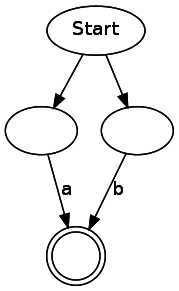





Now that we have NFA (the hardest part), we just have to analyze it (the part is easier).

Part 3: NFA Analysis

NFA, DFA and regular expressions

In the second part, we said that there are two types of finite automata: deterministic and non-deterministic. They have one key difference: a non-deterministic finite-state machine can have several paths to a single node for a single token; in addition, paths can be followed without receiving input data. In terms of expressive capabilities (often called “power”), NFA, DFA, and regular expressions are similar. This means that if you can express a rule or pattern (for example, strings of even length) with NFA, you can also express it through DFA or a regular expression. Let's first look at the regular expression abc* , expressed as DFA: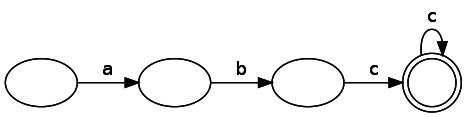





DFA analysis is straightforward - we simply move from state to state, consuming a line of input data. If we finish consuming the input data in a match state, then we have a match, otherwise it does not.On the other hand, our state machine is NFA. Generated by our NFA code for this regular expression looks like this:





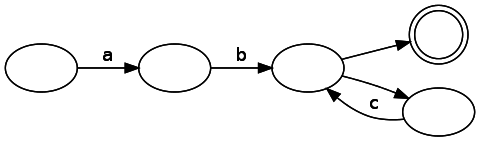
Notice that there are several unlabeled edges that can be walked without consuming a symbol. How to track them effectively? The answer is surprisingly simple: instead of tracking only one possible state, you need to keep a list of states in which the engine is currently located. When a branching occurs, one should follow both ways (turning one state into two). If the state has no valid transition for the current input, then it is removed from the list.



Here you need to consider two fine points: avoidance in the graph of infinite cycles and correct processing of transitions without input data. When analyzing a given state, we first go to all states to list all possible states reachable from our current state, if we do not consume more input data. At this stage, you need to be careful and keep "many visited" to avoid endless looping in the graph. Having listed all these states, we consume the next token of input data, either moving to these states or removing them from the list.

  object NFAEvaluator { def evaluate(nfa: State, input: String): Boolean = evaluate(Set(nfa), input) def evaluate(nfas: Set[State], input: String): Boolean = { input match { case "" => evaluateStates(nfas, None).exists(_ == Match()) case string => evaluate( evaluateStates(nfas, input.headOption), string.tail ) } } def evaluateStates(nfas: Set[State], input: Option[Char]): Set[State] = { val visitedStates = mutable.Set[State]() nfas.flatMap { state => evaluateState(state, input, visitedStates) } } def evaluateState(currentState: State, input: Option[Char], visitedStates: mutable.Set[State]): Set[State] = { if (visitedStates contains currentState) { Set() } else { visitedStates.add(currentState) currentState match { case placeholder: Placeholder => evaluateState( placeholder.pointingTo, input, visitedStates ) case consume: Consume => if (Some(consume.c) == input || consume.c == '.') { Set(consume.out) } else { Set() } case s: Split => evaluateState(s.out1, input, visitedStates) ++ evaluateState(s.out2, input, visitedStates) case m: Match => if (input.isDefined) Set() else Set(Match()) } } } } 

And that is all!

Finish the case

We are done with all the important code, but the API is not as clean as we would like. Now we need to create a single call user interface to call our regular expression engine. We will also add the ability to match the pattern anywhere in the line with a share of syntactic sugar.

  object Regex { def fullMatch(input: String, pattern: String) = { val parsed = RegexParser(pattern).getOrElse( throw new RuntimeException("Failed to parse regex") ) val nfa = NFA.regexToNFA(parsed) NFAEvaluator.evaluate(nfa, input) } def matchAnywhere(input: String, pattern: String) = fullMatch(input, ".*" + pattern + ".*") } 

And this is how the code is used:

  Regex.fullMatch("aaaaab", "a*b") // True Regex.fullMatch("aaaabc", "a*b") // False Regex.matchAnywhere("abcde", "cde") // True 

And on this we finish. Now we have a partially functional regex implementation with just 106 lines. You can add some more details, but I decided not to increase the complexity without increasing the code value:

1. Character classes
2. Extract values
3. ?
4. Escape characters
5. And much more.

I hope this simple implementation will help you understand what is happening inside the regular expression engine! It is worth mentioning that the performance of the interpreter is disgusting, truly awful. Perhaps in one of the future posts I will examine the reasons for this and discuss ways to optimize ...