The sum of the sums of arithmetic progressions

We need to find out how many options exist for the location of occupied cells.
This scheme boils down to many tasks. For example, splitting a period from N + 1 calendar days into l + 1 successively smaller periods. Suppose we want to carry out an optimization calculation using the “brute force” method, calculating the objective function for each possible variation of a period in order to choose the best one. To estimate the calculation time in advance, you need to determine the number of options. This will help you decide whether to start the calculation at all. Agree - it will be useful to notify the user of your program in advance that with the parameters that he specified, the calculation will take 10,000 years.
There is a simple formula that allows for any N and l to get the number of all possible locations for occupied cells:
')
This is the formula for the sum of sums of sums ... the sum of arithmetic progressions of the form 1 + 2 + 3 + ... + n; the word “sum” in different declinations in this phrase is repeated exactly l - 1 times. In other words, this formula allows you to quickly calculate the following sums:
An ordinary desktop PC takes too much time to calculate these sums "head-on" (especially with the use of long arithmetic - and one cannot do without it).
When I first began to solve this problem (and did not yet know this formula), I scored the phrase “the sum of sums of arithmetic progressions” in a search engine and found nothing. That is how I called my article - in the hope that the next searcher for this formula will be able to quickly find it here.
I have no links to an authoritative source regarding this formula. I derived it analytically and checked it numerically, having conducted over 4000 tests. Her conclusion, if anyone is interested, is given at the end of the article.
Soon I will tell you how arithmetic progressions are related to the calculation of cell layout options, but for now I’ll give some more ready-made formulas.
We introduce an additional condition: for example, in any case, there must be at least 1 group of r adjacent unused cells. In this case, the number of options is determined as follows:
If your program carries out any calculations for each variant of the location of the cells, then the calculations for different options are probably of the same type. This means that they are easy to distribute across multiple threads. The article will explain how to organize an iteration of the options so that each thread gets an equal number of options.
1. And then the progression?
This is the easiest question. Group all the occupied cells at the left end of your row of cells - so that they follow one after the other, starting with the leftmost cell in the row:

How many options exist for the location of the rightmost of the occupied cells (we will call it the last occupied cell), provided that the remaining cells remain in place? Exactly n. Now move the PREVIOUSLY occupied cell to the right by 1 position. How many positions will be left for the last cell? n - 1. The penultimate cell can be shifted to the right n times. It means that there will be so many options for the location of the last two occupied cells: S 2 (n) = 1 + 2 + 3 + ... + n. Move the occupied cell by the third from the right to 1 position and again count the number of options for the location of the last and penultimate cells. It turns out S 2 (n - 1). The third cell can also be shifted to the right only n times, and the entire layout of the last three cells will be S 3 (n) = S 2 (1) + S 2 (2) + ... + S 2 (n).
Reasoning this way, we finally get to the number of locations for all l occupied cells:
2. Additional condition: at least 1 group of r unused adjacent cells
First consider the special cases. If n + l - 1 ≥ r (l + 1), then under no scenario do we get a variant in which there is at least 1 group of r unallocated cells. Even in the worst case - when the occupied cells in a row are evenly spaced, so that the distance between them and the edges of the row is r - 1, the number of occupied cells is simply not enough for ALL of these distances to be no more than r - 1. At least one will be at least r. Consequently:
If we fix the leftmost occupied cell in the leftmost position, the options for the location of all the other cells will be S r (l - 1) (n). If you move it 1 position to the right, the options will be S r (l - 1) (n - 1). Starting from the position r + 1, we will always have a gap of at least r length at the left end of the series, so that the remaining options can be calculated without recursion: S l (n - r). It turns out that:
Now we can proceed to the distribution of iterations by threads. To understand this, you must clearly understand how the first formula S r l (n) was derived, since This conclusion contains a specific order of iteration on the location of occupied cells.
3. How to organize iteration in several threads
The iteration order will be common to all threads. Initially, all l cells are located at the left end of the row, taking positions from 1 to l. This is the first iteration. At each iteration, the rightmost cell is shifted to the right by 1 position until it is at the end of the row, then the cell to its left position is shifted by 1 position to the right, and the outermost cell again passes all possible positions between the cell to the left and the right end of the row. When both cells are in the extreme right position, the cell to the left of them shifts 1 position to the right. And so until all the cells are at the right end of the row. During iteration, we skip the options in which there is not a single group of r adjacent unused cells.
According to this iteration order, we select the first k options and assign them to the first stream, then the next k options to the second stream, and so on. Suppose we decided to use n t flows, the number of iterations in each of which we defined as k i , i = 1, ..., n t .
The sequence number of the first iteration for each stream is called h i :
using Anylong = boost::multiprecision::cpp_int; using Opt_UVec = boost::optional<std::vector<unsigned> >; Opt_UVec arrangement(Anylong index, unsigned n, unsigned l, unsigned r = 0); The arrangement function takes the index option number and row parameters: n = N - l + 1, l and r, and returns a vector with the positions of occupied cells in the row. The position of the occupied cell is an integer from 1 to N.
The number of options grows very quickly with increasing parameters l and n, so we need a long arithmetic to represent this number. I used the class boost :: multiprecision :: cpp_int , capable of representing integers of any length.
If the index parameter exceeds the number of possible cell locations, the function returns an empty object boost :: optional . If the index parameter or the n parameter is 0, this is considered a programmer's error, and the function throws an exception.
First, translate into C ++ formulas for determining the number of options:
struct Exception { enum class Code { INVALID_INPUT = 1 } code; Exception(Code c) : code(c) {} static Exception InvalidInput() { return Exception(Code::INVALID_INPUT); } }; Anylong S(unsigned n, unsigned l) { if (!n) throw Exception::InvalidInput(); if (l == 1) return n; if (n == 1 || l == 0) return 1; Anylong res = 1; for (unsigned i = 1; i <= l; ++i) { res = res * (n + i - 1) / i; // ! } return res; } Anylong S(unsigned n, unsigned l, unsigned r) { if (!n) throw Exception::InvalidInput(); if (r == 0) return S(n, l); if (r == 1) if (n == 1) return 0; else return S(n, l); if (n + l - 1 >= r * (l + 1)) return S(n, l); if (n <= r) return 0; else if (l == 0) return 1; Anylong res = (l + 1) * S(n - r, l); for (unsigned j = 0; j <= l - 1; ++j) for (unsigned i = r; i <= n - r - 1; ++i) res -= S(i + 1, j, r) * S(n - r - i, l - j - 1); return res; } Pay attention to this line:
res = res * (n + i - 1) / i; Here the order of actions is important. The product of the factors res and (n + i - 1) is always divisible by i, and each of them separately is not. Violation of the procedure will result in distorted results.
Now there is a question and how to determine the location of the index.
Recall the order of iteration we have adopted. To move the leftmost cell 1 position to the right, you need X 1 = S r l - 1 (n) iterations. You can move it another cell to the right in X 2 = S r l - 1 (n - 1) iterations. If at some point X 1 + X 2 + ... + X i + X i + 1 turned out to be greater than index, then we have just determined the position of the first occupied cell. It must be in the i-th position. Next, we calculate how many iterations it takes to move the second cell to the right: X 1 = S r l - 2 (n - i + 1). This continues until we get to the option under the number index. If at least once i is greater than r, all subsequent calls to S r l (n) are replaced by S l (n), because we already have at least one gap of length not less than r to the left of the current cell.
It will be shorter to write code than to explain in words.
Opt_UVec arrangement(Anylong index, unsigned n, unsigned l, unsigned r = 0) { if (index == 0) throw Exception::InvalidInput(); if (index > S(n, l, r)) return {}; std::vector<unsigned> oci(l); /* occupied cells indices - ( 1 N) */ if (l == 0) return oci; if (l == 1) { assert(index <= std::numeric_limits<unsigned>::max()); oci[0] = (unsigned)index; return oci; } oci[0] = 1; unsigned N = n + l - 1; unsigned prev = 1; Anylong i = 0; auto it = oci.begin(); while (true) { auto s = S(n, --l, r); while (i + s <= index) { if ((i += s) == index) { auto it1 = --oci.end(); if (it1 == it) return oci; *it1 = N; for (it1--; it1 != it; it1--) *it1 = *(it1 + 1) - 1; return oci; } s = S(--n, l, r); assert(n); (*it)++; if (r && (*it) > prev + r - 1) r = 0; } prev = *it++; assert(it != oci.end()); *it = prev + 1; } assert(false); } 4. Derivation of formulas
Glad the lovers of school algebra with another section.
Let's start with the sum of arithmetic progressions:
Now let's return to the formula for calculating the variants with r ≠ 0:
We calculate the number of options when the gap between the last occupied cell and the right end of the row is greater than or equal to r. It is as if the last occupied cell had grown in size to r + 1, while the row sizes would have remained the same:

This number of options is S l (n - r).
Now add to it the number of options in which the gap between the last and the penultimate occupied cells is greater than or equal to r. This number of variants will again be equal to S l (n - r). But we have already counted some of these options when we calculated the previous S l (n - r). Namely, those options in which the gap between the last occupied cell and the right end of the row is greater than or equal to r. So, to the first S l (n - r) options you need to add not S l (n - r), but S l (n - r) - X, where X is the number of options in which the gap between the last and the penultimate occupied cells is greater or equal to r, as well as the gap between the last occupied cell and the right end of the row.
Exactly the same will have to be done for each j-th occupied cell - from S l (n - r) subtract X j equal to the number of options in which the gap between the j-th cell and the cell to the left of it (in the case of the leftmost cell - the interval between it and the left end of the row), as well as at least one of the intervals to the right of the j-th cell are greater than or equal to r.
In total, we have l - 1 gaps between occupied cells, plus 2 gaps between the occupied cell and the end of the row. Therefore, the term S l (n - r) appears in our formula l + 1 times. But X j is not calculated for the gap between the rightmost occupied cell and the right end of the row. Therefore, these terms will be only l.
Look at this drawing:
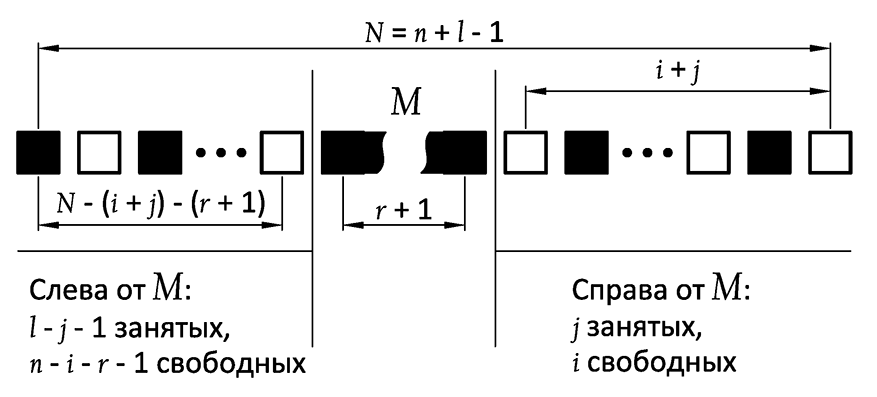
The jth cell (the one that grows to size r + 1 when iterating over j) is denoted as M. It can be in n - r possible positions, which are determined by the parameter i (i ∈ [0, n - r - 1]) . The first r positions can be disregarded, since for i <r all the intervals to the right of M will be less than r. Therefore, i ∈ [r, n - r - 1].
The number of cell locations to the right of M, in which at least 1 gap is greater than or equal to r, is equal to S r j (i + 1). The number of cell locations to the left of M is S l - j - 1 (n - i - r). The total number of variants is S r j (i + 1) ∙ S l - j - 1 (n - i - r) for all i ∈ [r, n - r - 1] and all j ∈ [0, l - 1]:
Source: https://habr.com/ru/post/348272/
All Articles