Why the logistic regression results in SAS and R do not match
Perhaps this topic will not be a discovery for experienced statisticians. However, I am sure that less experienced statistics and R-programmers will be able to discover new aspects of logistic regression, since I could find details about the reasons for the discrepancy between the results of statistical packages only in the SAS documentation.
For more than four years I have been doing biostatistics, and all this time I use the R. language in my work. RStudio makes it incredibly simple, convenient and at the same time a powerful analysis tool. However, for almost a year now I have been working in a contract research organization (CRO). Business dictates its work standards, and calculations for the vast majority of serious clinical research are performed on the SAS platform.
SAS as a language is not bad and even good at something, although it is built on the basis of a number of strange concepts from the distant 1976, the description of which could be the reason for a separate large article. The presence of these concepts in SAS today is quite understandable: leading its history from punch card work, the company now has to maintain backward compatibility with previous versions of its products, since in clinical studies the concept of reproducible research is of great importance. This makes it impossible to make radical changes to the syntax of the language, as happened between versions of Python 2.7.x and 3.x. What is really sad is the current IDE status for SAS, none of which (three in the delivery set) are even half as good as RStudio.
There is an opinion that the transition from SAS to R is much easier, but my story is the opposite. My way to learn the features of SAS is to compare the results obtained in it with R. This practice became particularly relevant after the case when, during dual programming, both SAS programmers misunderstood the manual on SAS Help and made the same error in the implementation of the method. In addition, since even the FDA uses R, it is very important that a potential validator be able to get results identical to our calculations.
')
In one study, we needed to build models based on logistic regression in order to analyze the possible relationship between a number of baseline characteristics of patients with hepatitis C and treatment success.
The task is rather trivial (but if you are not familiar with it, I suggest examples for SAS and for R with a good description of interpretation ). Questions arose when the results of the usual univariate logistic regression in several cases did not coincide between the two packages. Most often, of course, the results are the same. Sometimes it is only rounding (for example, 0.1737 and 0.1738 for p-value ). But in some cases, the difference in the values of β- coefficients and probabilities ( p-value ) is obvious.
Consider an example with the categorical predictor “Method of infection” in which the value “Blood transfusion” is chosen as the base level of the factor.
As can be seen from the example, despite the fact that the estimates of the odds ratios coincide, the values of β-coefficients in the models are different. At the same time, the values of exp (b) in SAS do not coincide with the odds ratio (OR). What is most critical for us is that the probability values ( p-value ) corresponding to the β-coefficients do not at all coincide with the results of R.
In search of the cause and the way to solve the issue, I unexpectedly discovered that the communities of users of R and SAS overlap very weakly, and in the end only the almighty Google was able to help me. Many thanks to Anne-Maria de Mars , who, with a similar comparison of the SAS results with SPSS, contacted the SAS representative and presented the solution in her blog, which allowed me to spin the chain.
The reason for the differences lies in the coding of the factor levels that are used by default statistical packets. R and SPSS use a base-level coding approach when building a model ( reference cell parameterization , you can also find reference coding or dummy coding variants) and calculate OR based on the exponentiation of β-coefficient values, while SAS uses a different approach - coding the effect ( effect parameterization or effect coding ), which uses a more complex algorithm. Detailed examples of building models for these coding schemes are presented here .
Now the OR estimates in SAS coincided completely with the exponents of the corresponding β-coefficients, and the p-value is completely identical to the results of R.
Judging by this material, SAS offers a very wide range of possible coding options for factor levels when building models. Unfortunately, I failed to find something similar in the documentation for R. I would be grateful if habrazhiteli can prompt such materials in the comments.
Introduction
For more than four years I have been doing biostatistics, and all this time I use the R. language in my work. RStudio makes it incredibly simple, convenient and at the same time a powerful analysis tool. However, for almost a year now I have been working in a contract research organization (CRO). Business dictates its work standards, and calculations for the vast majority of serious clinical research are performed on the SAS platform.
SAS as a language is not bad and even good at something, although it is built on the basis of a number of strange concepts from the distant 1976, the description of which could be the reason for a separate large article. The presence of these concepts in SAS today is quite understandable: leading its history from punch card work, the company now has to maintain backward compatibility with previous versions of its products, since in clinical studies the concept of reproducible research is of great importance. This makes it impossible to make radical changes to the syntax of the language, as happened between versions of Python 2.7.x and 3.x. What is really sad is the current IDE status for SAS, none of which (three in the delivery set) are even half as good as RStudio.
There is an opinion that the transition from SAS to R is much easier, but my story is the opposite. My way to learn the features of SAS is to compare the results obtained in it with R. This practice became particularly relevant after the case when, during dual programming, both SAS programmers misunderstood the manual on SAS Help and made the same error in the implementation of the method. In addition, since even the FDA uses R, it is very important that a potential validator be able to get results identical to our calculations.
')
Essence of the question
In one study, we needed to build models based on logistic regression in order to analyze the possible relationship between a number of baseline characteristics of patients with hepatitis C and treatment success.
The task is rather trivial (but if you are not familiar with it, I suggest examples for SAS and for R with a good description of interpretation ). Questions arose when the results of the usual univariate logistic regression in several cases did not coincide between the two packages. Most often, of course, the results are the same. Sometimes it is only rounding (for example, 0.1737 and 0.1738 for p-value ). But in some cases, the difference in the values of β- coefficients and probabilities ( p-value ) is obvious.
Consider an example with the categorical predictor “Method of infection” in which the value “Blood transfusion” is chosen as the base level of the factor.
The code and the results of R (the response is represented by the values 0 and 1):

library(haven) library(car) setwd("C:/test") adis <- read_sas("adis.sas7bdat") adis <- recode(adis, "''= NA") adis$MODEHCV = factor(adis$MODEHCV, levels = c("Blood transfusions", "Dental procedures", "Other"), ordered = FALSE) mylogit <- glm(SVR12FL ~ MODEHCV, data = adis, family = binomial(link = 'logit')) 
SAS code and results (response represented by N and Y values):
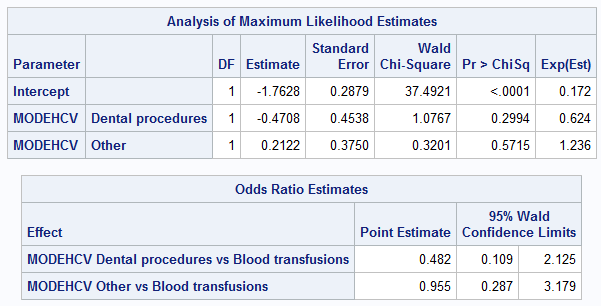
%let dir=C:\test; LIBNAME source "&dir\DataIN" access=readonly; DATA adis; set source.adis; RUN; PROC LOGISTIC data = adis; class MODEHCV (reference = 'Blood transfusions'); model SVR12FL (event = 'Y') = MODEHCV / expb; RUN; 
As can be seen from the example, despite the fact that the estimates of the odds ratios coincide, the values of β-coefficients in the models are different. At the same time, the values of exp (b) in SAS do not coincide with the odds ratio (OR). What is most critical for us is that the probability values ( p-value ) corresponding to the β-coefficients do not at all coincide with the results of R.
Decision
In search of the cause and the way to solve the issue, I unexpectedly discovered that the communities of users of R and SAS overlap very weakly, and in the end only the almighty Google was able to help me. Many thanks to Anne-Maria de Mars , who, with a similar comparison of the SAS results with SPSS, contacted the SAS representative and presented the solution in her blog, which allowed me to spin the chain.
The reason for the differences lies in the coding of the factor levels that are used by default statistical packets. R and SPSS use a base-level coding approach when building a model ( reference cell parameterization , you can also find reference coding or dummy coding variants) and calculate OR based on the exponentiation of β-coefficient values, while SAS uses a different approach - coding the effect ( effect parameterization or effect coding ), which uses a more complex algorithm. Detailed examples of building models for these coding schemes are presented here .
Change the default scheme in SAS to reference parameterization
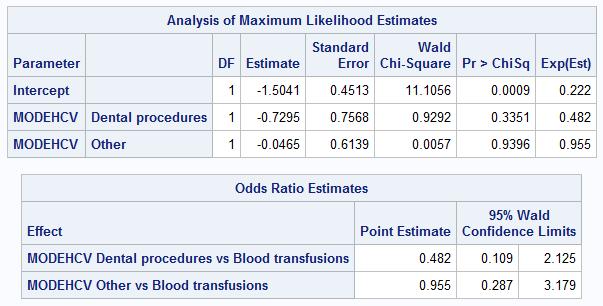
PROC LOGISTIC data = adis; class MODEHCV (reference = 'Blood transfusions') / param = ref; model SVR12FL (event = 'Y') = MODEHCV / expb; RUN; 
Now the OR estimates in SAS coincided completely with the exponents of the corresponding β-coefficients, and the p-value is completely identical to the results of R.
PS
Judging by this material, SAS offers a very wide range of possible coding options for factor levels when building models. Unfortunately, I failed to find something similar in the documentation for R. I would be grateful if habrazhiteli can prompt such materials in the comments.
Source: https://habr.com/ru/post/348244/
All Articles