Nonrandom chance, or Attack on PRNG in .NET

Random numbers should not be generated with a method chosen at random.
- Donald Knuth

Delving into the source code of one service in search of vulnerabilities, I came across the generation of a one-time code for SMS authentication. The code request handler looked like this:

class AuthenticateByPhoneHandler { /* ... */ static string GenerateCode() => rnd.Next(100000, 1000000).ToString(); readonly static Random rnd = new Random(); }

The problem is visible to the naked eye: to generate a 6-digit code, the class Random is used - a simple non-cryptographic pseudo-random number generator (PRNG). We will deal with them closely: let's learn how to predict the sequence of random numbers and estimate the possible scenario of an attack on the service.

Thread safety

By the way, note that in the above code snippet, access to a static instance of the Random class from several threads is not synchronized. This can lead to an unpleasant incident, which can often be found in questions and answers to StackOverflow:

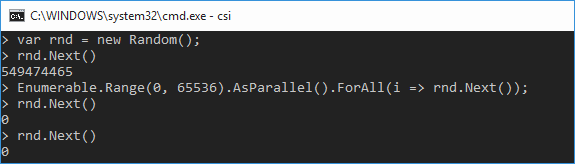
That is, the first attack scenario is simple - we send to the server a lot of parallel requests for sending SMS, as a result, an instance of the class Random is in a very poor condition.

However, this attack is too rough. In addition, to violate the performance of the service in the plans were not included. Therefore, we turn to the prediction of codes sent in SMS.

Goodbye Random.cs

The documentation says that the Random class implements the algorithm for generating random numbers using the subtraction method proposed by Donald Knuth in the second volume of “The Art of Programming”, a variation of the Fibonacci retarded generator .

It's funny that the algorithm is implemented with a typo . The generator is initialized with values that differ from those described by the Whip, therefore the properties and period of the generated numbers may be worse than expected. Microsoft decided not to fix the implementation so as not to break backward compatibility. Instead, the documentation appeared clause about the "modified" version of the algorithm.

This is the method for generating the next pseudo-random number.

 private int InternalSample() { int locINext = inext; int locINextp = inextp; if(++locINext >= 56) locINext = 1; if(++locINextp >= 56) locINextp = 1; var retVal = SeedArray[locINext] - SeedArray[locINextp]; if(retVal == int.MaxValue) retVal--; if(retVal < 0) retVal += int.MaxValue; SeedArray[locINext] = retVal; inext = locINext; inextp = locINextp; return retVal; } private int inext = 0; private int inextp = 21; private readonly int[] SeedArray = new int[56];

The generator has an internal SeedArray state of 56 SeedArray (the zero element is not used, so there are actually 55 of them). A new pseudo-random number is obtained by subtracting two numbers located in the internal state with inext and inextp . The same number replaces the element of the internal state with the inext index.

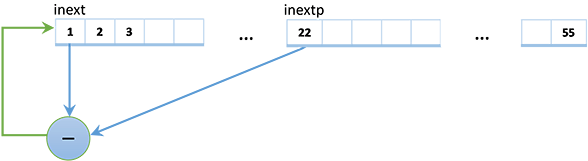
This means that in order to predict the next pseudo-random number, one does not need to know the theory of additive random generators, but rather just to know the current internal state of the generator. And this can be done on the basis of its output values.

Predict the future

As a predictor, we will use an instance of the same class Random, in which we will replace the internal state of SeedArray through reflection. To fill the internal state, we need a function inverse to converting an arbitrary Int32 number from the internal state to the range [min;max) :

 public static int GetInternalStateValue(int minValue, int maxValue, int value) { var range = maxValue - minValue; //    range > int.MaxValue return (int) ((double) (value - minValue) / range * int.MaxValue); }

In this method, operations with real numbers are used, so we only get an approximate value of the internal state. Let's write a test to find out how big the error is on our range [100000; 1000000) [100000; 1000000) :

 var rnd = new Random(31337); var seedArray = new[] {0}.Concat( //   SeedArray   Enumerable.Range(0, 55) .Select(i => rnd.Next(Min, Max)) .Select(val => GetInternalStateValue(Min, Max, val))) .ToArray(); var predictor = new Random(); typeof(Random) .GetField("SeedArray", BindingFlags.Instance | BindingFlags.NonPublic) .SetValue(predictor, seedArray); //   for(int i = 0; i < 10; i++) Console.WriteLine($"{rnd.Next(Min, Max)} vs {predictor.Next(Min, Max)}");

We get:

 103753 vs 103754 // (+1) 617169 vs 617169 523211 vs 523211 382862 vs 382862 516139 vs 516140 // (+1) 555187 vs 555187 384855 vs 384856 // (+1) 543554 vs 543553 // (-1) 327867 vs 327867 745153 vs 745153

Voila! Now you can, knowing the sequence of 55 numbers, almost accurately predict the following pseudo-random numbers from the desired range.

After the prediction (55 - 21 = 34) of numbers, the error increases, and it is better to reinitialize the predictor.

Attack scenario

For the implementation of the attack must take into account another nuance. The vulnerable service had several replicas, requests for which were randomly balanced. One could also check the randomness of balancing, but this was not required - the server’s response contained an HTTP header with the name of the service replica.

In addition, the service had a limit - no more than 3 SMS per number. However, it is easy to get around through any free service for receiving SMS, which provides a pool of phone numbers.

Now the entire mosaic assembly. The attack scenario will be as follows:

We choose the time when the service request flow is minimal to avoid pseudo-random numbers being generated by other users.
Using the phone numbers from the pool, we get N × 55 SMS with access codes, where N is the number of service replicas.
Using the GetInternalStateValue method to GetInternalStateValue convert numbers from a range, we fill the internal states of N instances of the random number generator.
We send SMS to the phone number of interest, predict the sent code, enter the service under someone else’s account.
If the code does not fit (we assume that due to an error when working with real numbers), try (+1) and (-1).
We take the next phone of interest ...

Conclusion

Predicting the future for a Random instance is a simple matter.

Prediction of the past is also not a problem. To do this, just in the same way, initialize the internal state of the generator, and then “reverse” the InternalSample method and wind back 55 already known values.

When using Random, you need to remember to synchronize access or use ThreadStatic instances. When creating multiple instances, you need to take care of the seed, so as not to get a lot of equally initialized objects.

In security-critical places, you need to use a cryptographically stable and thread-safe RNGCryptoServiceProvider and not disclose unnecessary information about the environment.