Cubic cards

Until now, we have had to use only two-dimensional textures, however, OpenGL supports many more texture types. And in this lesson we will look at the type of texture map, in fact, a combination of several separate textures - this is a cubemap .

A cubic map, in fact, is one texture object containing 6 separate two-dimensional textures, each of which corresponds to the side of a textured cube. Why can such a cube come in handy? Why stitch six separate textures into one map instead of using separate texture objects? The bottom line is that samples from a cubic map can be made using the direction vector.


Imagine a single cube (a cube with sides of 1x1x1 units) from the center of which the direction vector comes out. A texture sample from a cubic map with the orange direction vector inside would look like this:

The length of the direction vector is not important. OpenGL is enough to know the direction to conduct the correct final sample from the texture.

If we imagine the shape of the cube on which the cubic map is stretched, then it turns out that the direction vector indicating the sample area looks similar to the interpolated coordinates of the cube vertices. With this in mind, we can make samples from the map using the data of the coordinates of the cube, it is only necessary that the cube itself remains symmetrically located relative to the origin. In this case, the texture coordinates of the cube vertices can be taken equal to the position vectors of the cube vertices. As a result, the texture coordinates correctly refer to the textures of individual faces of the cube.

Create a cubic map

A cubic map, like any other texture object, is created according to the already familiar rules: we create the texture object directly and link it to a suitable texture target ( texture target ) before performing any operations on the texture. In our case, the anchor point is GL_TEXTURE_CUBE_MAP :

unsigned int textureID; glGenTextures(1, &textureID); glBindTexture(GL_TEXTURE_CUBE_MAP, textureID); 

Since the cubic card is a combination of six separate texture images, we will have to make six calls to glTexImage2D with a set of parameters similar to those used in previous lessons. This time, however, in each call, the value of the texture target parameter will take one of the special values ​​associated with each face of the cube map. In fact, we are reporting OpenGL for which of the faces we are creating a texture image. And so six times: one glTexImage2D on each side.

Since there are only six faces, OpenGL has six special texture targets, specifically responsible for creating textures for all faces of a cube map:


Often, the enumeration elements (enum) of OpenGL have numeric values ​​that vary linearly. In the case of the listed elements, this is also true. This will allow us to easily initialize textures for all faces using a simple loop that starts with a texture target of GL_TEXTURE_CUBE_MAP_POSITIVE_X and with each pass simply increases the value of the target by 1:

 int width, height, nrChannels; unsigned char *data; for(GLuint i = 0; i < textures_faces.size(); i++) { data = stbi_load(textures_faces[i].c_str(), &width, &height, &nrChannels, 0); glTexImage2D( GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data ); } 

Here we use a vector called textured_faces , which contains the paths to all the texture files needed to define a cubic map in the order corresponding to the order of identifiers of faces from the table. This will create textures for each of the faces of the currently linked cube map.

A cubic map texture object has all the same properties as any texture, so it doesn’t hurt to set up texture filtering and repeating modes:

 glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE); 

Do not be surprised at the unfamiliar GL_TEXTURE_WRAP_R parameter - it just adjusts the repetition mode on the third texture coordinate (a-z coordinate for positions). We use the GL_CLAMP_TO_EDGE repetition mode , because texture coordinates that are exactly between two edges can lead to the lack of a correct sample (due to some hardware limitations). This selected repetition mode allows you to return a value from the texture boundary, even in cases of samples between the edges of the map.

Before rendering objects using a cubic map, we must specify the used texture unit and bind the cubic map. Everything is exactly the same as in the cases with 2D textures.

In the fragment shader code, you will have to change the sampler type to samplerCube , since in the texture function we will pass a three-dimensional vector of texture coordinates instead of a two-dimensional one. An example of a shader code using a cubic map below:

 in vec3 textureDir; //  ,      uniform samplerCube cubemap; //     void main() { FragColor = texture(cubemap, textureDir); } 

Well, all this is entertaining, but for now it seems useless. Do not rush to conclusions, some wonderful effects are very easy to implement using cubic cards. One of them is the creation of a skybox.

Skybox

A skybox is a huge cube that encloses the entire current scene, which is textured by six images of the surrounding scene environment and creates for the player the illusion that the scene in which he is located is much more than it actually is. Usually skyboxes in games are realized using images of mountains, a cloudy or night sky - all this, I think, is familiar to you. For example, a skybox with a night sky texture from the third part of TES:


I think you have already guessed that the cubic cards simply ask themselves to be used here: we have a cube with six edges and the need to correctly texture it in accordance with the edge. In the previous screenshot, only a few images of the night sky gave the player the effect of being in a huge universe, although in reality he is a prisoner of a tiny cube.

There are enough resources in the network where you can find texture sets prepared for skyboxes. For example, here and here they are enough for many experiments. Often, the skybox textures laid out on the network follow the following presentation:


If you fold the image along the boundaries (bending the edges “behind the screen”), then a completely ottuksturirovanny cube will be released, inside which a feeling of large space is created. Some resources follow this texture layout, so you will need to cut six textures for individual faces. But, in most cases, they are laid out with a set of six separate images.

Here in good resolution you can download the texture for the skybox, which we will use in the lesson.

Skybox download

Since a skybox is represented as a cubic map, the loading process is not much different from what was already mentioned in the lesson. The following function is used for loading. It accepts a vector with six paths to texture files:

 unsigned int loadCubemap(vector<std::string> faces) { unsigned int textureID; glGenTextures(1, &textureID); glBindTexture(GL_TEXTURE_CUBE_MAP, textureID); int width, height, nrChannels; for (unsigned int i = 0; i < faces.size(); i++) { unsigned char *data = stbi_load(faces[i].c_str(), &width, &height, &nrChannels, 0); if (data) { glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data ); stbi_image_free(data); } else { std::cout << "Cubemap texture failed to load at path: " << faces[i] << std::endl; stbi_image_free(data); } } glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE); glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE); return textureID; } 

The function code should not be a surprise. This is all the same code for working with a cubic card that was shown in the previous section, but put together in one function.

 vector<std::string> faces; { "right.jpg", "left.jpg", "top.jpg", "bottom.jpg", "front.jpg", "back.jpg" }; unsigned int cubemapTexture = loadCubemap(faces); 

Before calling the function itself, it is necessary to fill in the vector with the paths to the texture files, and in the order corresponding to the order of descriptions of the elements of the OpenGL enumeration describing the order of the faces of the cube map.

Skybox display

Since we cannot do without a cube object, we will need new VAO, VBO and an array of vertices, which can be downloaded here .

Samples from the cube map used to cover a three-dimensional cube can be made using the coordinates on the cube itself. When a cube is symmetric about the origin, then each of the coordinates of its vertices also specifies the direction vector from the origin. And this direction vector is used to select from the texture at the point corresponding to the top of the cube. As a result, we don’t even have to pass texture coordinates to the shader!
For the render you will need a new set of shaders, quite simple. The vertex shader is trivial, only one vertex attribute is used, without texture coordinates:

 #version 330 core layout (location = 0) in vec3 aPos; out vec3 TexCoords; uniform mat4 projection; uniform mat4 view; void main() { TexCoords = aPos; gl_Position = projection * view * vec4(aPos, 1.0); } 

The interesting point here is that we reassign the input coordinates of the cube to a variable containing the texture coordinates for the fragment shader. The fragment shader uses them for sampling with the samplerCube :

 #version 330 core out vec4 FragColor; in vec3 TexCoords; uniform samplerCube skybox; void main() { FragColor = texture(skybox, TexCoords); } 

And this shader is pretty simple. We take the transmitted coordinates of the vertices of the cube as texture coordinates and make a selection from the cube map.

The render also does not contain anything tricky: we bind the cubic map as the current texture and the skybox sampler immediately receives the necessary data. We will produce the skybox output first of all the objects in the scene, and also disable the depth test. This ensures that the skybox will always be on the background of other objects.

 glDepthMask(GL_FALSE); skyboxShader.use(); // ...      glBindVertexArray(skyboxVAO); glBindTexture(GL_TEXTURE_CUBE_MAP, cubemapTexture); glDrawArrays(GL_TRIANGLES, 0, 36); glDepthMask(GL_TRUE); // ...    

If you try to start the program right now, you will encounter the following problem. In theory, we would like the skybox object to remain positioned symmetrically relative to the player’s position, no matter how far he moves - only there you can create the illusion that the environment depicted on the skybox is really huge. But the view matrix that we use applies a complete set of transformations: rotation, scaling, and movement. So if a player moves, the skybox also moves! In order for the player’s actions not to affect the skybox, we would have to remove the movement information from the view matrix.

Perhaps you will recall the introductory lesson on lighting and the fact that we were able to get rid of information about the movement in 4x4 matrices by simply extracting the 3x3 submatrix. You can repeat this trick by simply casting the dimensionality of the species matrix first to 3x3, then back to 4x4:

 glm::mat4 view = glm::mat4(glm::mat3(camera.GetViewMatrix())); 

The data on the offset will be removed, but the data of the other transformations will remain, which will allow the player to look normally around.

As a result, we get a picture that conveys the feeling of large space due to the skybox. Having flown near the container you will feel this sense of scale, which rather adds realism to the whole scene:


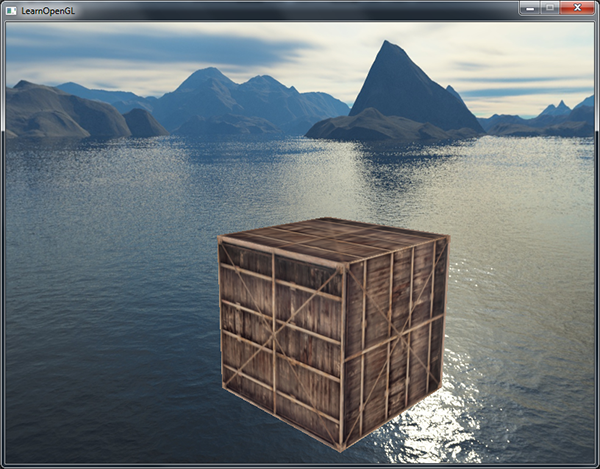
Try different texture selections and appreciate the effect they have on the sensations from the scene.

Skybox render optimization

As noted, the skybox is rendered in front of all the other objects in the scene. Works with a bang, but not too economically on resources. Judge for yourself: when outputting in advance, we will have to execute a fragmentary shader for all pixels of the screen, although in the final scene only some of them will remain visible, and most could be discarded using an early depth test, saving us valuable resources.

So, for efficiency reasons, the skybox should be displayed last. In this case, the depth buffer will be filled with the depth values ​​of all the objects in the scene, and the skybox will only be displayed where the early depth test was successful, saving us the challenges of the fragment shader. But there is a catch: most likely nothing will get into the frame at all, since the skybox is just a 1x1x1 cube and it will fail most of the depth tests. It is also impossible to disable the depth test before rendering, because the skybox will simply be displayed over the stage. You need to force the depth buffer to believe that the depth of the entire skybox is 1, so that the depth test fails if there is another object in front of the skybox.

In the lesson on coordinate systems, we mentioned that the perspective division is made after the execution of the vertex shader and produces the division of the xyz components of the vector gl_Positions by the value of the component w . Also, from the depth test, we know that the component z obtained after dividing is equal to the depth of the given vertex. Using this information, we can set the z component of the vector gl_Positions to be the component w , which, after perspective division, will give us a depth value everywhere equal to 1:

 void main() { TexCoords = aPos; vec4 pos = projection * view * vec4(aPos, 1.0); gl_Position = pos.xyww; } 

As a result, in the normalized coordinates of the device, the vertex will always have a component z = 1, which is the maximum value in the depth buffer. And the skybox will be displayed only in areas of the screen where there are no other objects (only here the depth test will be passed, because at other points the skybox overlaps something).

However, we need to change the type of the depth function to GL_LEQUAL instead of the standard GL_LESS . The cleaned depth buffer is filled with the default value of 1, as a result, it is necessary to ensure that the skybox passes the test for depth values ​​not strictly smaller than those stored in the buffer, but less or equal.

The code using this optimization can be found here .

Environment mapping

So, a cubic map contains information about the surroundings of the scene, projected into one texture object. Such an object can be useful not only for the manufacture of skyboxes. Using a cubic map with a surrounding texture, you can simulate the reflective or refractive properties of objects. Such techniques that use cubic maps are called environment mapping techniques and the most widely known of them: imitation of reflection and refraction.

Reflection

Reflection is the property of an object to display the surrounding space, i.e. Depending on the angle of observation, the object acquires colors that are more or less identical to those of the environment. The mirror is a perfect example: it reflects the environment depending on the direction of the observer’s gaze.

The basics of physics of reflections are not too complicated. The following image shows how to find the reflection vector and use it to sample from a cubic map:


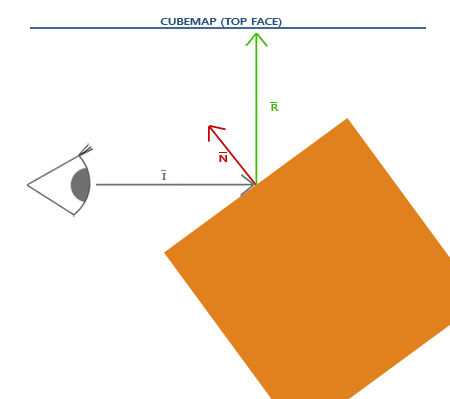
Reflection vector $$$\ color {green} {\ bar {R}}$is based on the direction of sight $$$\ color {gray} {\ bar {I}}$relative to the normal vector $$$\ color {red} {\ bar {N}}$. Direct calculation can be carried out using the built-in GLSL reflect () function. The resulting vector $$$\ color {green} {\ bar {R}}$then it can be used as a direction vector for sampling a reflected color value from a cube map. As a result, the object will look as if it reflects the skybox surrounding it.

Since the skybox in our scene has already been prepared, the creation of reflections is not very difficult. Slightly modify the fragment shader used by the container to give it reflective properties:

 #version 330 core out vec4 FragColor; in vec3 Normal; in vec3 Position; uniform vec3 cameraPos; uniform samplerCube skybox; void main() { vec3 I = normalize(Position - cameraPos); vec3 R = reflect(I, normalize(Normal)); FragColor = vec4(texture(skybox, R).rgb, 1.0); } 

First, we calculate the direction vector of the camera (glance) I and use it to calculate the reflection vector R , which is used for sampling from the cube map. We again use the interpolated Normal and Position values, so we have to clarify the vertex shader as well:

 #version 330 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 aNormal; out vec3 Normal; out vec3 Position; uniform mat4 model; uniform mat4 view; uniform mat4 projection; void main() { Normal = mat3(transpose(inverse(model))) * aNormal; Position = vec3(model * vec4(aPos, 1.0)); gl_Position = projection * view * model * vec4(aPos, 1.0); } 

Since normals are used again, their transformation requires the return of the use of the matrix of normals. Position vector contains world coordinates of a vertex. It will be used in the fragment shader to calculate the gaz direction vector.

Due to the presence of the normals, you will have to update the vertex data array used as well as update the code associated with the configuration of the vertex attribute pointers. Also, do not forget to set the cameraPos uniform for each iteration of the render.

Before the withdrawal of the container, you should bind the object of the cubic map:

 glBindVertexArray(cubeVAO); glBindTexture(GL_TEXTURE_CUBE_MAP, skyboxTexture); glDrawArrays(GL_TRIANGLES, 0, 36); 

As a result of the program, we get a cube, leading as a perfect mirror, reflecting the whole environment.


The source code is here .

When a similar special effect is assigned to an entire object, it looks like it is made of highly reflective material like polished steel or chrome. If you load a nanosuit model from a lesson on model loading , then the whole suit will look all-metal:


It looks awesome, but in reality it is rarely what object is completely mirrored. But you can put in the use of a reflection map that will add a bit more detail to the models. Like diffuse and specular maps, this type of map is a regular texture, the selection of which determines the degree of specular reflection for the fragment. With their help, you can specify areas of the model that have a mirror image and its intensity. In the exercises for this lesson, you will be offered the task of adding a reflection map to the model loader developed earlier.

Refraction

Another form of displaying the environment is refraction, which is somewhat similar to reflection. Refraction is a change in the direction of movement of a beam of light caused by its transition through the interface between two media. It is refraction that gives the effect of changing the direction of light in liquid media, which is easily noticeable if you submerge half of the hand.

Refraction is described by Snell's law , in combination with a cubic map that looks like the following:


Again, we have a vector of observation $$$\ color {gray} {\ bar {I}}$normal vector $$$\ color {red} {\ bar {N}}$and the final refraction vector $$$\ color {green} {\ bar {R}}$. As can be seen, the direction of the gaze vector is distorted due to refraction. And it is the modified vector $$$\ color {green} {\ bar {R}}$will be used to sample from the cube map.

The refraction vector is easy to calculate using another GLSL built-in function - refract () , which takes the normal vector, the gaze direction vector and the ratio of the refractive indices of the adjacent materials.

The refractive index determines the degree of deviation of the direction of the beam of light that follows through the material. Each substance has its own coefficient, here are a few examples:


The data from the table are used to calculate the relationship between the refractive indices of the materials through which the light passes. In our case, the beam passes from the air into the glass (we will agree that our container is glass), so the ratio is 1 / 1.52 = 0.658.

The cubic map is already attached to us, the vertex data, including the normals, are loaded, and the camera position is transferred to the corresponding uniforms. It only remains to change the fragment shader:

 void main() { float ratio = 1.00 / 1.52; vec3 I = normalize(Position - cameraPos); vec3 R = refract(I, normalize(Normal), ratio); FragColor = vec4(texture(skybox, R).rgb, 1.0); } 

By changing the values ​​of the refractive indices, you can create completely different visual effects.When launching the application, unfortunately, we are not waiting for a particularly impressive picture, since the glass cube does not emphasize the refractive effect too much and just looks like a cubic magnifying glass. Another thing, if you use the nanosuit model - it becomes immediately clear that the object is made of a substance like glass:


It can be imagined that with the help of masterly application of lighting, reflection, refraction and transformation of the peaks, a very impressive simulation of the water surface can be achieved.

However, it is worth noting that for physically reliable results we will need to simulate the second refraction as the beam exits from the back side of the object. But for simple scenes, even a simplified refraction, taking into account only one side of the object, is quite enough.

Changing Environment Maps

In this lesson, we learned to use a combination of several images to create a skybox, which, although it looks great, does not take into account the possible presence of moving objects in the scene. Now it is imperceptible, since there is a single object in the scene. But if there is a reflecting object in the scene, surrounded by other objects, we would see only a reflection of the skybox, as if there were no other objects.

Using off-screen frame buffers, it is possible to create a new cubic scene map from the point of standing of the reflecting object by rendering the scene in six directions. Such a dynamically created cubic map could be used to create realistic reflective or refracting surfaces in which other objects are visible. This technique is called the dynamic display of the environment, since we are preparing new cube maps, including the whole environment, right on the fly, in the rendering process.

The approach is wonderful, but with a significant drawback - the need for a sixfold rendering of the entire scene for each object using a cubic environment map. This is a very significant blow to the performance of any application. Modern applications are trying to make the most of static skyboxes and pre-calculated cubic maps, where possible, for an approximate implementation of the dynamic display of the environment.

Despite the fact that dynamic mapping is a great technique, you have to use a lot of tweaks and resourceful hacks to apply it in an application without significant performance drawdown.

Exercises

Try adding a reflection map to the model uploader created in the appropriate tutorial . These models of nanosuit, including the very texture of the reflection map, can be downloaded here . I will note a few points:

• Assimp obviously doesn’t like reflection maps in most of the model formats, so we’ll cheat a bit - we’ll store the reflection map as a background light map. Loading the map, respectively, will have to be performed with the transfer of the aiTextureType_AMBIENT texture type in the material loading procedure.
• A reflection map hastily created from a specular gloss map. Therefore, in some places it is not well superimposed on the model.
• Since the model loader already uses three texture units in the shader, you will have to use the fourth unit to bind the cube map, since the sample is taken from the same shader.

If everything is done correctly, the result will be as follows:


From the translator :

It is worth noting that when working with scans for skyboxes, you can run into significant orientation confusion, especially when naming textures by face names (“left”, “right”, ...), and not along axes directions (+ X - positiveX, posX; -X - negativeX, negX, ...).
This is a consequence of the fact that the specification of the expansion of cubic maps is rather ancient and goes to the specification of Pixar's RenderMan, where the cubic map uses a left-handed coordinate system and the cube itself collapses as if the observer were in the center. The very same OpenGL, as we remember, uses the right-handed coordinate system.

We will have to recollect this either if the scan of the texture of interest does not match the one described here, or if there is a need to align the “sides” of the cubic map relative to the world coordinates, as if it was collapsed with the observer inside.

On the “cross” of the “cross” in the “Skybox” section, the front edge is considered as such from the point of view of the observer who is outside the cube, looking directly at him. In the code, it is loaded into the target corresponding to the positive semi-axis Z (in world coordinates). In the application, however, it turns out that from the inside of the cube we see an image mirrored along the X axis relative to what is depicted on the texture.

The author himself gives a link to this.the site where the scan used does not match the one shown in the lesson. To bring them into line, you have to swap the right and left panels, turn the top panel clockwise by 90 °, and the bottom panel counterclockwise.


Sweeps from this site are signed in accordance with the directions of the axes, and not the names of the faces. All that is required is to rename the files in accordance with the local table.

Understanding the essence is easier in action - in the assembled application. Sign images of cutting the skybox with the intended parties (out of curiosity, you can add texture axes) and see in the application how this will actually turn out.

PS : We have a telegram-konf to coordinate transfers. If there is a desire to fit into the cycle, then you are welcome!