What is common in the interview coder and the game "Snake"?

If you were born in the 80s or 90s, you probably heard about Snake . That is, most likely, you spent an insane amount of time on your Nokia 3310, growing a huge snake on a small small screen. What else do we remember about Nokia phones?

Their non-retractable battery, right? How did such a "primitive" phone withstand long hours of playing "Snake" without discharging the battery?

The short (and incomplete) answer: it's all about the sliding window method.
')
We would love to write an entire article about Snake , but in this post we will nevertheless consider a less spectacular, but nonetheless very important method, and answer questions like:

• Why do we and other programmers consider it a fundamental algorithm?
• Why is it used so often in technical interviews?
• How was it used in Snake and other “real” applications?
• What are the most popular interview questions you can (better) answer using the sliding window method?

If you are preparing for an interview, reading an article out of interest, or want to learn something new, then continue to read. In this case, you can safely skip the extra and move on to the most interesting sections.

NB: If you are only worried about the “Snake” (and we fully understand you), then you can go to the very end of the post.

---

Let's get started.

Despite the complexity of algorithmic programming, there is a rather short list of principles necessary for solving problems. One of these principles is the sliding window method .


Figure 1. Sliding Window

Window paradigm

The sliding window method emerged from the more general principle of framing.

Cropping is to obtain the state of the system and limit the field of view only to its part, called the “window”. This creates a separation between the framing algorithm and the algorithm applied to those elements that are visible through the window, which simplifies both algorithms.

A special case is a state consisting of a sequence of objects, for example, an array or a string. If we specify a window, we will see a subsequence. Now we can apply any processing to this limited interval, as if the sequence no longer contains any values. By limiting the interval, we make the whole task smaller . Now consider the sliding property: move the window one position to the right, and get another subsequence, to which you can also apply processing.

And here begins our adventure. If we apply the algorithm to each window separately, then we end up with a brute force tactic.

However, the beauty of the sliding window method is that it allows you to change the structure of the algorithm in such a way that it takes advantage of the window offset process itself . And the purpose of all this is to create better and faster algorithms.

We can increase the speed of execution of almost any algorithm applied to a sliding window, at least theoretically . When the window is shifted, only two elements change. The oldest is eliminated, and the newest one gets into the frame.


Figure 2. Element Shift (Red: Out, Green: Arrived)

If a rough search requires k steps to process a single window of length k , and there are n windows in a sequence, then to perform the work, the rough search algorithm requires n·k steps. But since with each step only two elements change, we can achieve a total execution time approximately proportional to 2n .

If we say that a simple passage through the sequence takes O(n) , then this means that in a general sequence no algorithm can be faster than O(n) . This analysis has shown us that the correct application of the sliding window method can lead to the invention of complete sequence processing algorithms that can be performed in O(n) .

In other words, he promises us that we can invent perfect algorithms for solving the problem, which can not be faster!

Having finished with the necessary introduction, we consider three programming problems that can be solved using this general concept of algorithms, and show specific examples of how they were used in real cases.

Programming Task 1: Moving Average

The task that needs to be solved is to create an algorithm that calculates the moving average of a number series.

For a given row a0, a1, … an-1 and the parameter k, 0 < k <= n we must generate a new sequence, such that each element is the average value of k consecutive elements of the original sequence:


Figure 3. Eq Average

Context: moving average is useful for smoothing the flow of input data. If the numbers are affected by noise, then the raw data will be difficult to display. As can be seen from the two illustrations below, smoothing provides a more informative scheme.


Figure 4. Moving average smooths input data

This problem can be effectively solved using the sliding window method. He immediately reveals a common feature of most of these algorithms: the first k-1 elements do not create output data. Only when filling the entire window, we can get the first portion of the results. All subsequent windows create one result each. Therefore, a sequence of n elements using a sliding window algorithm creates a sequence of n-k+1 results.

Now for the implementation. The average value of a window is the sum of all elements divided by the length of the window.


Figure 5. Eq Sum

With this formulation, we can immediately see the advantage of using the sliding window method. The sum of the window values ​​can be calculated from the sum of the values ​​of the window preceding it:


Figure 6. Eq Optimization

The calculation of the sum of the first window takes k steps, and for each of the next window only two additional operations are required.

The following shows the implementation of this response in C ++, passing the first k elements to create the first output. All other output numbers are calculated using the optimized summation formula.

 double* moving_average(double* data, int n, int k) { assert(data != NULL); assert(n > 0); assert(0 < k && k <= n); double* result = new double[n — k + 1]; double sum = 0; for (int i = 0; i < k; i++) { sum += data[i]; } result[0] = sum / k; for (int i = k; i < n; i++) { sum = sum — data[i — k] + data[i]; result[i — k + 1] = sum / k; } return result; } 

The main point of this algorithm is that each element in the original sequence is processed a maximum of twice, which creates a total time complexity O(n) .

Programming Task 2: Maximum Sum Subsequence

The task that needs to be solved is to create an algorithm for finding a subsequence with the largest sum of all possible subsequences.

This can be a real problem if the input data contains negative values.

And here again you can use the sliding window method to create a solution with the execution time O(n) . Only this time the window length will not be constant. In fact, since the task itself is to find the most suitable window, the window length can change in the process.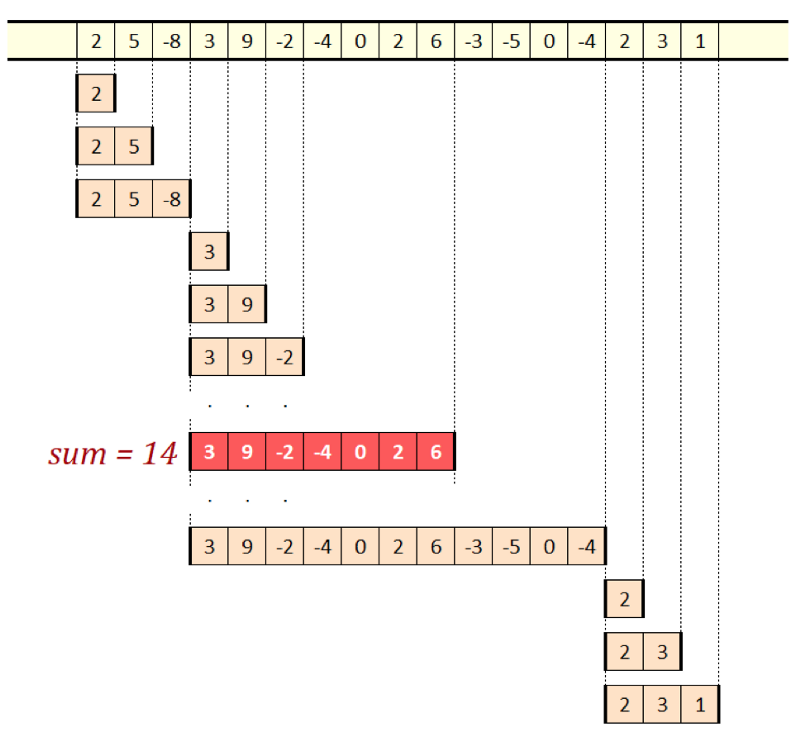


Figure 7. Maximum amount, solution with sliding windows

The idea is to watch what happens when we already have a window with a certain amount. Then we want to add the following value. This value can be added to the amount of the window. But it can also be taken as a completely new window of unit length. Ask a question: which of them will have a greater amount? Whatever it is, we will save it as a new window and move to the next input value, repeating the same procedure. Look at the picture above, which shows how the windows gradually slide along the sequence.

The winning option will always be a subsequence with a maximum amount ending on the current input element. Each window is discarded immediately when its sum becomes negative: this is a situation in which the number alone is better than in combination with the maximum preceding window.

We are left with the only last step - the determination of a common maximum. Candidates are all windows because they slide towards the end of the sequence. After the completion of the sequence, the window with the highest amount will be the subsequence with the maximum amount.

Below is a straightforward implementation of the algorithm in C ++. And again, each element of the sequence is considered no more than two times, which is the total time complexity of the function O(n) .

 std::tuple<int, int, int> max_sum_subsequence(int* data, int n) { assert(data != NULL); assert(n > 0); int bestStart = 0; int bestLength = 1; int maxSum = data[0]; int curStart = bestStart; int curLength = bestLength; int curSum = maxSum; for (int i = 1; i < n; i++) { if (curSum < 0) { curStart = i; curLength = 1; curSum = data[i]; } else { curLength += 1; curSum += data[i]; } if (curSum > maxSum) { bestStart = curStart; bestLength = curLength; maxSum = curSum; } } return std::tuple<int, int, int>(bestStart, bestLength, maxSum); } 

Programming objective 3: maxima of all k-subsequences

The task that needs to be solved is to create an algorithm that calculates the maxima of all subsequences of length k in a numerical sequence of length n . Note: this is a difficult task.

This algorithm is used in image processing, where, as you can guess, algorithms with the execution time O(n) are valued most of all others.


Figure 8. Maximums

When the window slides, it creates the maximum value contained in the output. The difficult part of the solution is that there is no formula giving the maximum of a given window. We can take as result one of the elements.

But it cannot be said that we cannot benefit from the use of the sliding window method. This is the idea: suppose we have a window with four values, as shown in the figure above.

When an additional value enters the frame, we need to understand how it relates to the existing values. To begin with, if you continue sliding the window, all previous values ​​fall out of it before this new value falls out. This is an important conclusion. If the previous value is less than the new, then it will never be the maximum, simply because the new, larger value will always overshadow it.


Figure 9. Maximum slip

This leads us to the idea of ​​not recognizing each new value and removing all the smaller values ​​that it finds in the window when the window slides, as shown in the figure below. This operation has another consequence.

If each value added to the right removes all smaller values, then the window will contain only a non-increasing, discontinuous subsequence of the original window. Another consequence is that it is now becoming obvious - the leftmost element of the window is the maximum value that we need to calculate.


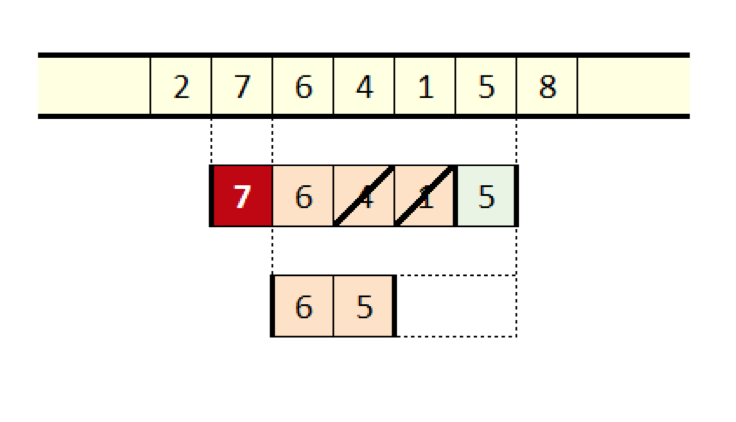
Figure 10. Maximum screening.

It is necessary to clarify one more detail. When the window slides, the leftmost value of the sequence drops out. This value could already have been removed by a larger value. Or it could survive all the values ​​following it on the right. In the latter case, the value from the input data will be the leftmost value in the frame, and now it is time to delete it.

The figure below shows the entire process applied to a sequence of seven elements with a window length of four.


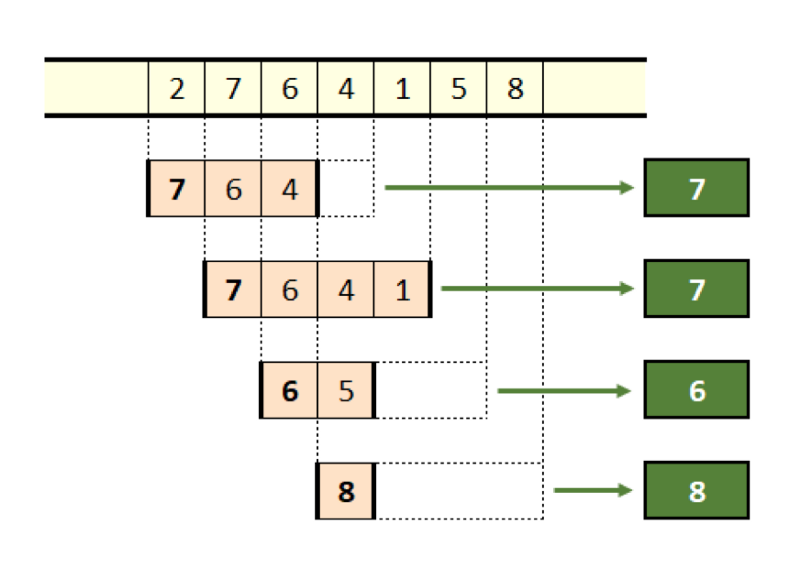
Figure 11. Maximums total

At this point, we complete the description of the algorithm and begin its implementation. The normal implementation is based on a dequeue. Dequeue supports adding to and removing from both sides of the queue, and we use these operations to implement the algorithm.

 void insert_maximum_candidate(int value, bounded_deque<int> &maximums) { while (!maximums.empty() && maximums.back() < value) maximums.pop_back(); maximums.push_back(value); } void remove_maximum_candidate(int value, bounded_deque<int> &maximums) { if (!maximums.empty() && maximums.front() == value) maximums.pop_front(); } int* range_maximums(int* data, int n, int k) { assert(data != NULL); assert(n > 0); assert(0 < k && k <= n); bounded_deque<int> maximums(k); for (int i = 0; i < k — 1; i++) insert_maximum_candidate(data[i], maximums); int* result = new int[n — k + 1]; for (int i = k — 1; i < n; i++) { insert_maximum_candidate(data[i], maximums); result[i — k + 1] = maximums.front(); remove_maximum_candidate(data[i — k + 1], maximums); } return result; } 

In this solution, we use our own implementation of Dequeue called fixed_deque . Unlike std::deque , this class maintains a buffer for data of a fixed length that speeds up execution by at least one order of magnitude. Inside it works as a ring buffer, which is extremely efficient. Anyway, the fixed_deque class has the same public interface as std::deque (the only difference is that its constructor expects a buffer size) and if you wish, you can replace it with std::deque . In addition to a significant reduction in the speed of execution, there will be no other consequences.

As in the previous examples, we can analyze the time complexity of this implementation. Each value from the input sequence is subjected to queuing and deletion from it no more than once. That is, a maximum of two operations are performed on one input number, and the total time complexity of the algorithm is O(n) . Also, this algorithm requires additional space O(k) , where k is the window length. (It is worth noting that previous algorithms only needed O(1) spaces.)

Think outside the box

We considered three algorithms based on the sliding window method. As we promised, each of them is executed in O(n) . I would also like to show you how the same method is applied in two completely different areas.

First, in packet routing protocols such as TCP / IP, a sliding window is used to negotiate the Internet Protocol (IP) with the Transmission Control Protocol (TCP). IP can never guarantee that packets will be received in the same order in which they were sent. At the same time, TCP just provides this guarantee. Here, a sliding window is becoming one of the most important components of the success of the TCP / IP protocol bundle.

The TCP receiver supports the expected packet window. Packets arrive at a less perfect (but more realistic) IP, and may not come in the order needed to fill the corresponding window positions. However, as soon as the leftmost packet arrives, the TCP window shifts as far as possible to the right, confirms to the sender that all adjacent packets have been received and sends them to the output. This, in turn, signals the sender about the possibility of starting the transmission of subsequent packets to the IP network.


Figure 12. TCP-IP

You have already guessed what the second (and last) example will be devoted to.

Of course, "Snake" . When this game appeared a few decades ago, most knew it on Nokia cell phones.


Figure 13. Snake

Guess? The snake itself is a sliding window! When the snake moves, it is enough for us to draw only two blocks on the screen - the tail becomes a background block, and the former background in front of the snake's head becomes a new head.


Figure 14. "Snake" = sliding window

The result of the sliding window method is that each frame of the game costs us to draw a maximum of two primitive blocks, regardless of the length of the snake. This made it possible to implement the game on a primitive "hardware" without unnecessary battery consumption.

Summarize

In this article, we analyzed a general algorithm called a sliding window. You have learned that this technique can be used to optimize data sequence processing algorithms. With a successful application, the technique provides the creation of algorithms that are executed during O(n) for a sequence of n objects, which is the most optimal design of the algorithms.

As concrete examples of solving problems, we developed three different algorithms that work with numerical sequences. All of these algorithms are used in the real world for general data processing and image processing. This explains why the sliding window method has survived to our days and remains a useful tool in creating algorithms. Therefore, you will most likely hear about him on technical interviews.