My favorite algorithm: finding the median for linear time

Finding the list median may seem like a trivial task, but performing it in linear time requires a serious approach. In this post I will talk about one of my favorite algorithms - finding the list median for deterministic linear time using the medians of the medians. Although the proof that this algorithm is performed in linear time is rather difficult, the post itself will be clear to readers with an initial level of knowledge about the analysis of algorithms.

Finding the median for O (n log n)

The most straightforward way to find the median is to sort the list and select the median by its index. The fastest sorting by comparison is performed in O(n log n) , therefore execution time ¹ , ² depends on it.

 def nlogn_median(l): l = sorted(l) if len(l) % 2 == 1: return l[len(l) / 2] else: return 0.5 * (l[len(l) / 2 - 1] + l[len(l) / 2])

This method has the easiest code, but it is definitely not the fastest.

Finding the median for the average time O (n)

Our next step is to find the median on average for linear time, if we are lucky. This algorithm, called “quickselect,” was developed by Tony Hoare, who also invented a sorting algorithm with a similar name, quicksort. This is a recursive algorithm, and it can find any element (not just the median).

Choose a list index. The method of choice is not important, in practice it is quite suitable and random. The element with this index is called the reference element (pivot) .
We divide the list into two groups:
1. Items less than or equal to pivot, lesser_els
2. Items strictly larger than pivot, great_els
We know that one of these groups contains a median. Suppose we are looking for the kth element:
- If there are k or more elements in lesser_els , recursively lesser_els list lesser_els for the k- lesser_els element.
- If lesser_els less than k elements, recursively greater_els list. Instead of searching for k, we look for k-len(lesser_els) .

Here is an example of an algorithm that runs on 11 elements:
')

    .    . l = [9,1,0,2,3,4,6,8,7,10,5] len(l) == 11,             (pivot).      3.       2.      pivot: [1,0,2], [9,3,4,6,8,7,10,5]    . 6-len(left) = 3,                  : [9,3,4,6,8,7,10,5]     ,    pivot.    2,     l[2]=6     pivot: [3,4,5,6] [9,7,10]     ,   ,                : [3,4,5,6]     ,    pivot.    1,     l[1]=4     pivot: [3,4] [5,6]     ,   ,       .        : [5,6]        ,        .    ,   5. return 5

To find the median using quickselect, we will highlight the quickselect into a separate function. Our quickselect_median function will call quickselect with the necessary indices.

 import random def quickselect_median(l, pivot_fn=random.choice): if len(l) % 2 == 1: return quickselect(l, len(l) / 2, pivot_fn) else: return 0.5 * (quickselect(l, len(l) / 2 - 1, pivot_fn) + quickselect(l, len(l) / 2, pivot_fn)) def quickselect(l, k, pivot_fn): """  k-    l (  ) :param l:    :param k:  :param pivot_fn:   pivot,     :return: k-  l """ if len(l) == 1: assert k == 0 return l[0] pivot = pivot_fn(l) lows = [el for el in l if el < pivot] highs = [el for el in l if el > pivot] pivots = [el for el in l if el == pivot] if k < len(lows): return quickselect(lows, k, pivot_fn) elif k < len(lows) + len(pivots): #       return pivots[0] else: return quickselect(highs, k - len(lows) - len(pivots), pivot_fn)

In the real world, Quickselect performs well: it consumes almost no resources and runs on average for O(n) . Let's prove it.

Proof of the mean time O (n)

On average, pivot splits the list into two approximately equal parts. Therefore, each subsequent recursion operates with ¹ ⁄ ₂ data from the previous step.

C = n + f r a c n 2 + f r a c n 4 + f r a c n 8 + . . . = 2 n = O (n)

$C = n + \ frac {n} {2} + \ frac {n} {4} + \ frac {n} {8} + ... = 2n = O (n)$

There are many ways to prove that this series converges to 2n. Instead of bringing them here, I refer to a wonderful Wikipedia article dedicated to this infinite series.

Quickselect gives us linear velocity, but only on average. What if we are not satisfied with the average, and we want guaranteed algorithm execution in linear time?

Deterministic O (n)

In the previous section, I described quickselect, an algorithm with an average speed of O(n) . “Medium” in this context means that, on average, the algorithm will be executed in O(n) . From a technical point of view, we may be very unlucky: at each step we can choose the largest element as the pivot. At each stage we will be able to get rid of one element from the list, and as a result we will get the speed O(n^2) , but not O(n) .

With this in mind, we need an algorithm for the selection of reference elements . Our goal will be to choose for linear time pivot, which in the worst case removes a sufficient number of elements to ensure the speed O(n) when used together with quickselect. This algorithm was developed in 1973 by Bloom (Blum), Floyd (Floyd), Pratt (Pratt), Rivest (Rivest) and Tarjan (Tarjan). If my explanation is not enough for you, you can study their 1973 article . Instead of describing the algorithm, I will comment on my implementation in Python in detail:

 def pick_pivot(l): """   pivot    l      O(n). """ assert len(l) > 0 #   < 5,    if len(l) < 5: #           . #            ,   #          # . return nlogn_median(l) #   l    5 . O(n) chunks = chunked(l, 5) #       ,    . O(n) full_chunks = [chunk for chunk in chunks if len(chunk) == 5] #     .     ,    #   .     n/5 ,   #  O(n) sorted_groups = [sorted(chunk) for chunk in full_chunks] #      2 medians = [chunk[2] for chunk in sorted_groups] # ,   ,    ,   #       O(n). #      n/5,     O(n) #      pick_pivot    pivot  # quickselect. O(n) median_of_medians = quickselect_median(medians, pick_pivot) return median_of_medians def chunked(l, chunk_size): """  `l`    `chunk_size`.""" return [l[i:i + chunk_size] for i in range(0, len(l), chunk_size)]

Let's prove that the median median is a good pivot. It will help us if we present the visualization of our algorithm for selecting support elements:

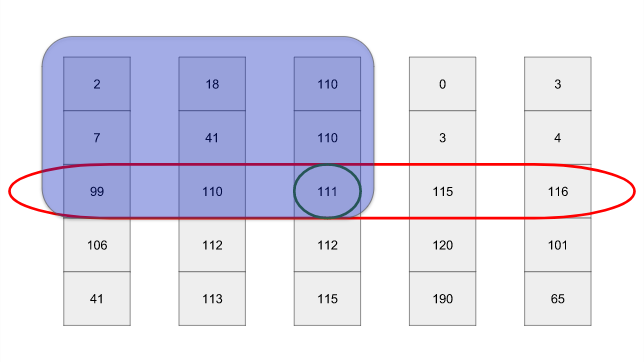
The red oval is the median of the fragments, and the central circle is the median of the medians. Don't forget, we want the pivot to share the list as evenly as possible. In the worst possible case, each element in the blue rectangle (top left) will be less than or equal to pivot. The upper right rectangle contains ³ ⁄ ₅ half lines - 3/5*1/2=3/10 . Therefore, at each stage, we get rid of at least 30% of the rows.

But are we enough to discard 30% of the elements at each stage? At each stage, our algorithm should do the following:

Perform O (n) work on partitioning elements
For recursion, solve one subtask of size ⁷ ⁄ ₁₀ from the original
To calculate the median, the medians solve one subtask the size of ¹ ₅ from the original

As a result, we get the following equation for the total execution time T(n) :

T (n) = T (f r a c n 5) + 7 T (f r a c n 10) + n

$T (n) = T (\ frac {n} {5}) + 7T (\ frac {n} {10}) + n$

It’s not so easy to prove why it is equal to O(n) . A quick solution is to rely on the basic theorem on recurrence relations . We find ourselves in the third case of the theorem, in which work at each level dominates the work of subtasks. In this case, the total work will simply be equal to the work at each level, that is, O(n) .

Summarize

We have quickselect, an algorithm that finds the median for linear time, provided there is a fairly good reference element. We have a median median algorithm, an O(n) algorithm for selecting a reference element (which is good enough for quickselect). Combining them, we got an algorithm for finding the median (or the nth element in the list) in linear time!

Medians for linear time in practice

In the real world it is almost always enough to randomly select a median. Although the median median approach is still executed in linear time, in practice its calculation takes too long. The standard C++ uses an algorithm called introselect , in which the combination heapselect and quickselect is applied; the limit of its execution is O(n log n) . Introselect usually allows using a fast algorithm with a bad upper limit in combination with an algorithm that is slower in practice, but has a good upper limit. Implementations start with a fast algorithm, but return to a slower one if they cannot select efficient support elements.

In conclusion, I will give a comparison of the elements used in each of the implementations. This is not the execution speed, but the total number of elements that the quickselect function considers. It does not take into account the work on the calculation of the median median.

This is what we expected! A deterministic support element almost always considers at quickselect fewer elements than a random one. Sometimes we get lucky and we guess the pivot from the first attempt, which manifests itself as depressions on the green line. Math works!

This can be an interesting use of bitwise sorting (radix sort) if you need to find a median in the list of integers, each of which is less than 2 ³² .
In fact, Python uses Timsort, an impressive combination of theoretical limits and practical speed. Notes on lists in Python .

Source: https://habr.com/ru/post/346930/

All Articles