Frequency method of identification of linear dynamic systems: theory and practice
In practical applications of TAU, it is often necessary to accurately and accurately identify the control object. This article will discuss the identification of the control object by the frequency method. This method is applicable when it is possible to physically test a control object with a sinusoidal input action, changing the frequency over a wide range. If this condition is met, the result, as a rule, justifies the most optimistic expectations.
Let's start with a brief theoretical reference. To understand the material of the article, the reader must have an idea of the following things:
As is known, the response of a dynamic system to a sinusoidal effect is a sinusoid with the same frequency, but with excellent amplitude and phase. It is these two characteristics: the amplitude and phase form the Bode graph, i.e. LAFC and LFCH. In fact, the task of identifying a dynamic system comes down to experimentally finding these two graphs.
For example, consider the equation of a harmonic oscillator with a nonzero right hand side as a sample of a second-order linear dynamical system
Denote the Laplace transform of an arbitrary function through . Apply the Laplace transform to both sides of the equation.
Then the characteristic equation of the dynamical system will be
A transfer function
The desired characteristics of LAFC and LPCHH are obtained by replacing and taking the module and the function argument respectively
Here - amplitude (Magnitude), and - phase (Phase) of the corresponding component at the frequency . The result is something like this.
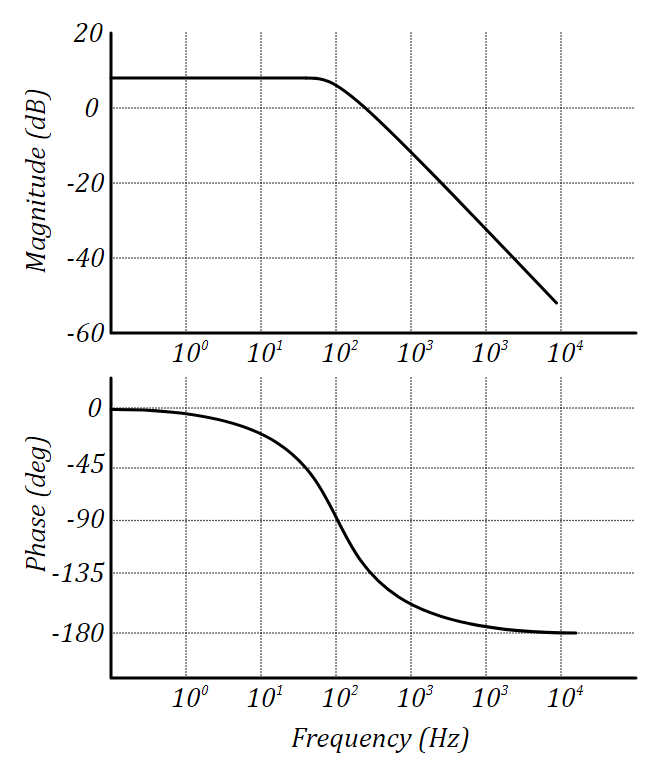
Bode Characteristic: LAFH and LFCH
')
These two graphs unambiguously characterize the dynamic system. The reverse is also true, knowing the LAFC and LPChH of a dynamical system with some accuracy, it is possible to fully identify this system in some confidence intervals. The question is how to get the frequency response. We will tell about it further.
By feeding a sinusoidal effect on the input, we will observe something like this
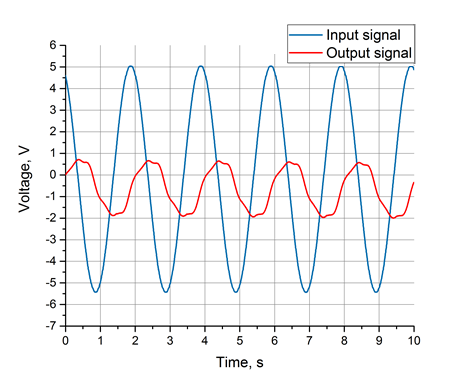
Sinusoidal input and system response
The graph obtained in the experiment. As can be seen from the graph, the output signal clearly has a sinusoidal component with the same frequency as the input signal. However, in addition to this there may also contain higher harmonics and noise. But do not worry, because the Fourier transform is a powerful analytical tool that is so good that it can produce a useful signal, excluding all disturbances.
Let's say we measured two graphs, the input impact and system response for some given frequency of input exposure . It is necessary that both measurements are made synchronously and with the same sampling period. which should be known accurately enough. So we have two sets of discrete values and where , but and - values and at the appropriate discrete points in time . It should be noted that the total measurement time should be large enough to capture at least a few (I would recommend 3 or more) oscillation periods.
To discrete sets and we can apply the discrete Fourier transform. The discrete Fourier transform translates the above signals from the time domain into the frequency domain, that is,
Where , but and - corresponding complex amplitudes th harmonics.
Now apply the discrete Fourier transform to our two signals. The figure below shows amplitude graphs. and
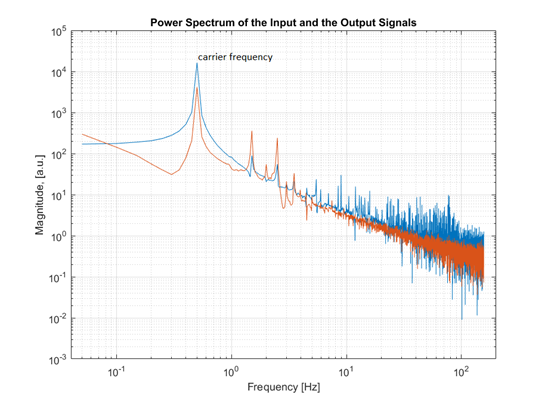
Amplitude spectrum of input and output signal
The graph is also obtained by processing the experimental data. As you can see, there is a sharp peak on the graph at the frequency Hz. This is the "carrier" frequency of the input, that is, the frequency at which the control object was excited. On both graphs, input and output, a peak is observed for this harmonic. Of the two values of the complex amplitudes and at this frequency, we obtain the value of the transfer function .
As we remember
In the case of discrete and we have
Then, we can put a dot on the LAFC and LPFC charts:
What is the frequency of the harmonic with the number ? The answer is: the harmonic frequency is given by the formula
You can also write
The expression for the harmonic itself is the following.
The procedure described above must be repeated enough times to capture the entire frequency range. As a rule, it is possible to use a larger frequency step in the region of low and high frequencies. Conversely, a smaller step is needed in the region of intermediate frequencies, and especially near resonances.
After doing this experiment and processing the data, we obtain a table of frequency characteristics
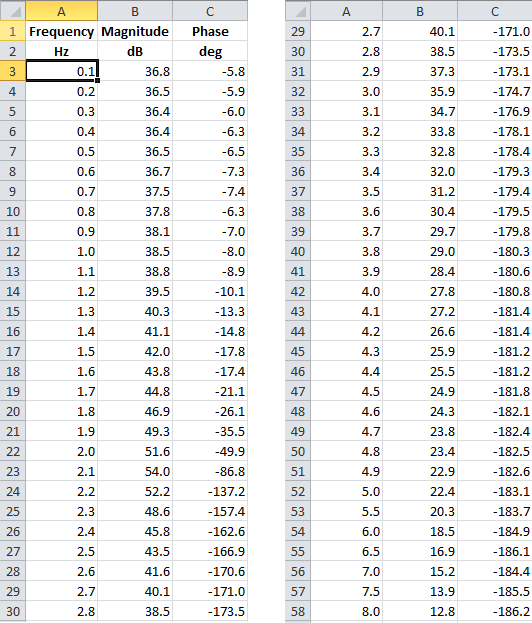
You can immediately build the measured charts LAFC and LFCH. It looks like this

LAFC and LPCHH, built on experimental data
It must be said that, although we used discrete methods, these two graphs reflect the dynamics of the original physical system, that is, the control object, without any simplifications associated with sampling (of course, in this frequency range).
Now you need to use MATLAB, and more specifically System Identification Toolbox. As part of this Toolbox, there is a System Identification App - an interactive application that can identify your system using frequency data. By the way, there are other options, such as identification directly by time measurements.
For correct identification it is necessary to know the order of the system. Here we will help schedule LFCH. To find out the order of the system, look at the LFCh graph and think for how many times the phase at a high frequency lags 90 degrees behind. The number of times at 90 degrees will be the order (denominator) of your system.
During identification, a report is automatically generated, which can be very useful. He looks like this
According to the identification report, the input data is satisfied by the found model at 92.26%. We have the following transfer function of the physical system
Now you have an object of type IDTF with the name tf1, with which you can do everything the same as with any other LTI System in MATLAB. In addition, the object contains information about the uncertainty of internal parameters, and if we build a Bode Plot, then on the graph you can call the display of confidence intervals. In the settings you can specify the number of standard deviations.
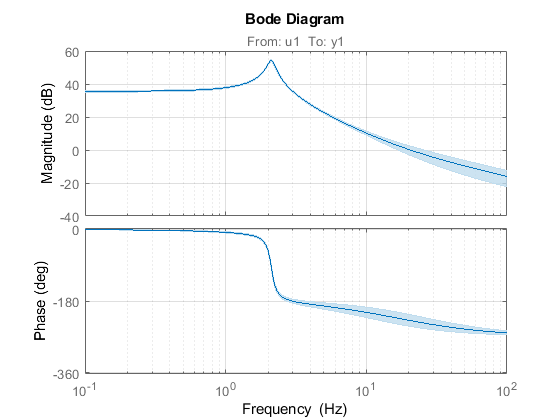
Identified system model with confidence intervals
To verify the identification is correct, you can combine the experimental points with graphs of the frequency characteristics of the identified model
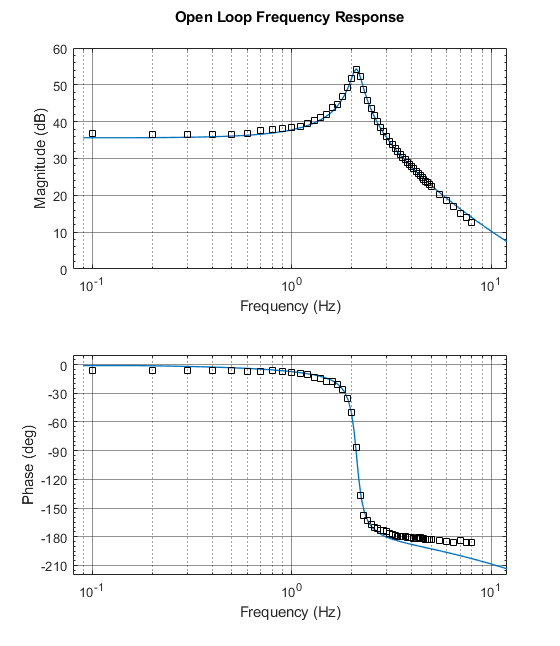
Combined graphics for LAFC and LPFH
Using this method greatly facilitates the process of designing a control system. The author of the article successfully developed and implemented a controller for a special-purpose hydraulic circuit in the LQG hardware. In addition, this method can be used to assess the effectiveness of the control system, provided that you have physically available input effects on the control object from unwanted disturbances.

What you need to know
Let's start with a brief theoretical reference. To understand the material of the article, the reader must have an idea of the following things:
- Laplace Transform
- Linear dynamic systems
- Characteristic equation
- Transmission function
- Discrete Fourier Transform
- Bode Characteristic: LAFH and LFCH
Sinusoidal response
As is known, the response of a dynamic system to a sinusoidal effect is a sinusoid with the same frequency, but with excellent amplitude and phase. It is these two characteristics: the amplitude and phase form the Bode graph, i.e. LAFC and LFCH. In fact, the task of identifying a dynamic system comes down to experimentally finding these two graphs.
For example, consider the equation of a harmonic oscillator with a nonzero right hand side as a sample of a second-order linear dynamical system
Denote the Laplace transform of an arbitrary function through . Apply the Laplace transform to both sides of the equation.
Then the characteristic equation of the dynamical system will be
A transfer function
The desired characteristics of LAFC and LPCHH are obtained by replacing and taking the module and the function argument respectively
Here - amplitude (Magnitude), and - phase (Phase) of the corresponding component at the frequency . The result is something like this.

Bode Characteristic: LAFH and LFCH
')
These two graphs unambiguously characterize the dynamic system. The reverse is also true, knowing the LAFC and LPChH of a dynamical system with some accuracy, it is possible to fully identify this system in some confidence intervals. The question is how to get the frequency response. We will tell about it further.
By feeding a sinusoidal effect on the input, we will observe something like this

Sinusoidal input and system response
The graph obtained in the experiment. As can be seen from the graph, the output signal clearly has a sinusoidal component with the same frequency as the input signal. However, in addition to this there may also contain higher harmonics and noise. But do not worry, because the Fourier transform is a powerful analytical tool that is so good that it can produce a useful signal, excluding all disturbances.
Discrete Fourier Transform
Let's say we measured two graphs, the input impact and system response for some given frequency of input exposure . It is necessary that both measurements are made synchronously and with the same sampling period. which should be known accurately enough. So we have two sets of discrete values and where , but and - values and at the appropriate discrete points in time . It should be noted that the total measurement time should be large enough to capture at least a few (I would recommend 3 or more) oscillation periods.
To discrete sets and we can apply the discrete Fourier transform. The discrete Fourier transform translates the above signals from the time domain into the frequency domain, that is,
Where , but and - corresponding complex amplitudes th harmonics.
Application of the method
Now apply the discrete Fourier transform to our two signals. The figure below shows amplitude graphs. and

Amplitude spectrum of input and output signal
The graph is also obtained by processing the experimental data. As you can see, there is a sharp peak on the graph at the frequency Hz. This is the "carrier" frequency of the input, that is, the frequency at which the control object was excited. On both graphs, input and output, a peak is observed for this harmonic. Of the two values of the complex amplitudes and at this frequency, we obtain the value of the transfer function .
As we remember
In the case of discrete and we have
Then, we can put a dot on the LAFC and LPFC charts:
What is the frequency of the harmonic with the number ? The answer is: the harmonic frequency is given by the formula
You can also write
The expression for the harmonic itself is the following.
The procedure described above must be repeated enough times to capture the entire frequency range. As a rule, it is possible to use a larger frequency step in the region of low and high frequencies. Conversely, a smaller step is needed in the region of intermediate frequencies, and especially near resonances.
After doing this experiment and processing the data, we obtain a table of frequency characteristics

You can immediately build the measured charts LAFC and LFCH. It looks like this

LAFC and LPCHH, built on experimental data
It must be said that, although we used discrete methods, these two graphs reflect the dynamics of the original physical system, that is, the control object, without any simplifications associated with sampling (of course, in this frequency range).
Now you need to use MATLAB, and more specifically System Identification Toolbox. As part of this Toolbox, there is a System Identification App - an interactive application that can identify your system using frequency data. By the way, there are other options, such as identification directly by time measurements.
For correct identification it is necessary to know the order of the system. Here we will help schedule LFCH. To find out the order of the system, look at the LFCh graph and think for how many times the phase at a high frequency lags 90 degrees behind. The number of times at 90 degrees will be the order (denominator) of your system.
During identification, a report is automatically generated, which can be very useful. He looks like this
tf1 = From input "u1" to output "y1": -97.64 s + 1.063e04 --------------------- s^2 + 1.547 s + 176.7 Name: tf1 Continuous-time identified transfer function. Parameterization: Number of poles: 2 Number of zeros: 1 Number of free coefficients: 4 Use "tfdata", "getpvec", "getcov" for parameters and their uncertainties. Status: Estimated using TFEST on frequency response data "h". Fit to estimation data: 92.26% (stability enforced) FPE: 120.6, MSE: 112.3 According to the identification report, the input data is satisfied by the found model at 92.26%. We have the following transfer function of the physical system
Now you have an object of type IDTF with the name tf1, with which you can do everything the same as with any other LTI System in MATLAB. In addition, the object contains information about the uncertainty of internal parameters, and if we build a Bode Plot, then on the graph you can call the display of confidence intervals. In the settings you can specify the number of standard deviations.

Identified system model with confidence intervals
To verify the identification is correct, you can combine the experimental points with graphs of the frequency characteristics of the identified model

Combined graphics for LAFC and LPFH
Conclusion
Using this method greatly facilitates the process of designing a control system. The author of the article successfully developed and implemented a controller for a special-purpose hydraulic circuit in the LQG hardware. In addition, this method can be used to assess the effectiveness of the control system, provided that you have physically available input effects on the control object from unwanted disturbances.
Source: https://habr.com/ru/post/346812/
All Articles