How to train mdl pnmt obratty skrschnya

Recently, I came across a question on Stackoverflow, how to restore the original words from abbreviations: for example, from wtrbtl get a water bottle , and from bsktball - basketball . There was an additional complication in the question: there is no complete dictionary of all possible source words, i.e. the algorithm must be able to come up with new words.

The question intrigued me, and I found it useful to figure out which algorithms and mathematics underlie the modern spell-checkers. It turned out that a good girder can be assembled from an n-gram language model, a word distortion probability model, and a beam search greedy algorithm. The whole construction together is called the noisy channel model.

Armed with this knowledge and Python, in the evening I created a model from scratch, capable of learning the text of "The Lord of the Rings" (!) From scratch to recognize the abbreviations of quite modern sports terms.

Goggles are used a lot where: from the keyboard of your phone to search engines and voice assistants. It is not so easy to make a good girdle, for it must be both quick and ready for everything (including correcting mistakes in words that you have never seen before). That is why so much science is used in the guard. The purpose of the article is to give an idea about this science and just have fun.

Math inside the girdle

The noisy channel model considers each abbreviation as the result of a random distortion of the original phrase.

To restore the original phrase, you need to answer two questions: what source words are likely, and what kind of phrase distortions are likely?

By Bayes theorem,

Where $$$transformation$- this is any such change of the original $$$phrases$which makes it observable $$$abbreviation$. Symbol $$$\ sim$denotes direct proportionality.

And the probability of all sorts of phrases, and the probability of transformations can be estimated using statistical models. I will use the simplest type of model - letter n-grams. It would be possible to apply more complex models (for example, recurrent neural networks), this fundamentally does not change anything.

With such models, you can choose the most plausible source phrase letter by letter using the greedy directional search algorithm, beam search.

N-gram language model

The n-gram model on the previous n-1 letters of the phrase determines the probability of the next, n-th letter (and ignores all the letters that were in front of them). For example, the probability of the letter "g" after the sequence "bowlin" will be calculated by the 4-gram model as $$$p (g | bowlin) = p (g | lin)$because for simplicity, the model ignores all letters preceding these four. Such conditional probabilities are determined (“learned”) by the text corpus. Continuing the example

Where $$$\ # (ling)$ Is the number of "ling" combinations in the learning package, and $$$\ # (lin \ bullet)$ - the number of all 4 grams in the text, starting with "lin".

To evaluate the probabilities of even rare n-grams more adequately, I applied two tricks. First, I add a number to each counter. $$$\ delta$- This ensures that I will not divide by zero. Secondly, I use not only n-grams (which may be few in the text), but also (n-1) -grams (they are more common), and so on, up to the simplest model, which is not looks at the context. But smaller order counters are used with weights decreasing exponentially with the pace $$$\ alpha$. Therefore, the probability $$$p (g | lin)$I calculate how

However, quite a theory! Let's see better how the code of the model looks in Python

from collections import defaultdict, Counter import numpy as np import pandas as pd class LanguageNgramModel: """    ,     .  : order -  (    ),  n-1 smoothing - ,        recursive - ,          : counter_ -   n-,    . vocabulary_ -   ,   """ def __init__(self, order=1, smoothing=1.0, recursive=0.001): self.order = order self.smoothing = smoothing self.recursive = recursive def fit(self, corpus): """       : corpus -  . """ self.counter_ = defaultdict(lambda: Counter()) self.vocabulary_ = set() for i, token in enumerate(corpus[self.order:]): context = corpus[i:(i+self.order)] self.counter_[context][token] += 1 self.vocabulary_.add(token) self.vocabulary_ = sorted(list(self.vocabulary_)) if self.recursive > 0 and self.order > 0: self.child_ = LanguageNgramModel(self.order-1, self.smoothing, self.recursive) self.child_.fit(corpus) def get_counts(self, context): """    ,      : context -   (   self.order ) : freq -    ,   pandas.Series """ if self.order: local = context[-self.order:] else: local = '' freq_dict = self.counter_[local] freq = pd.Series(index=self.vocabulary_) for i, token in enumerate(self.vocabulary_): freq[token] = freq_dict[token] + self.smoothing if self.recursive > 0 and self.order > 0: child_freq = self.child_.get_counts(context) * self.recursive freq += child_freq return freq def predict_proba(self, context): """     ,      : context -   (   self.order ) : freq -    ,   pandas.Series """ counts = self.get_counts(context) return counts / counts.sum() def single_log_proba(self, context, continuation): """       . : context -  ,    continuation -  ,    """ result = 0.0 for token in continuation: result += np.log(self.predict_proba(context)[token]) context += token return result def single_proba(self, context, continuation): """      . : context -  ,    continuation -  ,    """ return np.exp(self.single_log_proba(context, continuation)) 

The "typo" model

A language model was needed to understand what the original phrases are usually. The distortion model is needed to understand how the original phrases are usually distorted.

I will assume that the only possible distortion is the deletion of certain symbols from the phrase. If desired, the model can be modified to take into account other distortions, for example, replacing and rearranging letters.

I do not have a large sample on which to train a complex model. Therefore, to estimate the probability of distortion, I will use 1-gram. That is, my model will simply memorize for each character, with what probability it is deleted from the abbreviation. However, I will encode it just in case in a general form, as an n-gram model.

 class MissingLetterModel: """    ,       : order - ,  n+1 smoothing_missed - ,      smoothing_total - ,      """ def __init__(self, order=0, smoothing_missed=0.3, smoothing_total=1.0): self.order = order self.smoothing_missed = smoothing_missed self.smoothing_total = smoothing_total def fit(self, sentence_pairs): """         : sentence_pairs -   ( , )        . """ self.missed_counter_ = defaultdict(lambda: Counter()) self.total_counter_ = defaultdict(lambda: Counter()) for (original, observed) in sentence_pairs: for i, (original_letter, observed_letter) in enumerate(zip(original[self.order:], observed[self.order:])): context = original[i:(i+self.order)] if observed_letter == '-': self.missed_counter_[context][original_letter] += 1 self.total_counter_[context][original_letter] += 1 def predict_proba(self, context, last_letter): """   ,   last_letter    context""" if self.order: local = context[-self.order:] else: local = '' missed_freq = self.missed_counter_[local][last_letter] + self.smoothing_missed total_freq = self.total_counter_[local][last_letter] + self.smoothing_total return missed_freq / total_freq def single_log_proba(self, context, continuation, actual=None): """    ,   context  continuation   actual  actual  , ,  continuation  . """ if not actual: actual = continuation result = 0.0 for orig_token, act_token in zip(continuation, actual): pp = self.predict_proba(context, orig_token) if act_token != '-': pp = 1 - pp result += np.log(pp) context += orig_token return result def single_proba(self, context, continuation, actual=None): """   ,   context  continuation   actual  actual  , ,  continuation  . """ return np.exp(self.single_log_proba(context, continuation, actual)) 

Model work example

To understand how language models and abbreviations work, let's look at a simple example. We will teach the language model on one word and see how it predicts the continuation of the word "bra". From her point of view, "b" is the most plausible continuation (because this letter most often comes after "a").

 lang_model = LanguageNgramModel(1) lang_model.fit(' abracadabra ') print(lang_model.predict_proba(' bra')) 

  0.181777 a 0.091297 b 0.272529 c 0.181686 d 0.181686 r 0.091025 dtype: float64 

We will also train the model of abbreviations using one example (word, abbreviation). In this example, we have reduced only the letter "a", so for her the model estimates the probability of reduction as high, and for the letter "b" - below. The probability of missing the letter "c" is higher for the model than for "b", because it was less likely to meet the "c" in the training examples.

 missed_model = MissingLetterModel(0) missed_model.fit([('abracadabra', 'abr-cd-br-')]) print({letter: missed_model.predict_proba('abr', letter) for letter in 'abc'}) 

 {'a': 0.7166666666666667, 'b': 0.09999999999999999, 'c': 0.15} 

This is how the abbreviation model assesses the likelihood that abra will be abbreviated as abr-

 print(missed_model.single_proba('', 'abra', 'abr-')) 

 0.164475 

Greedy search for the most plausible phrase

Having models of language and distortion, it is theoretically possible to estimate the probability of any source phrase. To do this, just look at all possible pairs (source phrase, transformation) and evaluate the likelihood of each. But there are too many of them: for example, in an alphabet of 27 characters possible $$$27 ^ {10}$10 letter phrases; to sort them all is unreal. Need a trickier algorithm.

We will use the fact that both models are one-letter, and we will select the letters of the original phrase one by one. To do this, we will get a bunch of incomplete candidate phrases, and for each estimate how much it corresponds to the abbreviation. We will supplement the best candidate with all the various continuation letters and hypotheses about whether they were missed and add to the heap. In order not to create too many options, we will take only "good enough" continuations. Those candidates that may already be full-fledged initial phrases will be set aside, and in the end we will issue as an answer. We will repeat the procedure until the heap ends or the maximum number of iterations.

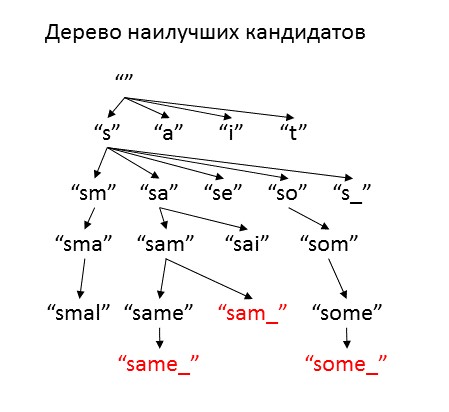
As a measure of the quality of candidates, we will use the estimate of the logarithm of the probability of an existing abbreviation, provided that the original phrase begins as this candidate, and ends as the abbreviation itself. To control the search, we introduce two parameters - optimism and freedom . Optimism estimates how much better the decoding will be when we get to the end of the abbreviation. It makes sense to choose this coefficient between 0 and 1, and the closer it is to 1, the faster the algorithm will try to add new characters to the decryption. Freedom is how much the quality of candidates may be worse than the best current option, and as this parameter increases, the algorithm considers more different options. If you set a very high value of freedom , the algorithm will go through all the options (of which infinity), and work for a very long time, but with small values ​​of freedom, the heap can end before at least one adequate option is found.

 from heapq import heappush, heappop def generate_options(prefix_proba, prefix, suffix, lang_model, missed_model, optimism=0.5, cache=None): """     ( ) : prefix_proba -     prefix -    suffix -     lang_model -   missed_model -    optimism - ,        cache -      :     ( ,  ,   ,  ,     ) """ options = [] for letter in lang_model.vocabulary_ + ['']: if letter: #   ,     next_letter = letter new_suffix = suffix new_prefix = prefix + next_letter proba_missing_state = - np.log(missed_model.predict_proba(prefix, letter)) else: #   ,      next_letter = suffix[0] new_suffix = suffix[1:] new_prefix = prefix + next_letter proba_missing_state = - np.log((1 - missed_model.predict_proba(prefix, next_letter))) proba_next_letter = - np.log(lang_model.single_proba(prefix, next_letter)) if cache: proba_suffix = cache[len(new_suffix)] * optimism else: proba_suffix = - np.log(lang_model.single_proba(new_prefix, new_suffix)) * optimism proba = prefix_proba + proba_next_letter + proba_missing_state + proba_suffix options.append((proba, new_prefix, new_suffix, letter, proba_suffix)) return options 

If you read my code carefully, you will notice that I made another simplification - instead of summarizing the probabilities of all the distortions of the original word, I consider only one distortion. This is not always true: for example, "ball" can be abbreviated to "bl" by deleting both the first ("b - l") and the second ("bl-") letter "l". But if there are no such repetitions, an adequate reduction option is almost always the only one.

 def noisy_channel(word, lang_model, missed_model, freedom=3.0, max_attempts=10000, optimism=0.9, verbose=False): """  ,     word : word -  lang_model -   missed_model -    freedom -        max_attempts -   optimism - ,        verbose -          :    -    -    .   ,   . """ query = word + ' ' prefix = ' ' prefix_proba = 0.0 suffix = query full_origin_logprob = -lang_model.single_log_proba(prefix, query) no_missing_logprob = -missed_model.single_log_proba(prefix, query) best_logprob = full_origin_logprob + no_missing_logprob #      heap = [(best_logprob * optimism, prefix, suffix, '', best_logprob * optimism)] #       -    candidates = [(best_logprob, prefix + query, '', None, 0.0)] if verbose: print('baseline score is', best_logprob) #      cache = {} for i in range(len(query)+1): future_suffix = query[:i] cache[len(future_suffix)] = -lang_model.single_log_proba('', future_suffix) # rough approximation cache[len(future_suffix)] += -missed_model.single_log_proba('', future_suffix) # at least add missingness for i in range(max_attempts): if not heap: break next_best = heappop(heap) if verbose: print(next_best) if next_best[2] == '': #     #    ,     if next_best[0] <= best_logprob + freedom: candidates.append(next_best) #     if next_best[0] < best_logprob: best_logprob = next_best[0] else: # it is not a leaf - generate more options prefix_proba = next_best[0] - next_best[4] # all proba estimate minus suffix prefix = next_best[1] suffix = next_best[2] new_options = generate_options(prefix_proba, prefix, suffix, lang_model, missed_model, optimism, cache) # add only the solution potentioally no worse than the best + freedom for new_option in new_options: if new_option[0] < best_logprob + freedom: heappush(heap, new_option) if verbose: print('heap size is', len(heap), 'after', i, 'iterations') result = {} for candidate in candidates: if candidate[0] <= best_logprob + freedom: result[candidate[1][1:-1]] = candidate[0] return result 

We apply our algorithm to search for possible decoding of the abbreviation "brc".

 result = noisy_channel('brc', lang_model, missed_model, verbose=True, freedom=1) print(result) 

 baseline score is 7.68318306228 (6.9148647560475442, ' ', 'brc ', '', 6.9148647560475442) (6.755450684372974, ' b', 'rc ', '', 4.7044649199466617) (5.8249119494605051, ' br', 'c ', '', 2.6863637325526679) (7.088440394887126, ' brc', ' ', '', 1.7075575253192956) (7.1392598304831516, ' bra', 'c ', 'a', 2.6863637325526679) (7.6831830622750497, ' brc ', '', '', -0.0) (8.0284469273601662, ' brac', ' ', '', 1.7075575253192956) (8.3621576081202385, ' a', 'brc ', 'a', 6.776535093383159) (7.6954572168460142, ' ab', 'rc ', '', 4.7044649199466617) (6.7649184819335453, ' abr', 'c ', '', 2.6863637325526679) (8.0284469273601662, ' abrc', ' ', '', 1.7075575253192956) (8.0792663629561936, ' abra', 'c ', 'a', 2.6863637325526679) (8.6231895947480908, ' abrc ', '', '', -0.0) (8.6231895947480908, ' brac ', '', '', -0.0) (8.6740629096242063, ' brca', ' ', 'a', 1.7075575253192956) heap size is 0 after 15 iterations {'brc': 7.6831830622750497, 'abrc': 8.6231895947480908, 'brac': 8.6231895947480908} 

Testing for hobbits

You can truly test written algorithms only with a good language model. I was wondering how qualitatively the model would be able to decipher abbreviations, having studied on a deliberately limited corpus - one book, and even a specific subject. The first book that came to my hand is "The Lord Of The Rings: The Fellowship Of The Ring". Well, let's see how the Hobbit language can help decipher modern sports terms.

For starters, the code for learning the model

 import re #   with open('Fellowship_of_the_Ring.txt', encoding = 'utf-8') as f: text = f.read() #        text2 = re.sub(r'[^az ]+', '', text.lower().replace('\n', ' ')) all_letters = ''.join(list(sorted(list(set(text2))))) print(repr(all_letters)) # ' abcdefghijklmnopqrstuvwxyz' #      : missing_set = ( [(all_letters, '-' * len(all_letters))] * 3 #      + [(all_letters, all_letters)] * 10 #       + [('aeiouy', '------')] * 30 #      ) #    big_lang_m = LanguageNgramModel(order=4, smoothing=0.001, recursive=0.01) big_lang_m.fit(text2) big_err_m = MissingLetterModel(order=0, smoothing_missed=0.1) big_err_m.fit(missing_set) 

 ' abcdefghijklmnopqrstuvwxyz' 

I chose the four-gram model of the language by comparing the plausibility of different models on the “test sample” at the very end of the book. It turned out that the quality of predicting the probability of letters increases with the growth of the model order to 4. I did not use even greater order, because with the growth of the order, the speed of the model decreases greatly.

 for i in range(5): tmp = LanguageNgramModel(i, 0.001, 0.01) tmp.fit(text2[0:-5000]) print(i, tmp.single_log_proba(' ', text2[-5000:])) 

 0 -13858.8600648 1 -11608.8867664 2 -9235.21749986 3 -7461.78935696 4 -6597.9544372 

Let's apply our algorithm to different abbreviations. Sam, I thought of, for example, recognized the model without difficulty, and also added other options (however, with a higher speed, and therefore less believable).

 noisy_channel('sm', big_lang_m, big_err_m) 

 {'sam': 7.3438449620080997, 'same': 9.5091694602417469, 'some': 7.6890573935288824} 

Frodo is also recognized without problems.

 noisy_channel('frd', big_lang_m, big_err_m) 

 {'frodo': 6.8904938902680888} 

The ring is uniquely guessed.

 noisy_channel('rng', big_lang_m, big_err_m) 

 {'ring': 7.6317120419343913} 

Before running "wtrbtl", check the decryption in parts. With water, everything is fine.

 noisy_channel('wtr', big_lang_m, big_err_m) 

 {'water': 8.6405279255413898} 

The bottle is not so confidently recognized by the model. Still, the battle in "The Lord of the Rings" are often referred to as bottles.

 noisy_channel('btl', big_lang_m, big_err_m) 

 {'battle': 12.620490427990008, 'bottle': 13.3327872548629, 'but all': 14.66815480120338, 'but ill': 15.387630853411283} 

For example, in the following phrases:

 noisy_channel('batlhrse', big_lang_m, big_err_m) 

 {'battle horse': 25.194823785457018, 'battle horses': 27.40528952535044} 

There are a lot of alternatives for a bottle of water:

 noisy_channel('wtrbtl', big_lang_m, big_err_m) 

 {'water battle': 23.76999162985074, 'water bottle': 23.962598992336815, 'water but all': 24.445047133561353, 'water but ill': 25.164523185769259, 'water but lay': 25.601336188357113, 'water but lie': 26.668305553728047} 

But the basketball (never seen) model recognized almost correctly, since the word "basket" was used in the training text. But in order to do this, we had to manually increase the width of the "beam" from which the model chooses options.

 print(noisy_channel('bsktball', big_lang_m, big_err_m, freedom=5)) 

 {'bsktball': 33.193085889457429, 'basket ball': 33.985227947093364} 

But the word "ball" in the training text did not occur once, and the model did not restore it on its own (but Bilbo was suspected of the name in "bl"). The word "bowling" in the "Lord of the Rings" also never met, but based on some general idea of ​​the language, the model still suggested it.

 print(noisy_channel('bwlingbl', big_lang_m, big_err_m, freedom=5)) 

 {'bwling blue': 31.318936077746862, 'bwling bilbo': 30.695249686758611, 'bwling ble': 34.490254059547475, 'bwling black': 31.980325659562851, 'bwling blow': 33.15061216480305, 'bewilling blue': 30.937989778499748, 'bewilling bilbo': 30.314303387511497, 'bewilling ble': 34.109307760300361, 'bewilling black': 31.599379360315737, 'bewilling blin': 34.685939493896406, 'bewilling blow': 32.769665865555929, 'bewilling bill': 32.156071732628014, 'bewilling below': 32.195518180732158, 'bwling bill': 32.537018031875135, 'bewilling belia': 32.550377929021479, 'bwling below': 32.576464479979279, 'bwling belia': 32.931324228268608, 'bwling belt': 33.203704016765826, 'bwling bling': 33.393527121566656, 'bwling bell': 34.180762531759534, 'bowling blue': 30.676613106535022, 'bowling bilbo': 30.052926715546771, 'bowling ble': 33.847931088335635, 'bowling black': 31.338002688351011, 'bowling blin': 34.42456282193168, 'bowling blow': 32.508289193591203, 'bowling bill': 31.894695060663285, 'bowling below': 31.934141508767446, 'bowling bl': 34.983414721126472, 'bowling blad': 34.992926061009179, 'bowling belia': 32.289001257056761, 'bwling blind': 35.000922570770712} 

Generate uporotyh texts

In the end, in order to cheer you up a bit, I tried to turn the piece of the “Lord of the Rings” text itself into cuts. It turned out strange.

 part = text[10502:11149] result = '' for i, letter in enumerate(part): if np.random.rand() * 0.5 < big_err_m.single_proba(part[0:i], letter): result += letter print(result) 

 This bok s largly cncernd wth Hbbts, nd frm its pges readr ma dscver much f thir charctr nd littl f thir hstr. Furthr nfrmaton will als b fond n the selction from the Red Bok f Wstmarch that hs already ben publishd, ndr th ttle of The Hobbit. Tht stor was dervd from the arlir chpters of the Red Bok, cmpsed by Blbo hmslf, th first Hobbit t bcome famos n the world at large, nd clld b him There and Bck Again, sinc thy tld f his journey into th East and his return: n dvntr whch latr nvolved all the Hobbits n th grat vnts of that Ag that re hr rlatd. 

The linguistic model can be used to generate text "in Tolkien's style", though without any sense.

 np.random.seed(20) text = "Frodo" for i in range(300): proba = big_lang_m.predict_proba(text) text += np.random.choice(proba.index, size=1, p=proba)[0] print(text+'.') 

 Frodo would me but them but his slipped in he see said pippin silent the names for follow as days are or the hobbits rever any forward spoke ened with and many when idle off they hand we cried plunged they lit a simply attack struggled itself it for in a what it was barrow the will the ears what all grow. 

The science of data has not yet learned to generate "from scratch" connected texts. For this, we need a real artificial intelligence, possessing an understanding of the plot that unfolded once in Middle-earth.

Conclusion

Natural language processing is actually a very complex blend of science, technology, and magic. Even linguistic scholars do not fully understand the laws according to which speech is arranged. And until the time when the machines will be able to understand the texts in the full sense of the word, it’s not very soon.

Natural language processing is also fun. Armed with a pair of statistical models, it turns out, you can both recognize and generate unobvious abbreviations. For those who want to continue my entertainment, here is the complete experiment code.

But if you replace the n-gram model with a recurrent neural network, you can generate texts of a higher degree of connectivity (and even almost compiled code). In the near future I will try to generate a typical Habr-style neuron article (which I have already submitted ), so subscribe and wait :)