Richard Hamming: Chapter 23. Mathematics

Hi, Habr. Remember the awesome article "You and your work" (+219, 2194 bookmarks, 345k reads)?

So Hamming (yes, yes, self-checking and self-correcting Hamming codes ) has a whole book based on his lectures. Let's translate it, because the man is talking.

This book is not just about IT, it is a book about the thinking style of incredibly cool people. “This is not just a charge of positive thinking; it describes the conditions that increase the chances of doing a great job. ”
')
We have already translated 5 chapters.

Chapter 23. Mathematics

(For the translation, thanks to Jerry OK, who responded to my call in the previous chapter. ") Who wants to help with the translation - write in a personal or mail magisterludi2016@yandex.ru

In life, our attention is mainly chained to things in the foreground, and the world around us is taken for granted. We take for granted air, water, and many other things, such as language and math. When you work in a company for a long time, its structure, methods and customs are also taken for granted.

It is worthwhile to look closely at such usual things that did not attract your attention from time to time, since big steps forward often occur due to such actions, and rarely without them. For this reason, we will look at mathematics, although the same consideration of language can also be fruitful. We use mathematics without even discussing what it is. Most of us never really thought about it, we just did mathematics - but it is she who plays the main role in science and engineering.

Perhaps the “favorite” definition of it, given by mathematicians themselves, is:

“Mathematics is what is done by mathematicians, and mathematicians are those who do mathematics.”

Such a definition not only gives rise to jokes, but is also an honest admission that scientists themselves do not believe that mathematics can be adequately defined. There is a well-known book “What is Mathematics”, the authors of which consider mathematics from all sides, but do not try to define it.

Once at a cocktail party, the head of the mathematical department of Bell Labs said to a young girl three times:

"Mathematics is nothing but pure thinking."

I doubt that the interlocutor agreed, but in the end she changed the subject; it impressed me. You can also say:

"Mathematics is nothing but the language of pure thinking."

This does not mean that mathematics is flawless - not at all - but it seems that we have nothing better. Just look at people involved in law or tax calculation, and how they use natural language to express their thoughts, to see how bad it is for pure thinking. Why, the simple statement “I lie” is already contradicting itself!

There are many natural languages ​​in the world, but there is only one language of mathematics. Indeed, there is the Roman numeral “VII”, the Arabic “7” (of course, in Latin, not Arabic), the binary record “111”, but they all mean the same thought in different representations. Seven is seven, and in any record this is a prime number. Seven as a number should not be confused with his record.

Most people, seriously thinking about the possibility of extraterrestrial contact, agree that if we ever contact the civilization of a distant star, then its inhabitants will have essentially the same mathematics as ours. The words “essentially the same” are necessary here, because, for example, their Euclidean geometry may include orientation, because of which for them two triangles may be congruent or anti-congruent (see figure). Similarly, Ptolemy, arguing about astronomy in his "Almagest", used the designation "sin x" where we would use "2 * sin (x / 2)" (see figure) - in essence, the idea remains the same. Note that from the assumption of a connection with them, it follows that they should evolve to the level at which they know the Maxwell equations in one form or another. However, I should note that some philosophers even doubt that the communication system of another civilization will be at least something similar to ours. But people constantly hovering in the clouds can imagine anything, and this will very rarely be close to the truth (an example of this is the argument about the possible presence of a multimeter layer of dust on the lunar surface in which the spacecraft will sink and people will suffocate).

Over the years, five basic schools have been developed, which define mathematics in their own way, and none of the definitions is complete.

The oldest of these schools is Plato. Perhaps it is precisely her views that most mathematicians hold when they don’t think about it. Plato (427-347 BC) argued that the idea of ​​a chair is more real than any individual chair. Material chairs wear, scrape, collapse and lose; the ideal chair is immutable, eternal - as he said. Therefore, he argued, the world of ideas is more real than the material world. The theorems of mathematics and its other components belong to the world of ideas (as Plato asserted). Along with the number 7 mentioned above, they are not found in the material world. You never saw, did not hear, did not touch and did not try abstract number 7. Yes, you saw 7 horses, 7 cows, 7 chairs, but not number 7 — pure 7, not polluted by a concrete implementation.

The metaphor Plato used was that we see reality only through the shadows she casts on the wall. Real reality cannot be seen, only its shadows reach our senses. According to Plato, our mind is that which overcomes this limitation and achieves real ideas.

That is why Platonist mathematicians say that they "discovered" the result, and not "created" it. If I am a Platonist, then I “discovered” codes correcting errors, and not “created” them. Results were always available and waited for them to be opened.

The problem with Platonism is that it is not very plausible and definitely cannot explain how mathematics develops, without taking into account its development and development. The basic ideas and definitions of mathematics gradually changed over the centuries, and this is inconsistent with the idea of ​​unchanging Platonic ideas. Euler’s (1703-1783) continuity concept is quite different from the one you were taught. Of course, it can be argued that the changes come from the fact that we manage to “see” ideas in more detail over time. But let us recall the non-Euclidean geometry, which arose only because of the intervention in the postulate of parallel straight lines, and think of many other potential geometries that must exist in the Platonic world. All possible mathematical ideas and all consequences derived from them must exist in this world throughout eternity! All of them must exist from the time of the Big Bang!

The second primary school of mathematicians is the formalists. For them, mathematics is a formal game that begins with a set of lines of abstract characters and consists in performing allowed transformations on lines in the same way as in algebra. For formalists, mathematics is a purely mechanical game, where the interpretation of symbols is not allowed, which does not allow you to make purely human errors. The founder of the formalism is David Gilbert. This approach to mathematics is popular among people working in the field of artificial intelligence, because such operations are mostly done by machines.



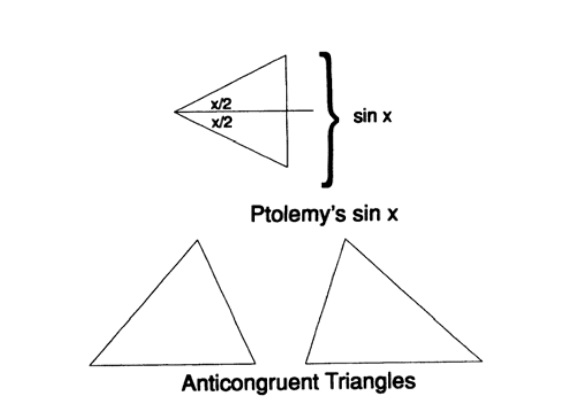
Fig. 1: Possible differences in the understanding of mathematics



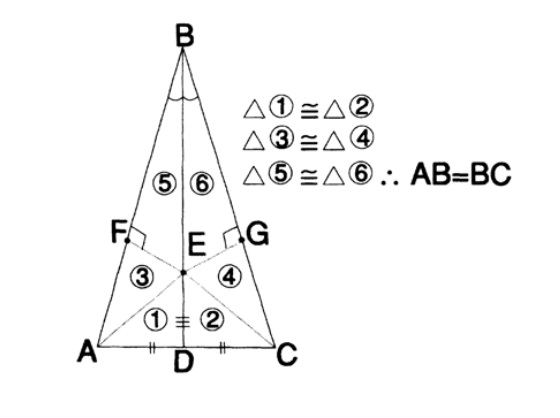
Fig. 2: Proof of the isoscience of an arbitrary triangle

There is a well-known from the end of the Middle Ages (although I never found out where it was discovered for the first time) the well-known proof of the isosity of any triangle using classical Euclidean geometry.

Let's start with the triangle ABC (see figure). We draw the bisector from point B and the height from point D (mid AC); these lines intersect at point E. From it, we lower the perpendiculars to AB and BC. The upper two triangles will be equal in two angles and the common side between them, the lower two - in equal legs. Then the remaining triangles will also be equal on both sides and the angle between them. From all this it follows that AB = BC, and the original triangle is isosceles. Obviously, the proof of the theorem is erroneous, but it corresponds to the style of the classical Euclidean geometers, so that there is initially some kind of error. Note that with the help of metamathematical reasoning we came to the conclusion that the mathematical calculations led us to the erroneous conclusion!

To show what made the erroneous conclusion (and other possible errors), Hilbert studied what Euclid did not describe in his writings - the concept of location between two points (intersection) and intersection. With this, Hilbert was able to prove that the intersection of the lines shown occurs outside the triangle, and not inside it, as shown in the drawing. In the process, he introduced many more postulates than Euclid described!

I was a mathematics graduate student when this caught my attention. I read a little on this topic and thought hard. As far as I know, Euclid has about 467 theorems, but none of them became false after Hilbert added his postulates. However, each theorem that needed new postulates could not be strictly proved by Euclid! Every theorem that followed from such theorems and was based on them was also not proved by Euclid. But the results in the expanded system remained the same as Euclid expected. How could it happen that Euclid, despite the fact that he did not prove a significant part of his theorems, was never mistaken? Luck? Hardly!

It soon became obvious to me that not a single theorem was refuted because Hilbert “knew” that Euclidean theorems were “correct” and picked up additional postulates so that they were consistent with the theorems. But then I realized that Euclid was in the same position: he considered the Pythagorean theorem to be true, like many others, and had to find a system of postulates that would ultimately give the result known to him in advance. Euclid did not set out the postulates and made conclusions from them, as is usually stated; He paved the way from "known" results to the postulates he needed!

Paraphrasing one of Hilbert's assertions, "when severity comes, meaning goes away . "

Formalists argue that there is no “meaning” in mathematics — but if so, then why should society support mathematics and mathematicians? Why was mathematics so useful? If there is no point in mathematics anywhere, then why do its postulates and definitions change over time? Formalists simply cannot explain why mathematics is more than an idle game like the movement of pieces on a chessboard.

The school of logicism is closely associated with formalism, the followers of which tried to bring all the mathematics into the section of logic. They, like many others, failed to complete their task - and for them it is more painful than others, because they are logicians! The famous attempt of Russell and Whitehead, the three-volume Principia Mathematica, was generally abandoned, despite the fact that a significant part of their work remained valid. Let's quote Russell's famous quote:

“Pure mathematics consists entirely of assumptions, meaning that if one statement is true, then the other statement is also true in a specific case. It is essential not to discuss whether the first statement is true and what the circumstances are in which the second is true. ”

Here you can see the mix of approaches of logicists and formalists and the purity of their views. Logicists failed to convince people that their approach is not just an exercise in logic. In fact, I say: what is considered the foundation of mathematics, in fact, is only a superstructure. A simple example that I cite over the years: if you go to my office and prove that the Cauchy theorem is false, that is, it is not fulfilled from the usual assumptions, then I will definitely be interested, but in the end I will ask you to return with new prerequisites - I “I know” that the Cauchy theorem is “true.” Thus, at least for me, mathematics does not follow solely from the premises; chatter, very often the premises follow from the theorems, which we consider "true". I am inclined, like many others, to combine formalists and logisticists.

Definitely, mathematics is not reduced to the formulation of postulates and strict deductions from them, as the formalists present. Indeed, almost every graduate student mathematician felt that they had to correct the evidence of the early great mathematicians, and somehow the theorems did not change much, despite the fact that their authors did not actually prove the modified theorems. True (although this is rarely mentioned), the definitions in mathematics, as a rule, gradually change with time, which is why previous proofs can no longer be applied to the same provisions of the theorem - we now understand its meaning a little differently.

The fourth school is intuitionists who uniquely solve the “severity-sense” dilemma, ignoring severity. If you need absolute rigor, then since we have an ever-increasing standard of rigor, presumably, none of the “proved” theorems have actually been proven. Rather, the next generation will be forced to correct our results, which means that we will not prove anything!

If you want to know, I'm partly an intuitionist. The example given about the Cauchy theorem illustrates my position: mathematics should do what I want from it. Unlike Hermite (1822-1901), who said: “We are not masters, but servants of mathematics,” I tend to think (from time to time) that we are masters. The postulates of mathematics were not on the tablets that Moses brought from Mount Sinai; they are created by people and therefore can change as we please. Neither my opinion, nor Hermite’s view are absolutely true, the truth is somewhere in the middle: we are both masters and servants of mathematics.

The nature of language inclines us to yes-no answers: there is something or no, you either have proof or not. But as soon as we recognize that there is a changing standard of rigor, we are forced to admit that some of the evidence is more convincing than others. If we evaluate the evidence on a scale from 0 to 1, as for probability, then they will all be inside this interval and, most likely, never reach the upper limit of 1 - certainty.

The last primary school is constructivism. His followers insist that you have to provide methods for constructing everything that you are talking about. For them, the approach of the formalists is unacceptable, who believe that if the set of postulates is not considered contradictory, then the objects defined by them “exist”. The constructivist approach can cause many problems. None of the other four schools provides a strict basis for mathematics, but the views of the constructivists are too strict, since they exclude too much of what is valuable for us in practice. Informatics specialists, with the exception of those working with artificial intelligence, usually consider themselves to be constructivists, if they think about it at all.

In fact, some experts in numerical analysis believe that the system of real (real) numbers is the bit sequences in a computer, that is, they are really real. Therefore, it is argued that "imaginary" numbers are truly imaginary. But for most users, mathematics is simply a tool that does not need to be understood.

There is a group of people working with software who believe that we must “prove the correctness of programs” just as we prove the correctness of mathematical theorems. They make two mistakes:

1. In fact, we do not "prove" the theorem!
2. Many important programming problems cannot be formulated so precisely that they can be proved, rather, the emerging program defines the problem!

This does not mean that there is nothing valuable in their approach to proving the correctness of programs, only, as often happens, their claims are greatly exaggerated. Most scientists, doing math day after day, consider themselves to be a Platonic school. But if you get them to answer the question of exactly what their job is, they usually take refuge in formalism, arguing that mathematics is an idle game with meaningless characters (not that they believed in it, but it is a convenient defensive position) . They pretend to believe in Russell’s quoted quote.

As you know from your math course, what you really do if you look at the philosophical level is almost never mentioned. Professors are too busy with the details of mathematics to discuss even exactly what they are doing - the typical behavior of a techie!

However, as you know, mathematics is extremely useful in this world, and we use it without even thinking about it. Let's take a look at this in more detail. The ancient Greeks believed that mathematics is true. There was practically no doubt about it. What could be more true than 1 + 1 = 2? But remember, when we discussed codes for correcting errors, we said that 1 + 1 = 0. These different ways of using the same characters (you can argue that the units in these two statements are not the same, if you will) are contrary to logic. Perhaps, for the first time, mathematicians came face to face with the fact that there could be other systems of mathematics when the first non-Euclidean geometries appeared. They use the same words, such as "point", "line", "plane", but, obviously, their meanings are different. This should not surprise you; when you studied forces in mechanics, you had to realize that scalar addition for vectors is not applicable. And the word "work" in physics means not the same thing that we usually mean.
in everyday life.

The mathematics you choose to use comes from the application; it is not universal and "true." Then how should we choose the appropriate math for various tasks? What is the meaning of mathematical symbols? Careful consideration of the question suggests that the “value” of the symbol comes from how it is used, and from the definitions, as Euclid (and you) thought, defining points, lines and planes. Now we understand that his definitions are ambiguous and do not define anything uniquely; meaning comes from the relationship between characters. This is similar to the interpreted language, the outline of which I cited in Chapter 4: the value of the instruction is contained in the subroutine it calls — in how the character is processed, not in its name! The characters themselves are just bit strings in the car, and without knowing how they will be processed, they do not carry a meaning in themselves.

Mathematician Dodgson (Lewis Carroll), who wrote “Alice in Wonderland” and “Alice in Wonderland”, specialized in logic, and these two books are graphic illustrations of how the meaning is determined by use. Therefore, Humpty Dumpty said: “When I take a word, it means what I want, no more and no less”; Alice thought that words made sense regardless of their context, and they could not be used arbitrarily.

At this point, it should be clear that the symbols have the meaning that we assign to them. We are all familiar with different natural languages, where synonymous words indicate the same object. Returning to Plato; what is the chair? Is it always the same idea, or does it depend on the context? At a picnic, a cobblestone can be a chair, but you do not expect someone to use a cobblestone as a chair in your bedroom. , : , , — , .

As a result, you may ask yourself: how does a child learn a language? It is one thing to learn a second language, knowing the first, but learning the first language is another thing, because it is not clear where the meaning should arise. You can use gestures for nouns and verbs a little, but many words are not so obvious. When I point to a horse and say “horse,” do I mean the name of this particular horse, all horses, four-legged, mammals, living creatures? Or maybe we are talking about the color of this horse? How should the other person know what meaning is meant in a particular situation? In fact, how does a child learn to distinguish between a separate horse and a more abstract class of horses?

Apparently, as I said earlier, the meaning arises when using the word, otherwise it is not defined. Several years ago, the authors of the famous dictionary admitted that they are not able to strictly prescribe the use of words. They can only say how words are used. The authors of the dictionary had to be "descriptive," not "prescriptive." The fact that there is no absolute, correct meaning for each word has angered many. For example, both the New Yorker book reviewer and the hero of detective novels, Nero Wolfe, were angry with the new vocabulary. Now we see that all the "truth" that must be inherent in mathematics is a mirage. All this is arbitrary, human agreements.

. , «», «», , , , .

, , — ! , . — - .

The fundamental paradox of life described by Einstein is that the world looks logically constructed. Here is the most amazing thing - the world can be known logically and mathematically. I must warn, however, that recent research in fundamental physics makes one doubt what has been said, and this is discussed in the next chapter.

, , «». , . 0 1 ( 0 1, ), «» , 1+1=0 : — , . , .

, , , , , , .

. , . , , , .

( ) — . . -, , , , «» . , , , , — , , , , , . , , . , , , !

I want to end on an even more provocative note. It is not obvious - although many people, beginning with the ancient Greeks, act as if it is true - that all things, whatever they may be, can be expressed in words. You can discuss anything you want: gods, truth, beauty, justice. But if we imagine a musical concert, it will become clear that what is transmitted to the audience cannot be expressed in words - if this were possible, the composer and the musicians could use them. Unlike music criticism, transmitted by music cannot (apparently) be embedded in words. The same, but to a lesser extent, is true for painting. Poetry is an interesting case: it uses words, but the real meaning is not in them!

Likewise, the three pillars of ancient Greece, truth, beauty, and justice, cannot be expressed in words, although we believe that they mean. Since the days of Hammurabi (1955-1913 BC) an attempt to express justice with words produces the law, and it usually does not coincide with your understanding of justice. In the Bible there is the famous question “What is truth?”. And who, besides the judge of a beauty contest, dares to define “beauty”?

, , , , , ( , , ) , 7? , , . .

. , ( ), , , . , «tall» («»/«»/«») «tall building», «tall person», «tall tale» . , , , . , , , , , , , , . , , , .

( ) , , , . 19, , .

, , , . , . , , . , , .

, , !

To be continued...

Who wants to help with the translation - write in a personal or mail magisterludi2016@yandex.ru