Just about the graphs. Attempt to popularize

"Any titles (nobleman, merchant, tradesman, peasant, etc., titles - princely, earl, etc.) and the name of civilian officials (secret, state, etc. advisers) are destroyed ..."

On the destruction of estates and civilian ranks
Decree of the All-Russian Central Executive Committee and Sovarka on November 10, 1917, art. 2

---

Somehow I did without it before ...

Is there any benefit to an ordinary programmer or, say, a philistine from graph theory, or is this a purely sacral thing, from arrogant mathematical abstractions?

Probably, the specificity of “ randomly distributed graphs ” will not have much demand in our everyday life, but some idea of ​​graph theory may be useful in a wide variety of situations, even to a person not particularly well-placed in mathematics — as for people working in a field like programming then the sophisticated inventiveness, as a rule, accompanies the tasks that fall daily to their share, therefore the representatives of this profession, in search of new ideas and tools, happen to be recklessly busy Thinking their mind with things that would not seem useful, however, having ordered pizza for 10 thousand bitcoins , they give a good mood to other good people for many years, and still justify their drive.

Well, let us suppose we rank ourselves as quite serious people and intend to quite seriously turn ourselves to the use of a small amount of knowledge that we find difficult to accumulate and, over the years, with increasing labor, we keep it in our head. And we firmly reject the luxury of negligent oblivion of information once received by us.

A graph can be an excellent means of visualizing your ideas. Every day we solve any tasks that can be adequately written in the language of graphs, but often do not feel the need to manipulate visual images. Sometimes it is the visual image that has the necessary effect on our mental concentration, which leads us to a bright idea. - Often it is useful to look at things from different angles.
')
The graph may be the expression of the essence of some idea and shorten your path to the final goal (if you now think about the sad, then I did not mean it).
It often happens that we use unconsciously, intuitively, some techniques for solving problems that arise before us, which are the essence of user patterns suggested by previous experience, and meanwhile, these techniques, cast into an idea, built into a paradigm, turned into a concept, can become powerful a tool that tells us both the direction and the way to solve a whole class of problems united by a common feature.

Graph theory currently contains quite a few effective tools for solving an equally wide range of problems. However, the means and ideas that today belong to the field of discrete mathematics , called graph theory , remain, to this moment, in some kind of eclectic unity, as it were, not without forcible compulsion. The range of issues solved by the theory of graphs, and the variety of models and mechanisms for solving them, are so extensive that attempts to popularize graph theory as a whole must be based on a considerable boldness. The academic and in-depth presentation of the specific nuances of graph theory will not be the goal of this article. We intend to speak only about what we have found useful (or relatively useful) and non-boring use.

And by the way, “how is it going” graph theory?

We pay tribute to the great names and briefly turn to historical retrospectives.

... This is a decision in nature; apparently, has little to do with mathematics, and I don’t understand why one should rather expect this decision from a mathematician than from some other person, because this decision is supported only by reasoning and there is no need to involve any laws to find this solution peculiar to mathematics.

From a letter from Leonard Euler to his friend Karl Gottlieb Eleler, 03 [14] April 1736 ^{[ 1 ]}



Fig. 1. Konigsberg on an engraving of the 17th century.

It is believed that graph theory began to take shape as an independent mathematical discipline after Euler’s exponential solution to the “ seven bridges problem ”, a purely logistic problem, and the application of graph theory to solving the four-color dice problem required, in my opinion, much more ingenuity and great sophistication in the subject, achieved only by constant exercises in the practical application of graph theory, although by the time the last of the mentioned problems was solved, more than two centuries, and the subject of a new discipline, a vague vision of Euler, managed to acquire the outlines very specific and gain some experience of the practical application of the efforts of outstanding scientists who developed the idea of ​​Euler.

[Fig. 1 can give some insight into the “task” mentioned in the quoted phrase.] In 1736, part of the urban communication and architectural ensemble of the city of Königsberg were 7 bridges (these old bridges were not preserved) across the River Pregel. It is difficult to say how widespread the riddle was about whether it was possible to cross all seven bridges without going through any of them twice , and whether city services seriously thought about establishing such a route for city guests and citizens, but this mystery managed to attract attention Leonhard Euler - however, remained for quite a long time the only known example of the application of the method proposed by the great mathematician. For more than a hundred years, Euler’s work did not arouse much interest in the academic community. The term “count” was introduced by the Hungarian mathematician Denish Koenig only in 1936.

I was once offered the task of an island located in the city of Königsberg and surrounded by a river through which seven bridges are spanned. The question is, can anyone continually bypass them, passing only once across each bridge. And then I was informed that no one has yet been able to do this, but no one has proved that this is impossible.

This question, albeit a banal one, seemed to me, however, worthy of attention by the fact that neither geometry, nor algebra, nor combinatorial art are sufficient to solve it.

From a letter from Leonard Euler to Giovanni Jacobo Marinoni, March 13 [24], 1736 ^{[ 2 ]}



(Judging by the letters of Leonard Euler, the great scientist solved other puzzles with pleasure, too) ..

The problem of the seven bridges

Her decision is set out in detail in letters to Eleur and Marinoni.

Finally, you, glorious husband, express a desire to familiarize yourself with my method of building bridges; I gladly present this method to your judgment. For when you asked me for a solution to this problem, adapted to the special case of Koenigsberg, you probably thought that I proposed this kind of bridge construction, but I did not do it, but only proved that such a construction cannot take place at all. and this should be taken instead of a decision. My method is universal , because with its help, in any case of this kind offered to me, I can immediately decide whether to build a transition using separate bridges or not, and in the first case [I can establish] how this transition should be carried out. Next, I will outline my method, and also describe the way in which I came to him.

Karl Gottlieb Eleler, 03 [14] April 1736

I considered a randomly taken shape of a river branching, as well as bridges a, b, c, d, e, f, as indicated in the figure, and found that a transition is possible, which I imagine as follows. The areas separated from each other by water, I call the letters A, B, C, and when it is supposed to cross the bridge from one area to another, [namely] the transition from A to B through the bridge or a or b is the most convenient to call [ letters] AB, of which the first letter A will denote the area from which they are moving. So, AVSASAV will determine the transition made across all bridges once; the number of these letters must be one more than the number of bridges; this should take place at any possible transition in the manner described, which is easier for everyone to see for himself than to prove. Now I consider how many times the letters ABC should occur in a number of letters A, B, C, A, C, A, B, which should be judged by the number of bridges leading to each of the areas. So, five bridges lead to area A: a, b, c, d, e, and how many times letter A occurs in the middle of that row, so many times there are two of these bridges, because on the one hand you need to go to region A, on the other side - get out of there. If A is found either at the beginning or at the end of that row, then the only bridge transition corresponds to A. It follows that if the number of bridges leading to area A is odd, then all bridges cannot be crossed otherwise than in this way. so that it starts in area A, or ends in area A. And if the number of bridges leading to A is even, then the transition can be made without this condition to start or end in A, but if it starts in A it will have to end there. From this it follows that in the AVSASAV series, any letter, with the exception of the first and last, indicates a transition leading through two bridges to the area designated by this letter.

Therefore, the following rule should be kept: if in any figure the number of bridges leading to a certain area will be odd, then the desired transition across all bridges at the same time cannot be done unless the transition begins or ends in this area. And if the number of bridges is even, no difficulty can arise from this, since neither the beginning nor the end of the transition is recorded. Hence the following general rule: if there are more than two areas to which an odd number of bridges leads, then the desired transition cannot be made at all. For it seems completely impossible for the transition to begin and end in any one of these areas. And if there are only two regions of this kind (since one region of this kind or an odd number of regions cannot be given), then all bridges can be crossed, but with the condition that the beginning of the transition be in one and the end in the other from these areas. When in the proposed figure A and B there are areas to which an odd number of bridges leads, and the number of bridges leading to C is even, then I believe that the transition or the construction of bridges can occur if the transition starts from either A or In, and if someone wants to start the transition from C, then he can never reach the goal. In the location of the Koenigsberg bridges, I have four areas A, B, C, D, mutually separated from each other by water, to each of which leads an odd number of bridges.

Thus, since there are more than two areas to which an odd number of bridges leads, I contend that I have proven the complete impossibility of such a connection of bridges. So, with the help of a very easy rule, it can be almost instantly determined for any shape, is this type of bridges allowed, in which the transition will take place only across all bridges at the same time, or not? For it will be possible to build, if there is no area, or there will be only two, to which an odd number of bridges leads; in such cases, the beginning of the transition is chosen arbitrarily, but there must also be the end of the transition. In the latter case, the beginning of the transition should take place in one of those areas, and the end in the other. Construction is impossible if there are more than two areas to which an odd number of bridges will lead.

Fig. 2. Count Konigsberg bridges.
Fig. 3. Puzzle "Envelope".

Consequently, you can be sure, glorious husband, that this decision in nature, apparently, has little to do with mathematics, and I don’t understand why it is more likely to expect this decision from a mathematician rather than from any other person, because this decision it is supported only by reasoning and there is no need to involve any laws inherent in mathematics to find this solution. So, I do not know how it turns out that questions that have very little to do with mathematics are more likely solved by mathematicians than by other [scientists]. In the meantime, you, glorious husband, determine the place of this question in the geometry of the situation, and as for this new science, I confess, I don’t know what kind of related tasks Leibniz and Wolf wanted. So, I ask you, if you think that I am capable of creating something in this new science, so that you deign to send me several specific tasks relating to it, so that I can better understand myself what it seems desirable. Meanwhile, since I know that You can also make a judgment about the mathematical sciences on the basis of only one task that should be proposed and solved, the beginning of which, at Your request, was proposed by the most glorious Kyun, I would like him to present us with the kind of tasks that he considers it more difficult, [having done this] both for the progress of science and for the exercise of our forces.

Hardly the above reasoning of Leonard Euler aroused in you awe, which, for example, is completely excuse for a person who is somewhat involved in mathematics, admiringly addressing the consequences of Euler’s spectacular formula for complex numbers.


However, you can be impressed by a simple transfer of the merits of this great man to science ...

However, the “problem of the Koenigsberg bridges” ( Fig. 2 ) reminds you of the “envelope”, which you successfully painted in the “first pass” ( Fig. 3 ) in each elementary class this “envelope” multiplying your triumph over your classmates competing with you in this lesson.

How many routes will you find today? I believe that Euler’s letters, which read carefully above, will not make the wrong choice of starting points for building their routes (in the first class you didn’t have such a clue?), And it’s also not difficult to predict where their routes will end. At the same time, reach the eighth bridge in the "city of thinkers" and fill the walking walks of its inhabitants with the desired meaning.

And there could be more bridges ...

In the problem book of Henry E. Dyudeni “520 puzzles” (I have the edition of 1975, Mir Publishing House, Moscow ^{[ 3 ]} ) there are quite a few tasks that can be solved directly by Euler instructions. Let's take a look at one of these tasks, which has been assigned the number 408 in this edition.

Euler armed us with a reliable method, and we will solve the problem of Dudeni 408 easily. However, let's face it, when I started this book, I had no idea about Euler’s recommendations.

• 408. Twenty-two bridges You can see here a diagram of the area with a developed system of irrigation facilities, which shows numerous canals and bridges. A person comes out of one of the areas marked with letters to visit a friend who lives in another area. Wanting to do an exercise at the same time, he passes on each bridge one and only once.

• The puzzle is to find out in which areas the buddies are located. You will find it extremely simple if you think about it for a few minutes. Of course, one should not go beyond the scheme.

Right here is "extremely simple"? ..
...
What if I want to take into account the schedule of city attractions in my itinerary? - For example, part of the bridges along my route are movable, and every time I walk through them I am annoyed that I cannot admire their mechanics in action, or, on the contrary, it is this feature that drives my step in order to pass these bridges before the beginning of the commandant hours

Knowing the path indicated to us by the great mathematician, we are capable, perhaps, of some independent steps. As often happens, if a part of the problem was decided for us, the remaining part is already easier to solve. Knowing where to take the first step, I, perhaps, can write a short instruction for calculating or even dispatching possible routes.


Total, routes, there are 67344 options. It is a bit too much, but true friendship should be able to endure so many visits, it remains to find "real" shoes, because This is a test for her.

Paths and trees

Graphic schemes, of course, are not limited to closed routes, and our path leads us to the trees ...

Since 1978, in a world outside of your computers, here and there, and never here, there are quiet or even almost secret meetings of people unfamiliar to me (I suppose) people called the International Puzzle Party . You can receive an invitation to this event only from a member of this private club. Where and when the next meeting will occur is never known outside the club. If you believe the laconic announcement of the official IPP website, then nothing is more dangerous than the hands of puzzles collectors of puzzles on the party itself. However, after the secret meeting, other mortals happen to see a catalog of outlandish puzzles, carefully inspected by a committee of this elitist forum that is sophisticated in puzzling tasks. One of these puzzles, presented at IPP 37, which took place in August 2017 in Paris (did you also feel attracted to collecting puzzles?), Was proposed by the “non-hinged puzzles forum” (I am not aware of its international movements) as a warm-up for the brain to such leisure to colleagues.

To me, this puzzle seemed somewhat reminiscent of the Dudenie problem, burdened, however, with several nuances.

The developer (creator, creator, demiurge) of this sample of extraordinary thought, a masterpiece of sophisticated human ingenuity marked Donghoon Pee - the creator, apparently modest and undeservedly little known here on Habré, the last injustice we now fix, although, of course, we’ll ruin the intrigue ... I and myself it's a pity to deprive Habr's readers of the opportunity to independently reflect on puzzle 2 & 1 of the author Donghoon Pee - I can only advise those who are eager to solve the puzzle on their own, close the drawings and part of the palm puzzle text below.

Donghoon Pee (Dongun Pi is the most likely read, but in order not to risk, I will use Latin spelling) has his own channel on youtube.com, the Facebook page, he lives in Seoul and is a professional creator (the language doesn’t turn around to say “designer ", Although he himself calls for this kind of activity) puzzles. And his work has repeatedly won the attention of the club IPP. Hopefully, the income of this certainly worthy person will not suffer damage from this publication.

• On a green field of a strictly defined size, you need to place five tiles of different shapes, each of which consists of two colors. The central cell in the field is three-colored - only the corresponding tile color can be in contact with any of the colors of this cell, i.e. if the side strip of the central cell is colored red, with a color other than red, the tile should not touch this side surface of the cell. The goal of the puzzle is to lay all five tiles on the playing field so that each of the three colors of the elements of the tiles form an inseparable color field.

If we continue the analogy with islands and bridges, then, by breaking the field into cells, we can consider these cells as "islands" between which we transfer the "bridges" of the tile. Not to say that our “bridges” will serve anyone as a model of architecture, but, for our narrow task, this convention is quite appropriate. By limiting the conditions of “building bridges” to contacting matching colors in different tiles, and introducing the criterion of “color continuity” (well, of course, it will be logical to start “building” from the central cell), we can start recursively constructing a tree graph that does not turn out to be long, due to the insignificance of the "building material". The root of our tree is the central cell, and multiple branching is permissible in any node of such a tree .



A small modification of the task can turn it into a dense packing problem, etc., but within recognizable limits we can stick to the model allowed by graph theory. Of course, with the increasing seriousness of the task, it may be necessary to take into account the algorithmic complexity and limitations of the recursive mechanism.

Task with four color cubes

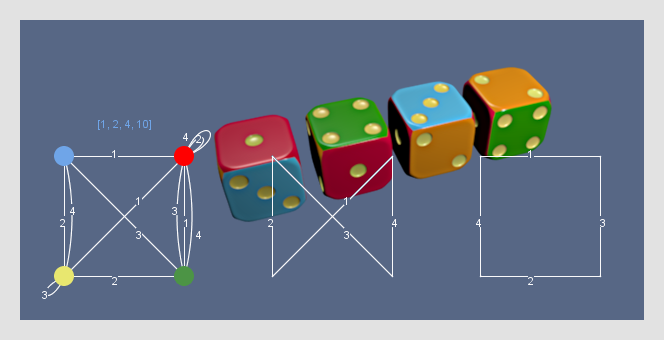
Let's try to give our review the appearance of a little more academic, for which we again turn to the "puzzle with four colored cubes . "

Solving this puzzle with the usual brute force method, we resort to the method that promises us 41472 iterations. The most elegant solution in the graphs will require sorting out combinations of four cubes, described by three pairs of colors. - The difference is palpable. Let me remind the easily algorithmized procedure:

the cube graph in this puzzle is a graphical model , in 4 nodes of which 4 colors are located, and each edge indicates / connects a pair of opposite faces : a clever idea that came to F. De Carteblanche (Cedric AB Smith) was that two sets of four colors each can be described as a graph with nodes of degree 2 , where the nodes themselves mean colors, and the edges of the graph indicate that the pair consists in different, not in one , sets — by matching the pair with the parent cube ( by numbering the edges ), we get unambiguous instructions for placing in the pyramid of this set of faces.

Having instructions for the second set - i.e. for the second pair of faces of the pyramid, we can finally assemble a combination, which is a solution to the puzzle. Thus, selecting from a multigraph (set of graphs of cubes) two subgraphs pointing to different sets of colors, and for this it is enough that the same edge (since exactly the edge indicates a connection) is not used simultaneously in each of the graphs, we get an easy-to-read puzzle solution: we only need, for example, according to the first instruction, to place the cubes in top-to-bottom and bring them in accordance with the second instruction, turning left and right. [Let me remind you that the "loop" is also a node of the 2nd degree]. Of all the subgraphs shown in the figure, only two form a pair with mismatched edges. This is the so-called “only solution” of the “correct” puzzle.


Not superfluous, probably consider in detail an example of a multigraph sweep for a beautiful assembly, which has all 4 colors on each side in 24 positions (the “wrong” puzzle, in the previous publication of the previous publication, is shown in Fig. 6): three subgraphs (in the left figure, these are the three leftmost subgraphs ) can be folded into three pairs with mismatched edges - an assembly with “three solutions” in terminology common in the English-speaking environment.

If I need to “catch symmetrical assemblies” in some, relatively speaking, “stream of cubic entities”, I will try to avoid banal searching. For example, from cubes, sweeps of which are shown in Fig. 2 of the same publication, you can quickly stack 16 sets with "three solutions".

The graph points out to us the inner connection, the unique nature of some thing we are studying. Taking advantage of the observed feature is quite natural, especially if the model promises us some advantage in comparison with other ways of solving the problem.

Reverse modeling

Is it possible to move from the desired graphical model to a concrete implementation of anything? - There is hardly an unambiguous answer, but in most cases I would advise not to try to make such transitions, unless the model you are looking for is limited to features fully described within the graphic prototype. Describing an object from the real world, you neglect a part of its properties in front of one essential feature, for the sake of your chosen model.

For example, in 1073-s unique sets of cubes of four, the number of unique graphs corresponding to these sets is significantly less: if we take into account in the topology of a graph, only a combination of its edges and nodes, omitting the numbering of the edges, then only 204 unique graphs can be identified for four possible puzzles colored cubes.

Decision graphs, those two ways of traversing nodes that need to be distinguished from a multigraph , will be similar, although the original multigraph itself can be divided in different ways, since numbering of faces still makes features in the general topology of the graph. The graphical model we use to find a solution to a puzzle like Instant Insanity characterizes sets of cubes only in terms of optimizing the search for a solution to this puzzle. This model is based on the analysis of the topological structure of a set of cubes for solving only one narrow task - the problem of the relative position of the cubes. A separate multigraph , like the graph of a separate cube, does not indicate the uniqueness of the object, nor should it - we ourselves were looking for something in common in the phenomenon, and not in the object . The portrait image does not appear from the concise characteristic “character - solid, nordic”.


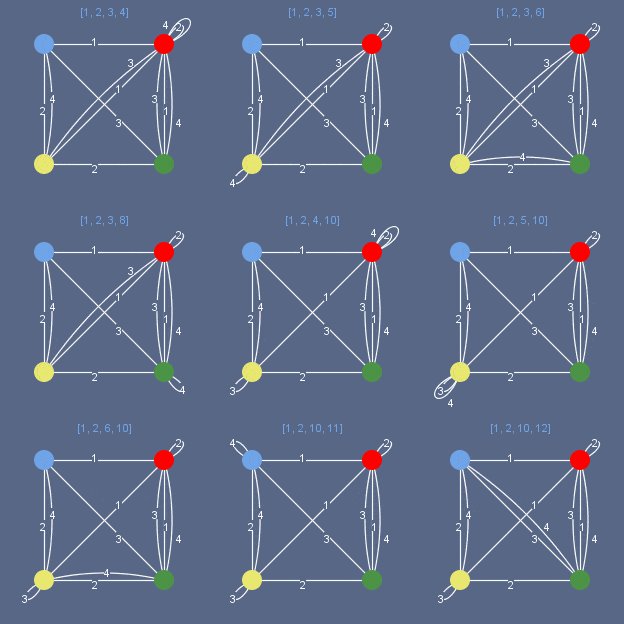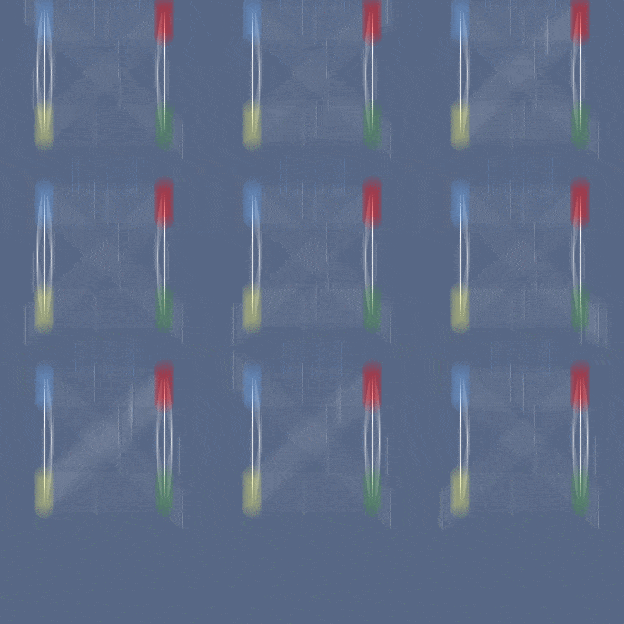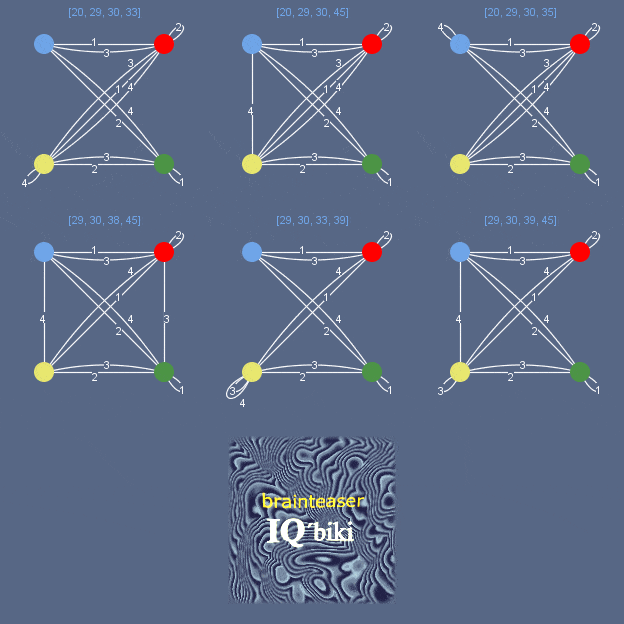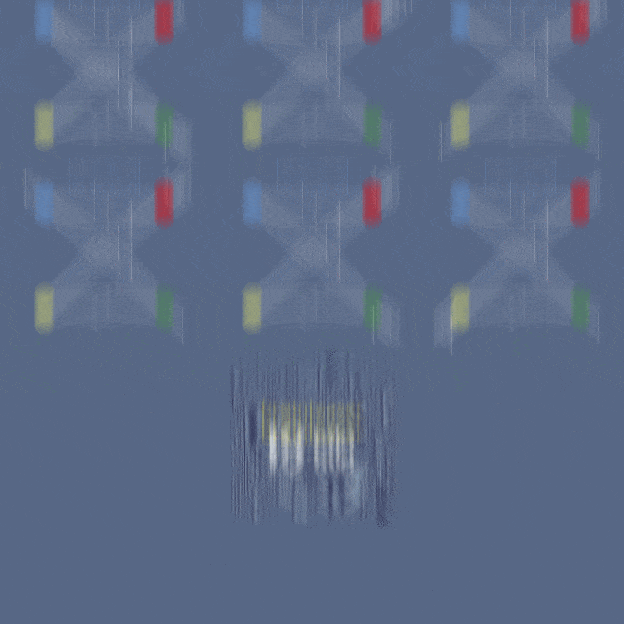
Fig. 4. 204 Count "puzzles with four colored cubes."

Isomorphism

I have only a small hope that someone would peer attentively at the columns I quoted - note - for all! puzzles from four color cubes , and, besides, bothered to make out carefully the graphs of solutions for Instant Insanity and its clones from the site of Robert Stegmann. Meanwhile, this inquisitive hypothetical reader would undoubtedly have a question: “And where, where is this Instant Insanity, replicated by millions of copies? “Is there anything at all similar to any of these graphs?” “But he, nevertheless, is ... However, it is not surprising that this graph cannot be known the first time - here I, however, got excited: from the second or third one, there is no chance of a graph either - this problem is called an isomorphism of graphs .

The graph of Instant Insanity and the countless number of its clones, shyly endowed with their "creators" by different names, can be seen in the left figure. Usually, this picture is accompanied by a sold copy of the puzzle to maintain the spirit in the completely desperate ... (I already hope that the division into subgraphs I have done will hopefully alleviate all their difficulties) It is impossible to recognize this puzzle in the figure below - and this is only one of 1073 possible puzzles from four dice! , just repainted (and probably somewhere existing with a different name).


There are various ways to detect isomorphism of graphs, but the description of any of them, in my opinion, is redundant for an already lengthy article. However, without an illustration of the “miracle of transformation”, some readers may find themselves disappointed, and I prefer her to find other reasons for this.

Let's take a breakdown of the Instant Insanity puzzle on Robert Stegmann's site (R.Stegmann - he is probably “shaken” by the whole IPP club!) - I will follow the following procedure for traversing the faces of the cube: the lower edge → front → upper → back → left → right.

The most common scan of the marked site (the author has collected several clones, but we focus on the "classic" version of the puzzle) will be written in the chosen order of circumvention as follows: RWGGWB, RBBWGG, RGWWRB, GWRBRR.
I hope that no one managed to forget that when recording the graph, we take into account only the pairs of colors of opposite faces, and therefore the lower-case entry of the graphical configuration of the selected cubes looks no different than: RG | WG | WB, RB | BW | GG, RW | GW | RB, GR | WB | RR. As you can see, the multigraph in the first picture fully corresponds to this set (well, except that I have yellow color instead of classic white).

Perhaps it’s not convenient for me alone to work with numbers, so we’ll mark colors with numbers (and exclude some disagreement in colors noted above), and at the same time we write this combination of cubes at once in the solution position (the good thing is that we have two subgraphs indicating our way before your eyes):

• R = 0, W = 1, B = 2, G = 3
• After that, replace the colors ( “repaint the cubes” ) as follows:
  0 → 1, 1 → 2, 2 → 3, 3 → 0
• and at the end each of them will be rotated twice by 90 degrees around the "long" axis of the pyramid (in terms adopted in the previous publication, this is equivalent to rearranging the faces in the order of 230145 , these are, of course, not colors, but indices )

[0, 1, 3, 3, 1, 2] → [1, 2, 0, 0, 2, 3] → [0, 0, 1, 2, 2, 3] : RW|RB|BG
[2, 2, 0, 1, 3, 3] → [3, 3, 1, 2, 0, 0] → [1, 2, 3, 3, 0, 0] : WG|BG|RR
[3, 0, 1, 2, 0, 1] → [0, 1, 2, 3, 1, 2] → [2, 3, 0, 1, 1, 2] : BR|GW|WB
[1, 3, 2, 0, 0, 0] → [2, 0, 3, 1, 1, 1] → [3, 1, 2, 0, 1, 1] : GB|WR|WW

You can compare the resulting graph with what is placed below the Instant Insanity graph, and make sure that it is the same graph.

Instead of conclusion

I really hope that the reading was not boring. Perhaps someone has been somewhat helpful. And I am almost certain that the number of drawn envelopes will slightly increase by tomorrow, and someone will finally find the strength and motivation to distract the heir from his gadget by some entertaining and intelligent task. Euler did not neglect ...

---

1. ↑ Leonard Euler. Letters to Scientists, Publishing House of the Academy of Sciences of the USSR, 1963, p.339
2. ↑ Leonard Euler. Letters to Scientists, Publishing House of the Academy of Sciences of the USSR, 1963, p. 153
3. ↑ Henry E. Dewdeni. 520 puzzles. Compiled and edited by the American edition M. Gardner, MIR Publishing House, Moscow, 1975

---