Lindenmeyer systems

Natural patterns

Lindenmayer system invented the Hungarian biologist Aristide Lindenmayer, studying the growth of algae. He developed the L-system as a way of describing the growth of algae and simple plants. The result was a kind of language in which it was possible to express the properties of recursiveness and self-similarity of growth of the organism. In fact, L-systems can be used to generate natural patterns; In addition, well-known mathematical patterns can also be written in the form of an L-system. In this article, I will talk about the different types of L-systems and demonstrate them by drawing the "turtle graphics" of two-dimensional and three-dimensional Lindenmeyer systems .

The language is very simple, it consists of symbols (alphabet) and production rules. The first state of a sentence is called an axiom . Production rules for the evolution or growth of a system can be repeatedly applied to this axiom. As a simple example, you can take the system with the axiom $$$A$and by the rule $$$A \ to ABA$. After the first iteration (the first time the rule is applied), the sentence changes to $$$ABA$. After the second iteration, the sentence will look like $$$ABABABA$, and so on. You can see how the self-expanding proposal becomes an analogue of cell division in plants and other biological processes.

[A ... Z]	Any (non-constant) letter of the alphabet moves the bug forward a fixed distance.
+	Rotate the turtle to the right by a fixed number of degrees
-	Turn the turtle to the left by a fixed number of degrees
[	Write the current state of the turtle to the stack
]	Retrieving the last state of the turtle from the stack and assigning this state

Figure 1: Alphabet for drawing a two-dimensional Lindenmayer system

Drawing sentences

After the system is set and all the iterations are completed, we get a big offer with interesting properties. To visualize these properties, we need to create a way to render them. In this article, I will render the system with the help of “snail graphics” .

The turtle graphic is rendered by placing the turtle on the Cartesian plane and passing instructions to it. The turtle moves in accordance with its instructions. The turtle does the drawing, leaving a trail behind it. In our case, each character from the L-system clause is sent to the turtle. In the short example presented above, the sentence is quite simple, it contains only letters. It is difficult to convert a string of letters into interesting instructions for the bug. Therefore, special characters are set for encoding commands to the turtle. Figure 1 shows the key to my turtle tongue.
')
Below, I have implemented an interactive (in the original article) renderer of Lindenmayer 2D systems. There are several examples in it, and you can also set your own systems of six production rules. I added a field constants , which contains a string of characters. When rendering a string with a bug, it will ignore all characters that are constants. However, constant symbols are still subject to the rules. The angle field indicates the number of degrees the turtle is rotated with the + and - commands. In the fields of the rules you can use the constant AXIOM . It will be replaced with the original axiom. This is used in several examples.


The source code of this javascript example is in the repository . Examples of systems shown demonstrate some of the capabilities of the Lindenmayer systems, from noisy, similar to random patterns to rigorous geometric patterns. All systems exhibit self-similarity property; when the number of iterations becomes high, the small parts created are no longer visible. However, in theory, we can reduce the scale indefinitely, while increasing accuracy. This is a well-known property of fractals . When reducing the scale of fractals, the same patterns are often seen as on a larger scale.

Add dimensions

The example shown above can fully demonstrate the properties of the Lindenmayer systems, but I want to add a few more characteristics to make the algorithm even more powerful. Personally, I am very interested in using Lindenmayer’s 3D systems to generate plants and natural systems. A very interesting source of information on this topic is the website of the Calgary University Biological Modeling and Visualization Group . On this subject there are many articles that are presented on this website.

I want to keep my system as simple as possible, but I lack some features that are necessary to create more complex systems. I would like to at least model the following:

• There must be the possibility of some randomization, because we believe that in nature there is an accident of forms
• I want characters to keep track of their age, because in nature, the behavior of cells can depend on their age
• Production rules must take into account the context of the characters.
• I want to track the distance to the root cell
• The turtle should be able to move in three dimensions, which will allow you to create more complex forms

Implement movement in three dimensions is not so difficult. Instead of moving on a Cartesian plane, the turtle will be a position in the quaternion. At each step, I will add a unit vector (upward), rotated by this quaternion to the turtle position, and the quaternion itself will be rotated when the turn symbols meet. Modeling other features as simple as possible will be a bit more tricky task.

[A ... Z]	Any (non-constant) letter of the alphabet moves the bug forward a fixed distance.
+	Yaw turtle to the right at a fixed angle
-	Yaw turtle left at a fixed angle
/	Turtle roll to the right at a fixed angle
\	Turtle roll to the left at a fixed angle
^	Turtle pitch up at a fixed angle
_	Turtle pitch down to a fixed angle
[	Write the current state of the turtle to the stack
]	Retrieving the latest status of the turtle from the stack and assigning it

Figure 2: Alphabet for drawing a three-dimensional Lindenmayer system

Parametric grammar

To simplify the new features, I need to expand the alphabet and syntax. Figure 2 shows the key of this new system. New table symbols are rotation symbols required to move a bug in 3D space.

Randomness is easy to model by adding one set of fuzzy production rules. If a symbol has several rules, then one of them is randomly selected.

To simulate cell age and root distance, I could add two variables to each symbol. If I then needed to add other properties, I would have to add new variables. Such an approach would not be very flexible and very specific. Fortunately, there is a more general solution: Lindenmeier parametric systems . In parametric L-systems, each symbol is followed by a list of parameters (if any). Production rules can be applied to symbols with a specific set of parameters or for certain conditions of these parameters; In addition, the symbols obtained using the rule can also have their own parameters.

I will demonstrate this new system on the example of a symbol with one parameter (the age of a symbol, measured in the number of iterations). Let axiom be $$$A (0)$, and the only production rule - $$$A (x) \ to A (x + 1)$. At each iteration, the parameter of each character $$$A$will increase by one. Now I want to change each character $$$A$on $$$B$when he reaches the age of eight iterations. The production rule will be $$$A (x): x == 8 \ to B$. If I set a production rule for this system $$$A (x, y) \ to C$, it will never apply: there will be no symbol in the system $$$A$with two parameters. It is worth considering that $$$x$and $$$y$in these examples are chosen arbitrarily; they are used to work with parameter values. There are no specific names for these parameters. $$$x$and $$$y$- these are just variables and can be any character.

I added two syntactic rules to the language: the number of parameters separated by commas is indicated in parentheses, and the first operand of the production rule can be followed by a symbol $$$:$if it should be satisfied only under the condition after this symbol. Parametric grammar allows you to implement much more extensive features than I originally needed.

Context-sensitive grammar

The system is almost complete. The last thing I want to encode is the context. The context of the symbol should influence the rules applied to it. Theoretically, I could encode the context in the parameters of the characters, but in this case a very complex system of rules and parameter lists would result. So instead, I add one final syntax rule to the production methods.


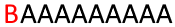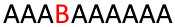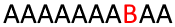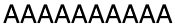
Figure 3: Lindenmayer context-sensitive system in action

Suppose I have an axiom consisting of several $$$A$and one $$$B$at the beginning and I want to $$$B$moved one step to the right on each iteration, without changing the length of the sentence. This can be implemented using context-sensitive rules. First, I will add a rule $$$B <a \ to b$. It should be read as follows: $$$A \ to b$if the character $$$A$preceded $$$B$. At each iteration in which this rule applies, each character $$$A$to the left of which is $$$B$will change to $$$B$. Now I just need to $$$B$moved, so after each iteration $$$B$must become again $$$A$to all $$$A$over time did not turn into $$$B$. This is implemented by a simple rule. $$$B \ to a$. Figure 3 shows this system evolving over eleven iterations, and the initial axiom is $$$BAAAAAAAAA$.

This context-sensitive grammar is compatible with the parametric grammar described above. Suppose I have a sentence of several occurrences $$$A (x)$where value $$$x$for different characters different. I want to write a context-sensitive production rule that replaces $$on $$$B$only when $$$A$surrounded by other occurrences $$$A$whose parameters are equal; in other words, left and right should be $$$A$with the same parameter values. The production rule is as follows:

$$

$$A (x) <A (y)> A (z): x == z \ to B$$

That is, the latest additions to the grammar are the characters $$$<$and $$$>$. If the left operand of the production rule is preceded by $$$<$, then as a context it needs a character before $$$<$. If it follows $$$>$, it needs a character after context $$$>$. The production rules may also have no context, or only a right / left context.

Lindenmayer's three-dimensional context-sensitive parametric system

Now everything is ready for creating a renderer of a three-dimensional Lindenmayer context-sensitive parametric system, which I have implemented below (in the original article). It contains all the features described in this article. Most of the fields of the previous 2D renderer are copied, but in this system a button for step-by-step evolutionary change and the print function of the final sentence are added. The parser of context-sensitive parametric systems Lindenmayer is located in this repository .

Implemented several rendering modes. The generated 3D image can be rotated by dragging the mouse (or finger on the touch screen) and scale the mouse wheel. The source code for this renderer is on GitHub . Click the Go button to generate the current system.

Conclusion

Lindenmayer systems allow you to create very interesting and natural patterns that can be useful in many areas. In addition to modeling fractals, they can be used to generate natural content, such as trees and plants. Another application is the generation of a procedural environment in which context-sensitive rules play an important role. I suspect that the Lindenmayer system can be changed using genetic algorithms, slightly changing the production rules. This can be a very interesting way for the evolutionary change of plants, and I want to experiment with it if there is free time.

It seems that L-systems are able to simulate nature with a certain degree of accuracy. It is curious to what extent they can actually model the processes of natural growth using the rules I discovered?