The book "Deep learning. Immersion in the world of neural networks "

Hi, Habrozhiteli! Recently, we published the first Russian book about deep learning from Sergey Nikolenko, Arthur Kadurin and Ekaterina Arkhangelskaya. Maximum explanations, minimum code, serious material about machine learning and fascinating presentation. Now we will consider the section “Computation Graph and Differentiation on It” in which the fundamental concept for the implementation of learning algorithms for neural networks is introduced.

If we manage to present a complex function as a composition of simpler ones, then we can effectively calculate its derivative with respect to any variable, which is what is required for the gradient descent. The most convenient representation in the form of a composition is the representation in the form of a calculation graph. A computation graph is a graph whose nodes are functions (usually fairly simple, taken from a predetermined set), and the edges associate functions with their arguments.

It is easier to see with your own eyes than to formally define; look at pic 2.7, where three calculation graphs are shown for the same function:


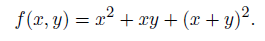
In fig. 2.7, and the graph turned out to be quite straightforward, because we allowed the use of the unary function “squaring” as vertices.
')

And in fig. 2.7, b, the graph is a bit more cunning: we have replaced the obvious squaring with ordinary multiplication. However, it didn’t greatly increase in size because of the calculation graph in fig. 2.7, b it is allowed to reuse the results of previous calculations several times and it is enough to simply submit the same x two times to the input of the multiplication function to calculate its square. For comparison, we drew in Fig. 2.7, in the graph of the same function, but without reuse; now it becomes a tree, but in it one has to repeat entire large subtrees, from which several paths to the root of the tree could go out at once.

In neural networks, the functions from which neurons are derived are usually used as basic, elementary functions of a computation graph. For example, the scalar product of vectors enough to build any, even the most complex neural network composed of neurons with the function 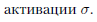One could, by the way, express the scalar product through addition and multiplication, but it is also not necessary to “crush” too: elementary can be any function for which we can easily calculate its own and its derivative with any argument. In particular, any functions of neuron activation, which we will discuss in detail in section 3.3, are perfect.

So, we realized that many mathematical functions, even with very complex behavior, can be represented as a calculation graph, where the nodes have elementary functions, from which, like bricks, we get a complex composition, which we want to calculate. Actually, using such a graph, even with a not too rich set of elementary functions, it is possible to approximate any function arbitrarily accurately; we'll talk about this a little later.

Now back to our main subject - machine learning. As we already know, the goal of machine learning is to choose a model (most often we mean the weight of a model specified in a parametric form) so that it best describes the data. The “best of all” here, as a rule, refers to the optimization of a certain error function. Usually it consists of the actual error on the training sample (likelihood function) and regularizers (a priori distribution), but now we just need to assume that there is some rather complicated function that is given to us from above, and we want to minimize it. As we already know, one of the most simple and universal methods for optimizing complex functions is the gradient descent. We also recently found out that one of the most simple and universal methods to define a complex function is the calculation graph.

It turns out that the gradient descent and the calculation graph are literally made for each other! As you were probably taught at school (the school program generally contains a lot of unexpectedly deep and interesting things), to calculate the derivative of the composition of functions (at school it was probably called a derivative of a complex function, as if the word “complex” does not have enough values), it is enough to be able to calculate the derivatives of its components:



The rule is applied to each component separately, and the result is
again quite expected:


Such a matrix of partial derivatives is called the Jacobi matrix, and its determinant is
Jacobian; they will meet again and again. Now we can calculate the derivatives and gradients of any composition of functions, including vector functions, and for this we need only to be able to calculate the derivatives of each component. For a graph, all this de facto boils down to a simple, but very powerful idea: if we know the graph of computations and know how to take the derivative at each node, this is enough to take the derivative of the entire complex function that the graph sets!


Let's first analyze this with an example: consider the same calculation graph that was shown in Fig. 2.7. In fig. 2.8, and the elementary functions making the graph are shown; we marked each node of the graph with a new letter, from a to f, and wrote out the partial derivatives of each node at each input.

Now you can calculate the partial derivative 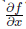as shown in fig. 2.8, b: we begin to calculate the derivatives from the sources of the graph and use the formula for differentiating the composition to calculate the next derivative. For example: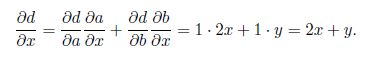


But you can go in the opposite direction, as shown in Fig. 2.8 in. In this case, we start from the source, where the private derivative is always and then we expand the nodes in the reverse order according to the formula for differentiating a complex function. The formula will apply here in the same way; for example, at the lowest node we get: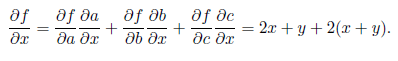


Thus, it is possible to apply the formula of differentiation of a composition on a graph or from sources to drains, obtaining partial derivatives of each node with the same variable 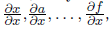either from effluent to source, receiving partial derivatives of effluent at all intermediate nodes 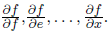Of course, in practice for machine learning we need the second option rather than the first: the error function is usually the same, and we need its partial derivatives for many variables at once, especially for all weights that we want to use for gradient descent.

In general, the algorithm is as follows: Suppose we are given a certain directed acyclic calculation graph G = (V, E), whose vertices are functions 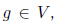, moreover, part of the vertices corresponds to the input variables x1, ..., xn and has no incoming edges, one vertex has no outgoing edges and corresponds to the function f (the whole graph calculates this function), and the edges show the dependencies between the functions in the nodes. Then we already know how to get the function f standing in the “last” vertex of the graph: to do this, it is enough to move along the edges and calculate each function in topological order.

And to learn the partial derivatives of this function, it is enough to move in the opposite direction. If we are interested in partial derivatives of functions 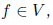then in full accordance with the formulas above, we can calculate for each node 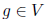in this way:


This approach is called the backpropagation algorithm (backpropagation, backprop, bprop), because the partial derivatives are calculated in the opposite direction to the edges of the calculation graph. And the algorithm for calculating the function itself or the derivative with respect to one variable, as in Fig. 2.8, b, is called forward propagation algorithm (fprop).

And the last important note: note that for all the time while we were discussing graphs of calculations, differentials, gradients, and the like, we, actually, never seriously mentioned neural networks! Indeed, the method of calculating derivatives / gradients according to the computation graph is in no way connected with neural networks. This is useful to keep in mind, especially in practical matters, to which we will proceed in the next section. The fact is that the Theano and TensorFlow libraries, which we will discuss below and where most of the deep learning is done, are, generally speaking, libraries for automatic differentiation, and not for neural network training. All that they do is allow you to set the graph of calculations and damn efficiently, with parallelization and transfer to video cards, they calculate the gradient according to this graph.

Of course, “on top” of these libraries you can implement the library itself with the standard designs of neural networks, and this is also what people constantly do (we will consider Keras below), but it is important not to forget the basic idea of ​​automatic differentiation. It can be much more flexible and rich than just a set of standard neural structures, and it may happen that you will be extremely successful in using TensorFlow not at all to train neural networks.

»More information about the book can be found on the publisher's website.
» Table of Contents
» Excerpt

For Habrozhiteley a discount of 20% for the coupon - Deep learning