Using the inverse Laplace transform to analyze the dynamic links of control systems
Hello!
Until now, in the arsenal of high-level Python programming language tools, there were no modules for the numerical conversion of the transfer functions of ACS elements from the frequency domain to the time domain.
')
Since the functions of the inverse Laplace transform are widely used in the analysis of dynamic measurement and control control systems, the use of Python for these purposes was very difficult, since it was necessary to use a less accurate inverse Fourier transform [1].
This problem is solved by the free distribution mpmath module of the Python library (under the BSD license), designed to solve real and complex floating-point arithmetic problems with a given accuracy.
Fredrik Johansson [2] began working on the module in 2007, and, thanks to the help of many project participants, mpmath has now acquired the capabilities of a serious mathematical package.
However, we will be interested only in the topic stated in the article, which is implemented using the invertlaplace one-step algorithm. As an example, consider a comparison of the results of the inverse Laplace transform of the transfer function w (p) = 1 / (1 + p) ** 2 using an invertlaplace with the known transition function h (t) = e ** - t from the specified transfer function:
Invertlaplace testing
from mpmath import * import time mp.dps = 15# , mp.pretty = True start = time.time() def run_invertlaplace(tt,fp,ft): for i in range(0,len(tt)): print(' : %s'%ft(tt[i])) print(' : %s'%invertlaplace(fp,tt[i],method='talbot')) print(' h(t) : %s. :%s.'%(ft(tt[i]), ft(tt[i])-invertlaplace(fp,tt[i],method='talbot'))) stop = time.time() print (", : %s"%(stop-start)) tt = [0.001, 0.01, 0.1, 1, 10]# fp = lambda p: 1/(p+1)**2# ft = lambda t: t*exp(-t)# run_invertlaplace(tt,fp,ft) Test results:
The value of the test function: 0.000999000499833375
The resulting value of the function: 0.000999000499833375
H (t) value: 0.000999000499833375. Absolute error: 8.57923043561212e-20.
Test function value: 0.00990049833749168
The resulting value of the function: 0.00990049833749168
H (t) value: 0.00990049833749168. Absolute error: 3.27007646698047e-19.
The value of the test function: 0.090483741803596
The resulting value of the function: 0.090483741803596
H (t) value: 0.090483741803596. Absolute error: -1.75215800052168e-18.
The value of the test function: 0.367879441171442
The resulting value of the function: 0.367879441171442
H (t) value: 0.367879441171442. Absolute error: 1.2428864009344e-17.
The value of the test function: 0.000453999297624849
The resulting value of the function: 0.000453999297624849
The value of h (t): 0.000453999297624849. Absolute error: 4.04513489306658e-20.
The time spent on the inverse Laplace transform: 0.18808794021606445
The test example is limited in scope, but it also shows that the one-step invertlaplace algorithm has high accuracy and non-critical execution time for a limited number of time values.
In the considered example, the talbot method was used, the features of other methods can be found in the documentation [3].
However, it should be borne in mind that all numerical methods of the inverse Laplace transform require that their abscissa be shifted closer to the origin of coordinates for longer times. If the abscissa moves to the left of the rightmost coordinate in the Laplace region, the answer will be completely wrong.
Therefore, it is necessary to conduct a study of the applicability of the numerical inverse Laplace transform for certain transfer functions and evaluate the error in comparison with another method, in this publication it is the method of the inverse Fourier transform.
1. Construction of the transient characteristics of the control object by its transfer function using invertlaplace
Suppose we have a water-to-water heat exchanger with a transfer function along the channel, the temperature of the heated water is the heating water flow. The Laplace transform of the output signal is the transfer function of the control object multiplied by 1 / p (unit perturbation of the heating water flow) taking into account the delay τ has following view:
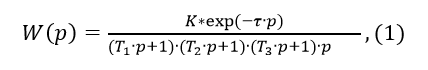
where: Ti - time constants of links; K - static transfer coefficient; p ¬ Laplace operator.
The inverse Laplace transform of the transfer function (1)
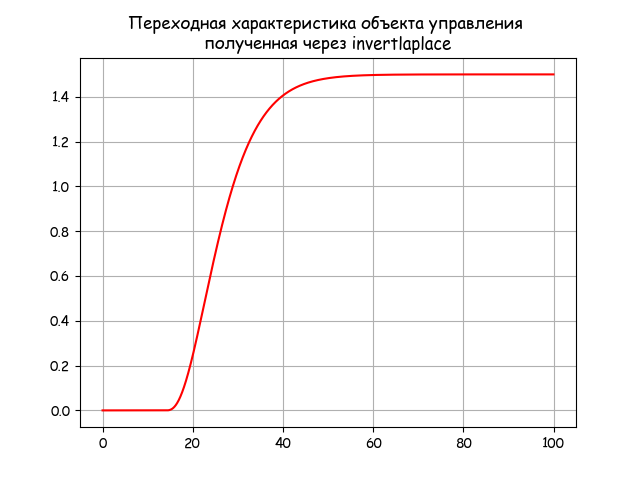
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' mp.dps = 5; mp.pretty = True def run_invertlaplace(tt,fp,tau): y=[] for i in np.arange(0,len(tt)): if tt[i]<=tau: y.append(0) else: y.append(invertlaplace(fp,tt[i],method='talbot')) return y tau=5 tt = np.arange(0,100,0.05) T1=5;T2=4;T3=4;K=1.5;tau=14 fp = lambda p: K*exp(-tau*p)/((T1*p+1)*(T2*p+1)*(T3*p+1)*p) y=run_invertlaplace(tt,fp,tau) plt.title(' \n, invertlaplace ') plt.plot(tt,y,'r') plt.grid(True) plt.show() We obtain the transient characteristic of the object with delay and self-leveling:
2. Construction of the transient response of the PID controller based on its transfer function using invertlaplace
The Laplace image of the transfer function of the PID controller is:
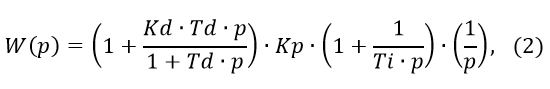
where: Td, Ti are the time constants of the differentiating and integrating units; Kp, Kd - static transfer coefficients of proportional and differentiating units;
p is the Laplace operator.
The inverse Laplace transform of the transfer function (2)
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' mp.dps = 5; mp.pretty = True tt = np.arange(0.01,20,0.05) Kp=2;Ti=2;Kd=4;Td=0.5 fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p) y=[invertlaplace(fp,tt[i],method='talbot') for i in np.arange(0,len(tt))] Kd=0 fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p) y1=[invertlaplace(fp,tt[i],method='talbot') for i in np.arange(0,len(tt))] plt.title(' \n, invertlaplace ') plt.plot(tt,y,'r', color='r',linewidth=2, label='-') plt.plot(tt,y1, color='b', linewidth=2, label='-') plt.grid(True) plt.legend(loc='best') plt.show() By the listed listing, you can get not only the transient response of the PID controller, but also the PI controller, by adopting Kd = 0:
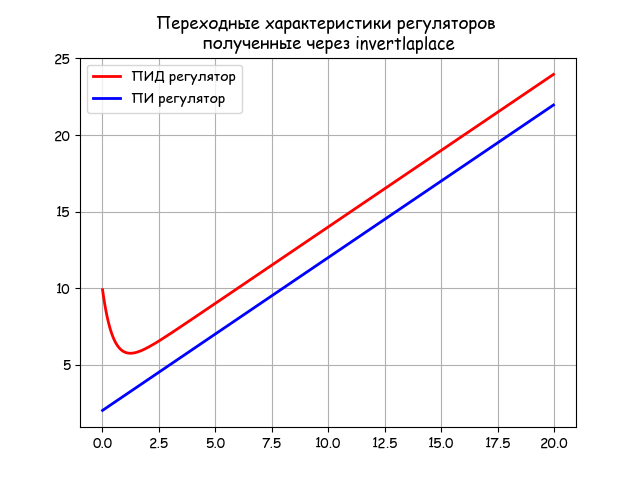
3. Evaluation of the accuracy of the numerical method of the inverse Laplace transform invertlaplace as applied to typical SAU objects
Taking into account the precautions regarding the applicability of invertlaplace given at the beginning of the article, the following presentation proved the applicability of the method to objects with delay and self-alignment, as well as to the regulators.
It remains to the end not clarified the question of the accuracy of a numerical solution. For clarification, we use the transfer function (2) and the following exact conversion to the transition function given in [1]:
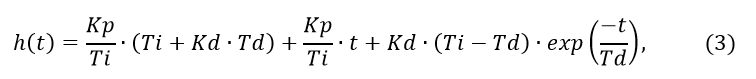
Accuracy of the inverse transform (2) using the test function (3)
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' mp.dps = 15; mp.pretty = True tt = np.arange(0.01,20,0.01) Kp=2;Ti=2;Kd=4;Td=0.5 fp = lambda p: (1+(Kd*Td*p)/(1+Td*p))*Kp*(1+1/(Ti*p))*(1/p) ft = lambda t:(Kp/Ti)*(Ti+Kd*Td)+(Kp/Ti)*t+Kd*(Ti-Td)*exp(-t/Td) y=np.array([invertlaplace(fp,tt[i],method='talbot') for i in np.arange(0,len(tt))]) y1=np.array([ft(tt[i]) for i in np.arange(0,len(tt))]) z=y-y1 plt.title(' invertlaplace ') plt.plot(tt,z,'r', color='r',linewidth=1, label=' ') plt.grid(True) plt.legend(loc='best') plt.show() We get the following schedule:
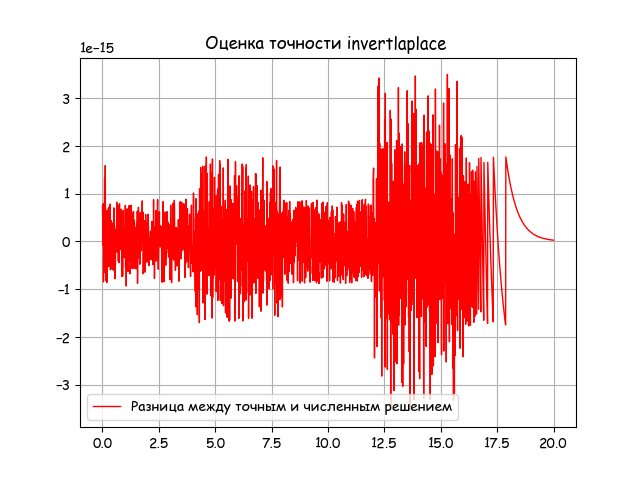
From the graph it is seen that the error of the numerical method for the reduced class of transfer functions is negligible (3 * 10 ^ -15). In addition, the accuracy of the numerical method can be controlled by setting the values mp.dps and the step tt [i + 1] -tt [i] (see listing).
4. Comparative evaluation of the accuracy of the numerical inverse Laplace transform method and the inverse Fourier transform numerical method applied to typical ACS objects
The construction of the transient response can be made on the basis of the formula for the inverse Fourier transform [1]:
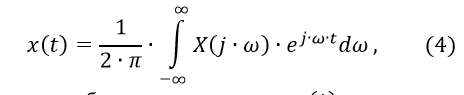
where X (j ∙ ω) is the Fourier image of the original x (t)
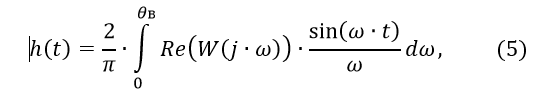
where Re (W (j ∙ ω)) is the real frequency response of the control object.
As the upper limit of integration θb, the frequency ωc is taken in the calculation, at which the module Re (W (j ∙ ω)) decreases to a certain small value (for example, 0.05 * K) and does not exceed this value with a further increase in ω.
First, we define the upper limit of integration in relation (5). To do this, we use the transfer function (1), after getting rid of a single impact, multiplying the right-hand side by the operator p.
Plotting the function Re (W (j ∙ ω))
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' ww= np.arange(0,0.6,0.005) T1=25;T2=21;T3=12;K=0.37;tau=14 def invertfure(w): j=(-1)**0.5 return ((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real) z=[invertfure(w) for w in ww] plt.title(' \n Re(W(j*w)) ') plt.plot(ww,z,'r') plt.grid(True) plt.show() Schedule:
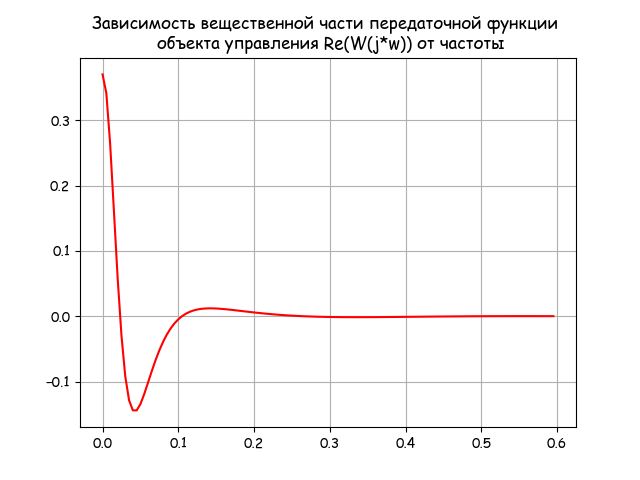
It is clear from the graph that the upper limit of integration in relation (5) can be taken equal to 0.6, since with a further increase in the frequency, the real part of the transfer function of the control object retains a zero value.
Using (5), we obtain the transient response of the control object using the inverse Fourier transform method:
Fourier transient response
# -*- coding: utf8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl from mpmath import * mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' from scipy.integrate import quad tt=np.arange(0,200,1) T1=25;T2=21;T3=12;K=0.37;tau=14 def invertfure(w,t): j=(-1)**0.5 return (2/np.pi)*((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real*(np.sin(w*t)/w)) z=[quad(lambda w: invertfure(w,t),0, 0.6)[0] for t in tt] plt.title(' , \n ') plt.plot(tt,z,'r') plt.grid(True) plt.show() 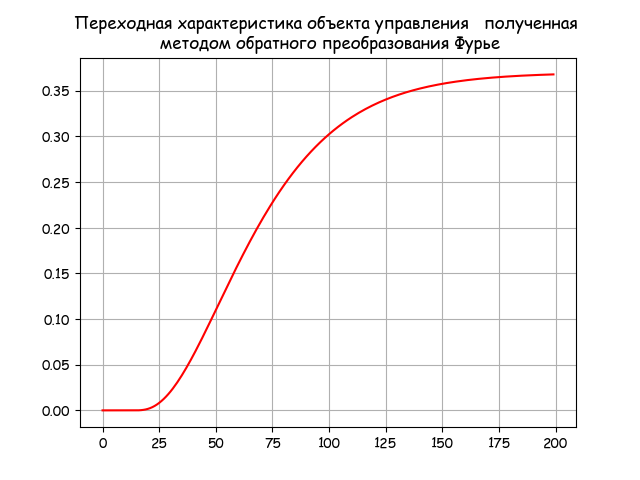
For a comparative assessment of the accuracy of the inverse Laplace transform and Fourier transform, we use the exact transform of the transfer function (1) of the control object given in [1]:
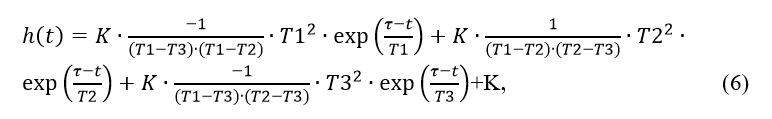
From the exact transform (6) we subtract in turn the inverse Laplace transform (1) and the inverse Fourier transform. To build a graph characterizing the comparison of the accuracy of both methods, we make the following program listing:
Comparative analysis of the methods of inverse Laplace and Fourier transforms
# -*- coding: utf8 -*- import numpy as np from scipy.integrate import quad import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' tt = np.arange(0,100,0.01) T1=25;T2=21;T3=12;K=0.37;tau=14 def invertfure(w,t): j=(-1)**0.5 return (2/np.pi)*((K*np.exp(-tau*j*w)/((T1*j*w+1)*(T2*j*w+1)*(T3*j*w+1))).real*(np.sin(w*t)/w)) z=np.array([quad(lambda w: invertfure(w,t),0, 0.6)[0] for t in tt]) def h(t): if t<=tau: g=0 else: g=(-K*(T1**2)*np.exp((tau-t)/T1)/((T1-T3)*(T1-T2)))+(K*(T2**2)*np.exp((tau-t)/T2)/((T1-T2)*(T2-T3)))+(-K*(T3**2)*np.exp((tau-t)/T3)/((T1-T3)*(T2-T3)))+K return g q=np.array([h(t) for t in tt]) from mpmath import * mp.dps = 5; mp.pretty = True def run_invertlaplace(tt,fp,tau): y=[] for i in np.arange(0,len(tt)): if tt[i]<=tau: y.append(0) else: y.append(invertlaplace(fp,tt[i],method='talbot')) return y fp = lambda p: K*exp(-tau*p)/((T1*p+1)*(T2*p+1)*(T3*p+1)*p) y=np.array(run_invertlaplace(tt,fp,tau)) plt.title(' \n ') plt.plot(tt,qy,'b',linewidth=2, label= ' ') plt.plot(tt,qz,'r',linewidth=2, label=' ') plt.legend(loc='best') plt.grid(True) plt.show() 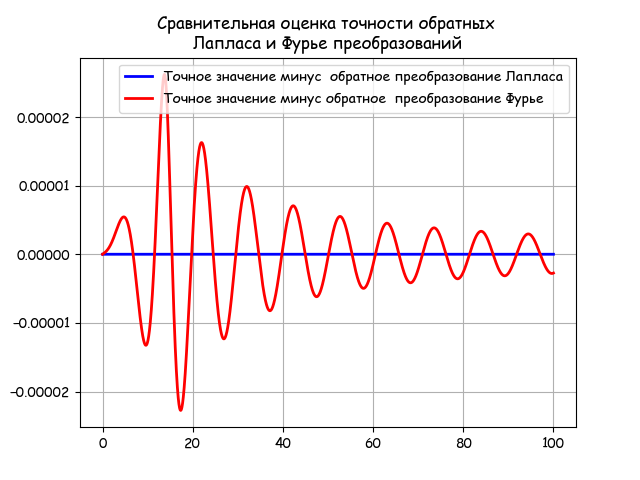
From the graph it follows that the numerical inverse Laplace transform is more stable than Fourier and, in addition, it coincides with the exact solution.
findings
1. A comparative analysis of the numerical methods of the inverse Laplace and Fourier transforms is carried out, the greater accuracy and stability of the inverse Laplace transform is shown.
2. The possibilities of using the mpmath Python library for the inverse Laplace transform of the main transfer functions of objects and ACS elements are shown.
Links
Source: https://habr.com/ru/post/346338/
All Articles