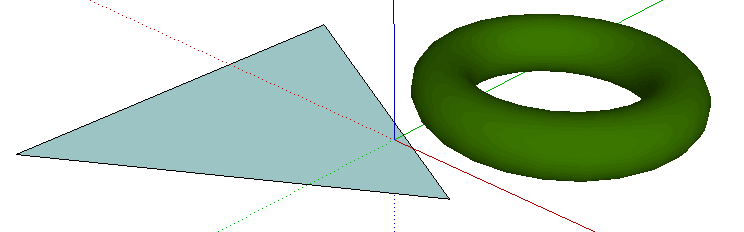
Visualization of discrete space: a torus versus a simplex
Imagine that the concept of distance itself is artificial and not intrinsic to reality. Can we think of ourselves, and even better visualize the world without distances? The article proposes one of the ways to do this with the help of several mathematical concepts, namely, discrete space, simplex and torus. From the discussion of these concepts, several conclusions are drawn regarding the visualization of multidimensional data.
Space with the same distance between points
Distance is a measure of how much one object is closer or farther from another. We encounter the idea of distance in our very early childhood when we try to reach for a toy. Then we begin to walk and ride, developing the ability to reach objects that are farther and farther from where we are now. Entire industries (transport, mail, telecommunications) are based on the fact that there are certain distances through which people and goods need to be transported or information should be transmitted. Various devices, such as binoculars, can reduce the distance, at least visually.
Also, the distance can be used indirectly. When visualizing data, the distance between points and other objects is used to show the relationship between other quantities. In devices, the “closer-further” idea appears as an analogue of “colder-warmer” (thermometer scale), “lighter-heavier” (scale of weights), “slower-faster” (speedometer scale). We can measure the distance for its own sake, both on the way and to understand the values of any variables.
We have no difficulty to conceive the distance. Moreover, it turns out naturally.
In mathematics, distance is related to the concept of metric space . The distance (metric) is defined between any two points (elements, objects) of a metric space. The metric is a quantitative expression of the "closer-farther" relationship, that is, it answers the question of how much closer and how much farther. Geometrically and geographically, the metric has an obvious meaning and is expressed in kilometers, miles, and similar units. In a general sense, a metric can have any meaning, for example, a rating of participants in a competition. In this case, the metric is the number of points scored, and the starting point is first place.
All these examples were needed to show how important the concept of distance is to our lives. Can we think life without distance? With the advent of the Internet, it has become easier in terms of communication, but many other aspects of our life are still strongly associated with the concept of distance. Nevertheless, we can create a mathematical abstraction in which the metric d is constant and equal, for example, to unity. Such an abstraction already exists and is called a discrete space X :
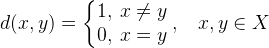
In this definition, x and y are any two points (elements, objects) of a space. The definition implies that all points are equally far away or equally close to each other. Taking any point we will see that the distance to any other is the same. Moving from point A to point B, all other things equal, takes the same amount of time. Moreover, at point B, the situation is the same - again, the distance to any other point will be the same as to point A.
Discrete space is easy to present in the form of a table of distances , as is done in a car atlas. At the intersection of the row and column in such a table indicates the distance for points corresponding to a given row and column of the table. According to the definition, for a discrete space on the diagonal of such a table will go zeros, all the other values of the unit. An example for a space consisting of six points from A to F:

Or with cities (in kilometers):
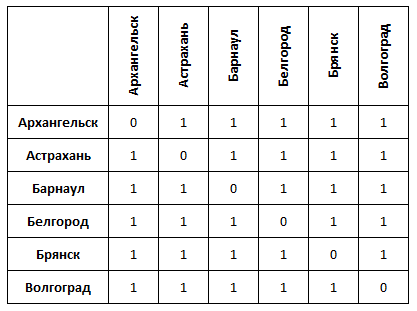
It is easy to imagine a matrix with abstract points, but with specific cities it is already much more difficult, since we have a stable idea of a geographical map. How to create a visualization in which there is no idea about the distance and the relation of "closer-further", the base for the geometry? Let's try to draw a discrete space, starting from one point and adding points one after another at the same distance from all the others.
Visualization of a discrete space using a simplex
To begin with, imagine that our discrete space consists of only one point A. For example, this can be some state of the system. Since the point is only one, the system is constant, always in the state corresponding to point A. The image of this point on a two-dimensional plane is elementary (the corresponding distance table is shown next to it according to the definition of a discrete space):
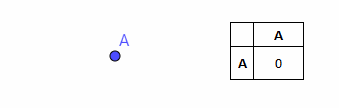
In such a space, no movements and changes are possible. We can say that such a space corresponds to the constant value of some variable.
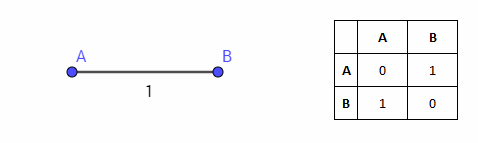
Add another point at a distance equal to 1. Two points are also easy to draw on the plane. Together with the distance between them, they form a segment AB:
Now we will try to draw on the plane another point, C. We should place it at a distance of 1 from points A and B, while maintaining the distance 1 and between these points. The set of points equidistant from this is a circle. If we construct two circles with unit radius and center at points A and B, then the intersection of these circles will give a set of points remote by one both from point A and from point B:
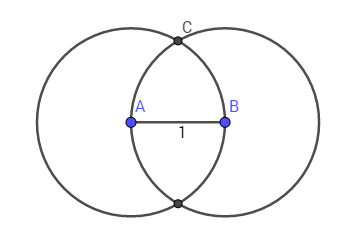
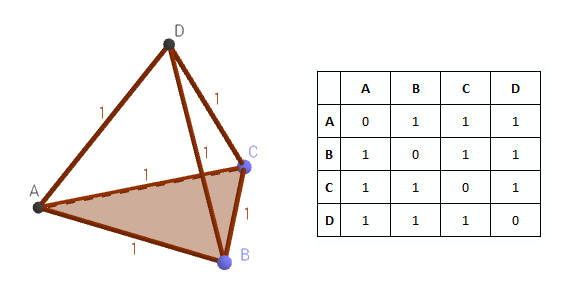
In the figure, one of the two intersection points of the circles is designated as C. The distance from point C to points A and B is equal to 1. Combining all three points, we obtain an equilateral triangle ABC:
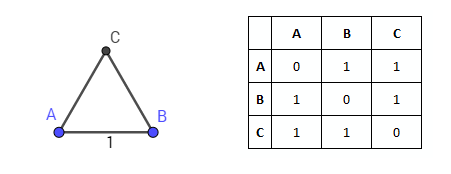
Thus, the discrete space of three points is visualized on the plane using a triangle. Add another point D. Is it possible to build this point so that the other three points are located at the same distance from it, equal to 1? To do this, two conditions must be met:
- Three points A, B and C must lie on a circle drawn from point D
- The radius of this circle must be 1
The first condition is satisfied, since a circle can be described around a regular triangle:
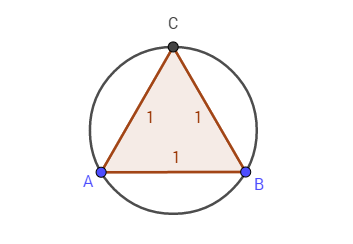
However, the radius of the circumcircle is:
 ,
,
where a is the side length. It turns out that the four points equidistant from each other can not be drawn on the plane. To fulfill the second condition, we have to move point D from the plane so that the distances to points A, B and C increase to 1. As a result, we get a regular tetrahedron, that is, a three-dimensional figure in space.
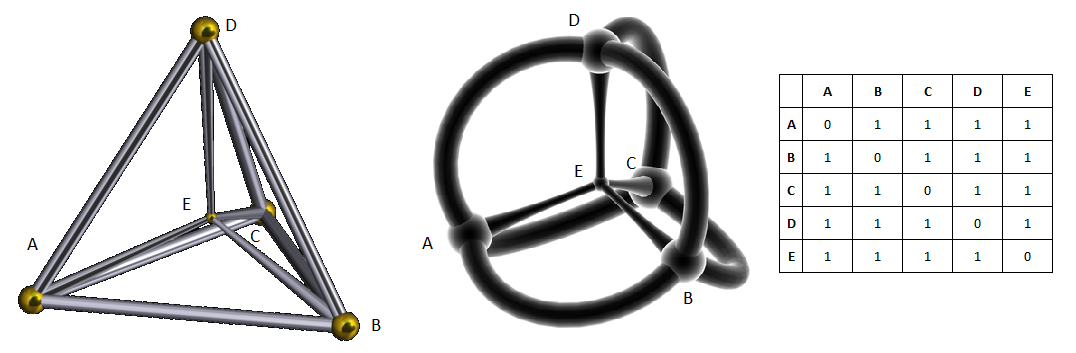
If we add another point to the discrete space, then we will again encounter a problem similar to adding the fourth point to the triangle. Now we will need to build a unit sphere on which four points A, B, C and D lie, in the center of which we place point E. The sphere will be described around a regular tetrahedron, but its radius will differ from unity:
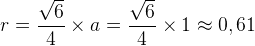
A figure in which five points are equidistant from each other is called a five-card reader (pentachor) . This is already a four-dimensional figure, the three-dimensional projection of which looks as follows (on the left is the Schlegel diagram, on the right is the stereographic projection, Wikipedia):
The generalization of all the figures we constructed, starting from a point, is an n -simplex — the simplest n- dimensional polytope with n + 1 vertices:
- point A: 0-simplex with one vertex (a point is an object with a zero-dimensional object)
- segment AB: 1-simplex with two vertices
- an equilateral triangle ABC: 2-simplex with three equidistant vertices
- regular tetrahedron ABCD: 3-simplex with four vertices
- fivefold ABCDE: 4-simplex with five vertices
- etc.
The first three simplexes are visualized on the plane as is. The tetrahedron can be projected onto a plane or make it a 3D model without distortion. A pentachor can be projected onto a plane with preservation of combinatorial properties or a 3D model can be made with distortions. 6-simplex and simplices of higher dimension can be represented as flat projections that preserve combinatorial properties, but it will not be possible to achieve greater clarity.
Thus, direct visualization of a discrete space with a large number of points in two or three dimensions, with which our visualization is limited, is difficult. Let us try to find some variant of the image of a discrete space with preservation of its essential properties, at least in some volume.
Thor as 3D visualization of discrete space
So far, we have looked at visualization of a discrete space as if from the outside, representing all points of the space in front of us, for example, on a computer screen. At the same time, visualization of the space was achieved, with a maximum of 4-5 points. What if we put an observer in one of the points of space, for example, point A? Then all the other points, no matter how many, will be equidistant from the selected point and will be located on a circle of unit radius:
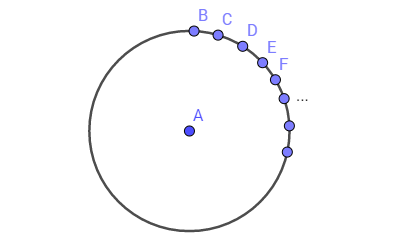
If there are infinitely many points of a discrete space, then their visualization from any chosen point of this space will be a circle. We found an interesting feature of discrete space. If we are outside of it, then in order to present it we need N - 1 measurements ( N is the number of points). But as soon as we find ourselves inside a discrete space, it is possible to construct its visualization in two dimensions, and this visualization is a unit circle.
A similar circle is built for any other point of a discrete space. If we do this, still being at point A, and representing another observer at other points, we get the following picture:
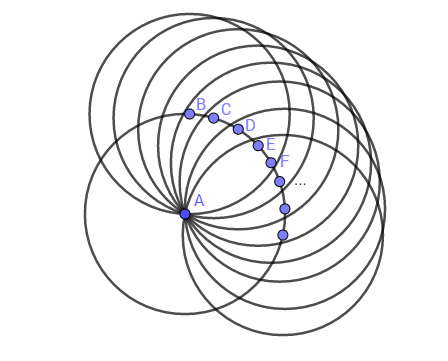
All circles constructed from points B, C and so on intersect at point A. That is, the visualization of the discrete space for observers at these points includes this point A.
However, the visualization obtained by us is not very visual with a large number of points. We will activate the third dimension - rotate all the circles, with the exception of the original one, by 90 degrees as follows (point A is located at the origin of coordinates):
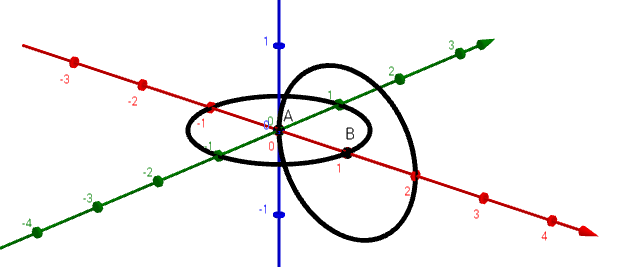
As a result, we get a closed (self-contacting) torus as 3D visualization of a discrete space:
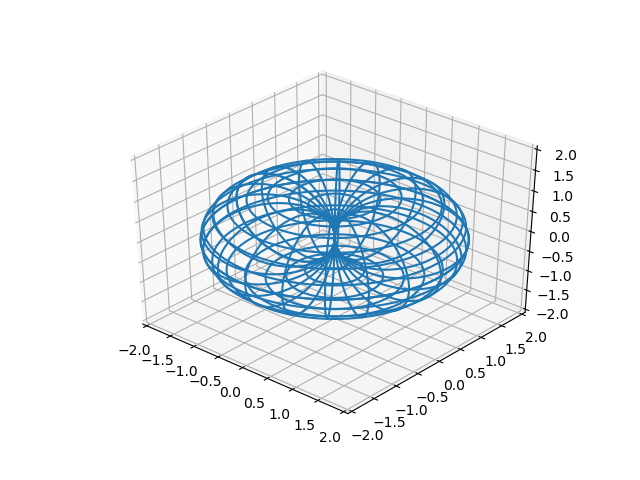
The resulting visualization implies that the observer is at one of the points in this space and imagines observers at other points in space. Also, the visualization of a discrete space with the help of a torus takes into account only the relationship between the point where the observer is located and other points, but not between arbitrary points.
findings
- The dimension of the visualization does not always coincide with the dimension of the rendered data or objects (dimensionless space and infinite-dimensional visualization)
- You can find forms of 3D graphics for data and other objects with dimensions greater than three, up to infinite
- The dimension of visualization "from the side" (outside of the object being visualized) may differ from the dimension of visualization from the inside (from any point of the object)
')
Source: https://habr.com/ru/post/346332/
All Articles